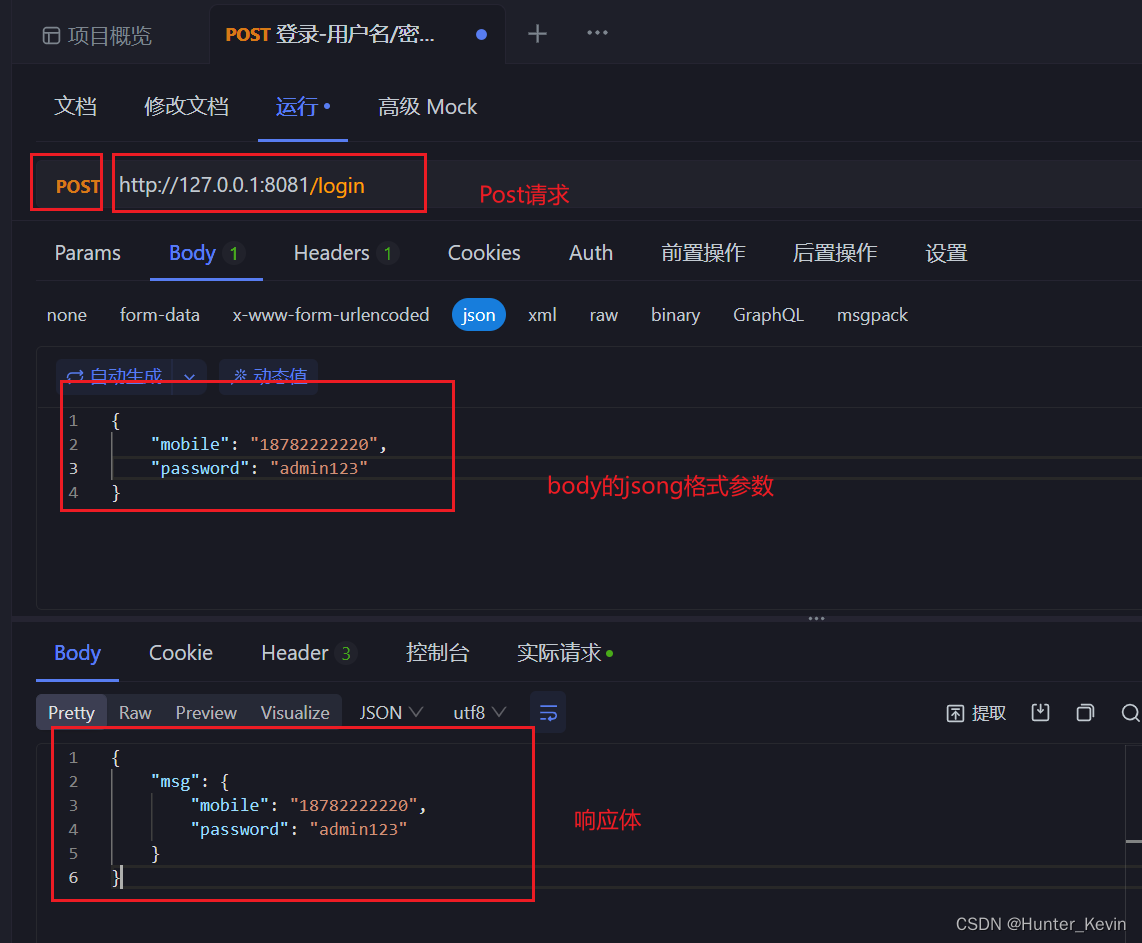
轮转数组

思路一
创建一个新内存空间,将需轮转的数依次放入,之后在把其它数放入
代码:
void rotate(int* nums, int numsSize, int k) {
k = k % numsSize;// 确定有效的旋转次数
if(k == 0)
return;
int* newnums = (int*)malloc(sizeof(int) * numsSize);//临时数组
//复制需要旋转的元素
int i;
for(i = 0;i < k;i++)
{
newnums[i] = nums[numsSize - k + i];
}
//复制不需要旋转的元素
for(i = 0;i<numsSize - k;i++)
{
newnums[k + i] = nums[i];
}
//拷贝至原数组
memmove(nums,newnums,sizeof(int) * numsSize);
}思路二
三段逆置,这个方法比较不容易想到具体为:

第一段 先把需要旋转的元素逆置
第二段 再把不需要旋转的元素逆置
第三段 最后再把整体逆置
这样子就可以很好的完成题目的需求了
代码:
void nizhi(int *arr,int numssize){
int left = 0;
int right = numssize - 1;
while(left < right)
{
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
}
void rotate(int* nums, int numsSize, int k) {
k = k % numsSize;// 确定有效的旋转次数
if(k == 0)
return;
//第一端 逆置
nizhi(nums + (numsSize - k),k);
//第二段 逆置
nizhi(nums,numsSize - k);
//第三段逆置
nizhi(nums,numsSize);
}消失的数字

思路一
将 0 - n 的数全部加起来,再把数数组中的元素全部减去,剩下的那个数字就是消失的数字
例如:

代码:
int missingNumber(int* nums, int numsSize){
//等差数列算出总和
int ret = numsSize*(1+numsSize)/2;
int count = 0;
//把数组中的数全部加起来
for(int i = 0;i<numsSize;i++)
{
count += nums[i];
}
//拿总数减去数组中的数,得到的就是消失的数字
return ret - count;
}思路二:
使用位的运算,将 0 ~ n 的数,全部与数组内的数进行 (按位异或) ^ 运算 留下来的数就是缺失的
原理:
任何数都等于 ^ 0 = 自己 例如 :001010 ^ 000000 = 001010
任何数 ^ 任何数 = 0 例如 :001010 ^ 001010 = 000000
知道了这个结论我们再将它带入实际例子中

我们发现两两成对的都被消除了,剩下的那个就是缺少的数字了
注意:0 ^ 0 ^1 ^ 1 ^ 2 ^ 2 ^ 3 ^ 3 ^ 5 ^ 5 ^ 4 它们打乱顺序对最终结果也不影响
像 1 + 1+ 2 = 4 || 2 + 1 + 1 = 4一样没有区别
代码:
int missingNumber(int* nums, int numsSize){
int find = 0;
for(int i = 0;i < numsSize;i++) //先把数组的数字 ^ 完
{
find ^= nums[i];
}
for(int i = 0;i <= numsSize;i++)//再把 0~ numsSize 的数字 ^ 完
{
find ^= i;
}
return find;
}或
int missingNumber(int* nums, int numsSize){
int find = 0;
for(int i = 0;i < numsSize;i++)//通过i访问素组所有元素
{
find ^= nums[i] ^ (i + 1); //i + 1 作为 1 ~ numsSize 去^ ,因为下标是从0开始的
}
return find;
}