EAAI 2023
paper
Intro
model-free的离线强化学习由于价值函数估计问题存在训练的稳定性以及鲁棒性较低。本文提出基于模型的方法,同构构建稳定的动力学模型帮助策略的稳定训练。
method
本文基于模型的方法,所构造的转移模型输入状态动作,输出的状态差异
Δ
s
=
s
t
+
1
−
s
t
\Delta s=s_{t+1}-s_{t}
Δs=st+1−st而非直接预测下一状态值。
L
(
ϕ
)
=
∑
t
∥
f
ϕ
(
s
t
,
a
t
)
−
(
s
t
+
1
−
s
t
)
−
μ
Δ
s
σ
Δ
s
∥
2
L(\phi)=\sum_{t}\|f_{\phi}(s_{t},a_{t})-\frac{(s_{t+1}-s_{t})-\mu^{\Delta\mathbf{s}}}{\sigma^{\Delta\mathbf{s}}}\|_{2}
L(ϕ)=t∑∥fϕ(st,at)−σΔs(st+1−st)−μΔs∥2
文章假设转移误差符合分布
(
s
′
−
s
′
^
)
∼
N
(
0
,
−
log
p
e
,
β
(
s
,
a
)
)
(s'-\hat{s'})\sim\mathcal{N}(0,-\log p_{e,\beta}(s,a))
(s′−s′^)∼N(0,−logpe,β(s,a))。最小化模型误差的等价于如下
argmin
θ
E
[
(
s
′
−
s
′
^
)
2
]
=
argmin
θ
E
[
−
log
p
e
,
β
(
s
^
,
a
^
)
]
=
argmax
θ
E
[
p
e
,
β
(
s
^
,
a
^
)
]
=
argmax
θ
E
[
μ
β
e
(
s
^
)
β
(
a
^
∣
s
^
)
]
\begin{aligned}&\quad\underset{\theta}{\operatorname*{argmin}}\mathbb{E}[(s^{\prime}-\hat{s^{\prime}})^{2}]\\&=\quad\underset{\theta}{\operatorname*{argmin}}\mathbb{E}[-\log p_{e,\beta}(\hat{s},\hat{a})]\\&=\quad\underset{\theta}{\operatorname*{argmax}}\mathbb{E}[p_{e,\beta}(\hat{s},\hat{a})]\\&=\quad\underset{\theta}{\operatorname*{argmax}}\quad\mathbb{E}[\mu_{\beta}^{e}(\hat{s})\beta(\hat{a}|\hat{s})]\end{aligned}
θargminE[(s′−s′^)2]=θargminE[−logpe,β(s^,a^)]=θargmaxE[pe,β(s^,a^)]=θargmaxE[μβe(s^)β(a^∣s^)]
进一步,文章利用一个VAE近似
μ
β
e
(
s
^
)
β
(
a
^
∣
s
^
)
\mu_{\beta}^{e}(\hat{s})\beta(\hat{a}|\hat{s})
μβe(s^)β(a^∣s^),通过最小化ELBO实现参数优化
L
(
ω
)
=
E
q
ω
(
z
∣
s
,
a
)
[
−
log
p
ω
(
s
,
a
∣
z
)
]
+
D
K
L
(
q
ω
(
z
∣
s
,
a
)
∣
∣
p
(
z
)
)
p
(
z
)
∼
N
(
0
,
1
)
L(\omega)=\mathbb{E}_{q_{\omega}(z|s,a)}[-\log p_{\omega}(s,a|z)]+D_{KL}(q_{\omega}(z|s,a)||p(z))\\p(z)\sim\mathcal{N}(0,1)
L(ω)=Eqω(z∣s,a)[−logpω(s,a∣z)]+DKL(qω(z∣s,a)∣∣p(z))p(z)∼N(0,1)
然后通过最小化累计负对数似然,利用该模型限制策略以产生让模型偏差最小化的样本
E
[
P
]
=
∑
t
E
q
ω
(
z
∣
s
,
a
)
,
(
s
,
a
)
∼
π
,
f
[
−
log
p
ω
(
s
,
a
∣
z
)
]
\mathbb{E}[P]=\sum_t\mathbb{E}_{q_\omega(z|s,a),(s,a)\sim\pi,f}[-\log p_\omega(s,a|z)]
E[P]=t∑Eqω(z∣s,a),(s,a)∼π,f[−logpω(s,a∣z)]
同时,基于离线数据构建集成模型预测奖励函数,使得确定性策略下的模型预测结果为保守的估计
E
[
R
]
=
η
min
k
{
∑
t
γ
t
r
(
s
t
,
π
θ
(
s
t
)
,
f
k
(
s
t
,
π
θ
(
s
t
)
)
)
}
+
(
1
−
η
)
1
K
∑
k
[
∑
t
γ
t
r
(
s
t
,
π
θ
(
s
t
)
,
f
k
(
s
t
,
π
θ
(
s
t
)
)
)
]
\mathbb{E}[R]=\eta\min_k\left\{\sum_t\gamma^tr(s_t,\pi_\theta(s_t),f_k(s_t,\pi_\theta(s_t)))\right\}\\+(1-\eta)\frac1K\sum_k\left[\sum_t\gamma^tr(s_t,\pi_\theta(s_t),f_k(s_t,\pi_\theta(s_t)))\right]
E[R]=ηkmin{t∑γtr(st,πθ(st),fk(st,πθ(st)))}+(1−η)K1k∑[t∑γtr(st,πθ(st),fk(st,πθ(st)))]
奖励模型与状态转移模型联合作为正则化项优化策略:
L
(
θ
)
=
−
λ
E
[
R
]
+
(
1
−
λ
)
E
[
P
]
L(\theta)=-\lambda\mathbb{E}[R]+(1-\lambda)\mathbb{E}[P]
L(θ)=−λE[R]+(1−λ)E[P]
伪代码






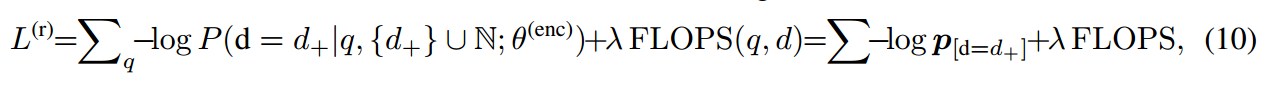
![[算法][单调栈] [leetcode]316. 去除重复字母](https://img-blog.csdnimg.cn/direct/8c8d9331903e41c1a467a886fda7cb2e.gif#pic_center)