Leetcode刷题Day24-------------------回溯算法

1. 理论基础

• 题目链接/文章讲解：https://programmercarl.com/%E5%9B%9E%E6%BA%AF%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
• 视频讲解：https://www.bilibili.com/video/BV1cy4y167mM

回溯算法涉及递归，是一种纯暴力搜索的算法
组合（12 和21是一种）、切割、子集、排序（12 和21是2种）、棋盘（N皇后）

回溯算法解题模版：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

2. 77. 组合

• 题目链接：https://leetcode.cn/problems/combinations/
• 文章讲解：https://programmercarl.com/0077.%E7%BB%84%E5%90%88.html
• 视频讲解：https://www.bilibili.com/video/BV1ti4y1L7cv
• 剪枝操作：https://www.bilibili.com/video/BV1wi4y157er

二维数组是最终的结果
一维数据是单次取到的结果

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    //官方函数
    public List<List<Integer>> combine(int n, int k) {
        backTracking(n,k,1);
        return result;
    }
    //递归函数
    public void backTracking(int n, int k, int startIndex){
        if(path.size()==k) {
            result.add(new ArrayList<>(path));//把得到的path收集到结果中
            return;
        }
        
        //for(int i=startIndex;i<=n;i++){
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { //优化的地方、剪枝操作
            path.add(i);//把第一个数加到path里
            backTracking(n,k,i+1);//取path里的第二个数，第三个数，第四个...
            path.removeLast();//删掉path里的最后一个数，回溯
        }
    }   
}

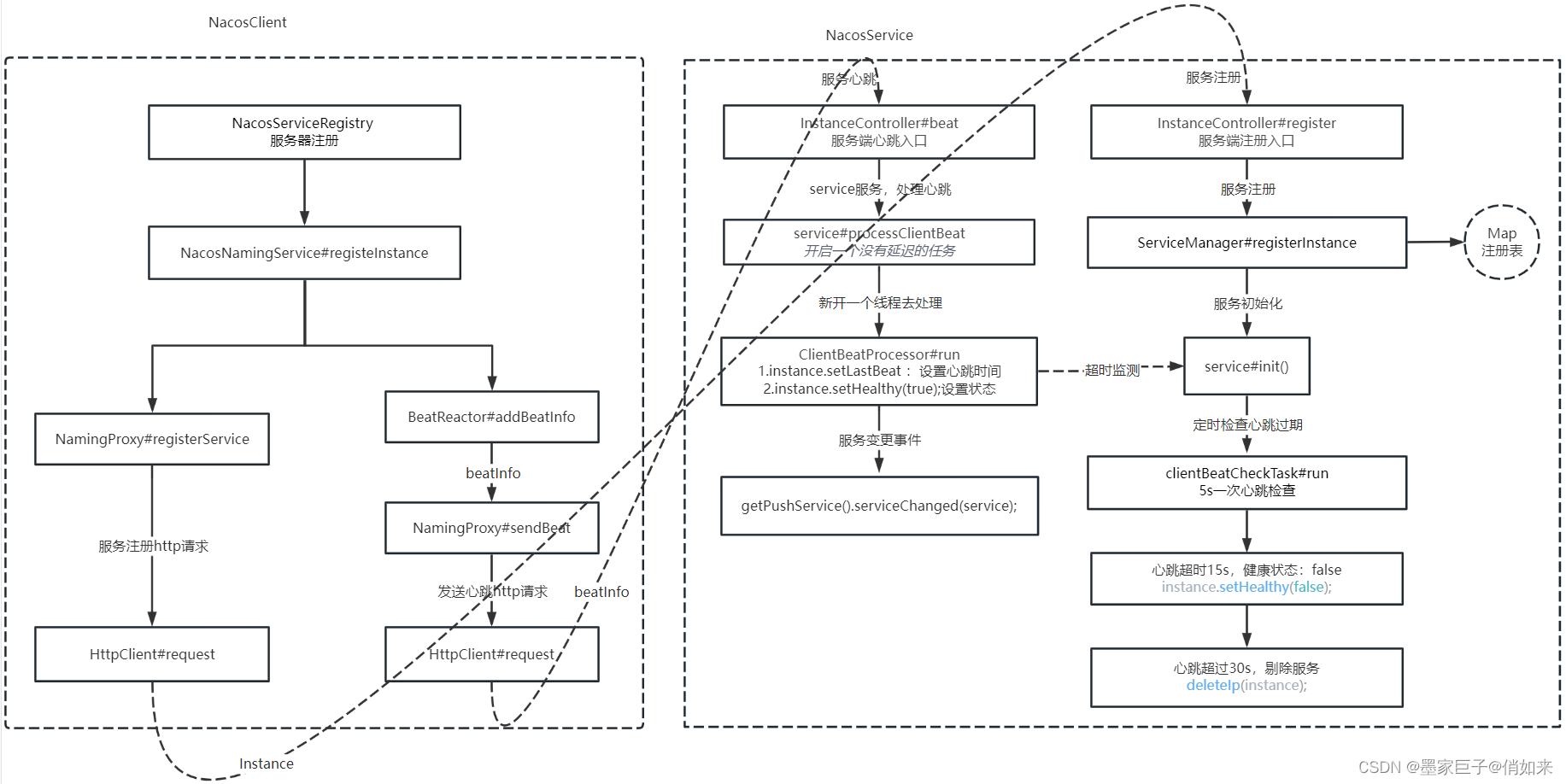
剪枝操作详解：

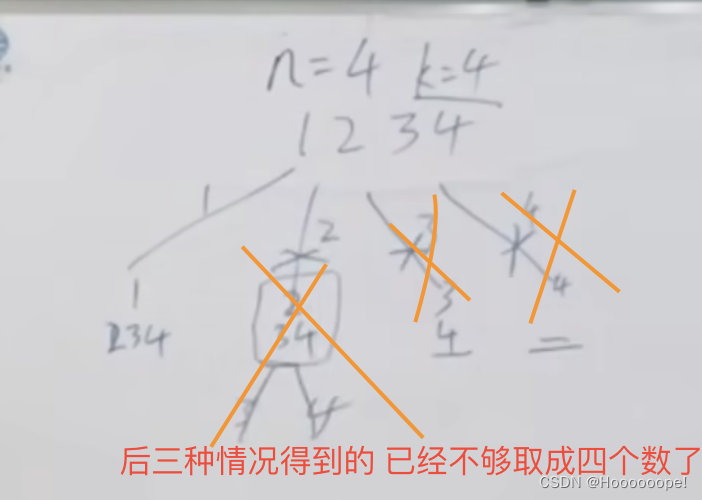
（该图来自B站算法随想录视频中的截图）
剪枝后的循环条件：for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { //优化的地方、剪枝操作

语句积累

	List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    path.removeLast();//删掉path里的最后一个数，回溯