【算法】滑动窗口——将x减到0的最小操作数

news2025/1/13 10:23:30

本节博客主要是讲的我解“将x减到0的最小操作数”这道题的思路历程，从最开始的想法到代码提交的详细记录，有需要借鉴即可。

1.题目

题目链接：LINK
在这里插入图片描述
看题目意思是就是给你一个数X，让你拿着数组中的最左边或者最右边的数字与这个数字抵消(相减)，直到X为0，或者找不到，如果可以抵消掉，记录拿这个数组中最少的一个数字个数，而且用数组中的值的时候，必须用两头的。

这个暴力求解…都不知道下一次是用左边的数字还是右边的数字，…，基本暴力解法就想不到了。

这里我们老师讲的，说要用到转换思想——“正难则反”
什么意思呢？
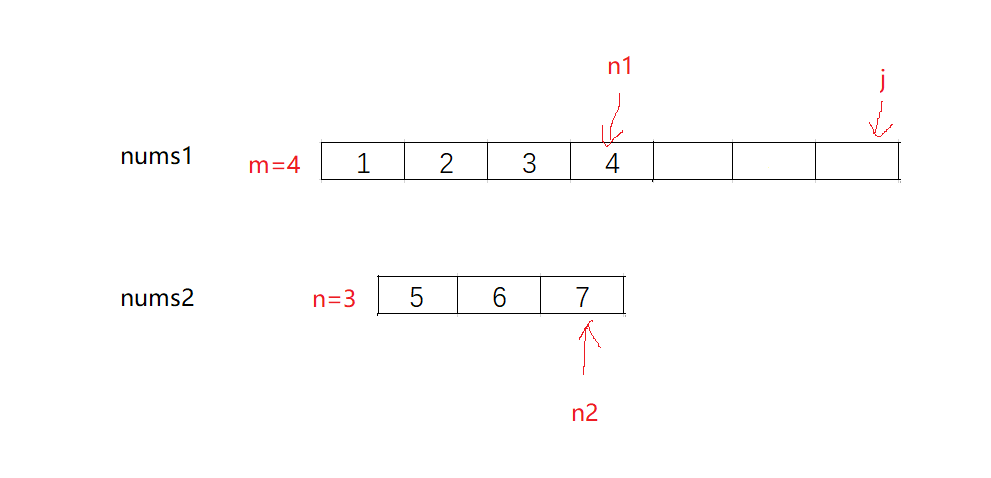
其实对于这个题目来说，整个数组可以分为三块，即下图：
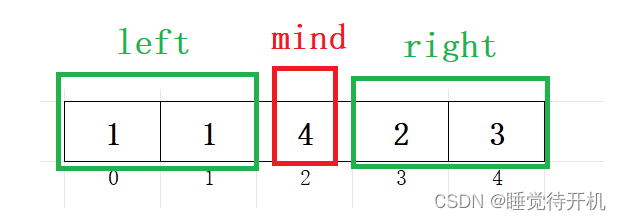
在这里插入图片描述
说白了就让我们找left + right这两块中最小的数字个数
那可以等效于让我们找 该数组总数字个数 - mind最大数字个数

顺着前面“滑动窗口”的代码思路：
大体就可以写出下面代码：

2.代码示例

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int ALsum = 0;
        int n = nums.size();
        for(size_t i = 0;i<n;i++)
        {
            ALsum+=nums[i];
        }
        long long target = ALsum - x;//中间的目标值，满足目标值就进行更新结果
        int ret = -1;//代表两边的长度，取最小值
        int len = 0;//代表left和right之间的长度，取最大值
        long long sum = 0;//代表中间区间的和

        //处理特殊情况
        if (sum == target)
        {
            return n;
        }

        for(int right = 0,left = 0; right < n; right++)
        {
            
            //进窗口
            sum+=nums[right];

            //出窗口
            while(sum > target && left < right)
            {
                sum-=nums[left];
                left++;
            }

            //更新结果
            if(sum == target)
            {
                len = max(len,right - left + 1);
            }
        }

        return ret = len == 0 ? -1 : n - len;
    }
};

这个题做完之后感觉还是有一两个坑的，下面进行展示：

3.细节

3.1left越界

这个问题呢，也可以说是X > 整个数组之和，即target小于0，导致了left会不断右移的情况：
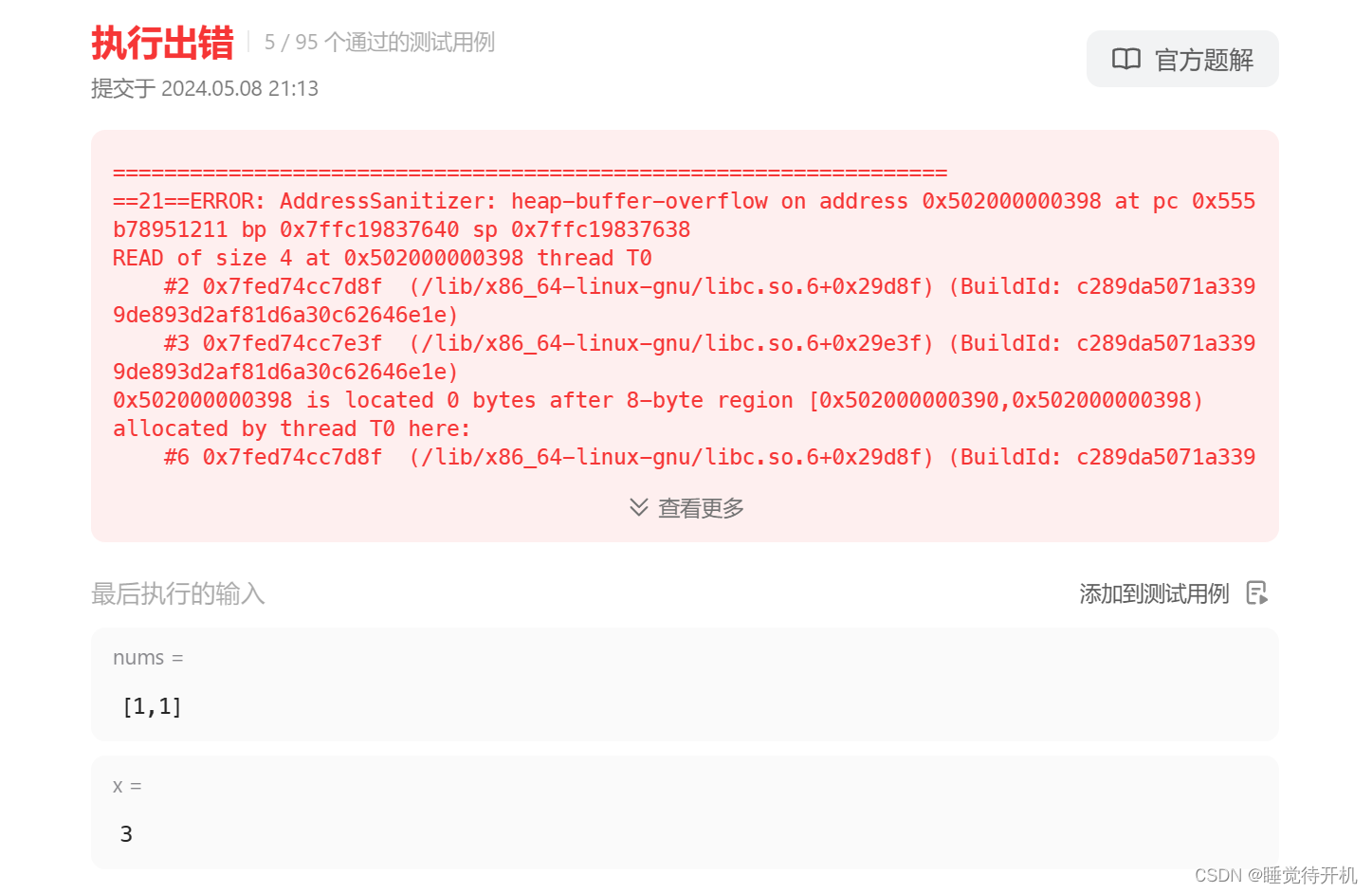
在这里插入图片描述

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int ALsum = 0;
        int n = nums.size();
        for(size_t i = 0;i<n;i++)
        {
            ALsum+=nums[i];
        }
        int target = ALsum - x;//中间的目标值，满足目标值就进行更新结果
        int ret = -1;//代表两边的长度，取最小值
        int len = 0;//代表left和right之间的长度，取最大值
        int sum = 0;//代表中间区间的和

        for(int right = 0,left = 0; right < n; right++)
        {
            //进窗口
            sum+=nums[right];

            //出窗口
            while(sum > target)
            {
                sum-=nums[left];
                left++;
            }

            //更新结果
            if(sum == target)
            {
                len = max(len,right - left + 1);
            }
        }

        return ret = len == 0 ? -1 : n - len;
    }
};

这个主要是越界问题，是left越界了。

3.2特殊情况

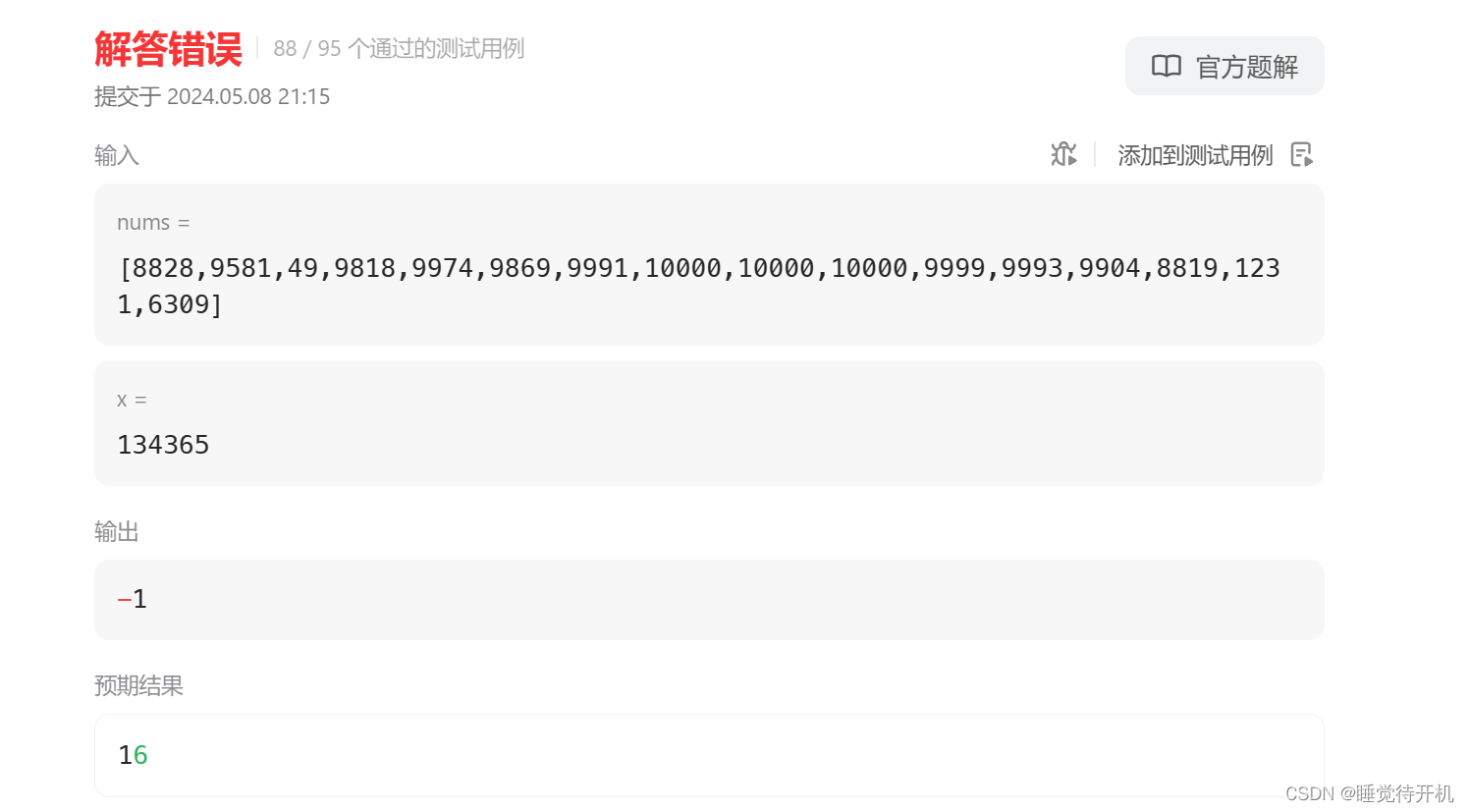
在这里插入图片描述

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int ALsum = 0;
        int n = nums.size();
        for(size_t i = 0;i<n;i++)
        {
            ALsum+=nums[i];
        }
        int target = ALsum - x;//中间的目标值，满足目标值就进行更新结果
        int ret = -1;//代表两边的长度，取最小值
        int len = 0;//代表left和right之间的长度，取最大值
        int sum = 0;//代表中间区间的和

        for(int right = 0,left = 0; right < n; right++)
        {
            //进窗口
            sum+=nums[right];

            //出窗口
            while(sum > target && left < right)
            {
                sum-=nums[left];
                left++;
            }

            //更新结果
            if(sum == target)
            {
                len = max(len,right - left + 1);
            }
        }

        return ret = len == 0 ? -1 : n - len;
    }
};