哈希表的基本思路是通过某种方式将某个值映射到对应的位置,这里的采取的方式是除留余数法,即将原本的值取模以后再存入到数组的对应下标,即便存入的值是一个字符串,也可以根据字符串哈希算法将字符串转换成对应的ASCII码值,然后再取模。
如果某个位置已经存了其他数据,相互冲突的数据拉成一个链表,哈希表中存放第一个结点的地址。我们把这种方法称为 开散列(或者哈希桶)。

目录
1、基本思路
2、极端情况的处理
3、数据存储的结构
4、 查找实现
5、插入实现
6、移除实现
1、基本思路
如果某个位置已经存了其他数据,直接头插当前位置对应的链表,之所以选择头插,是因为哈希表中只保存头结点的地址,尾插的话需要从头遍历当前链表。
2、极端情况的处理
开散列法存在一些极端情况,比如:
- 1、存了50个值,有40个值是冲突的,挂在一个桶下面
- 2、存了10000个值,平均每个桶长度是100,极端场景有些桶可能有上千个结点,此时的查找效率没有特别明显的提升
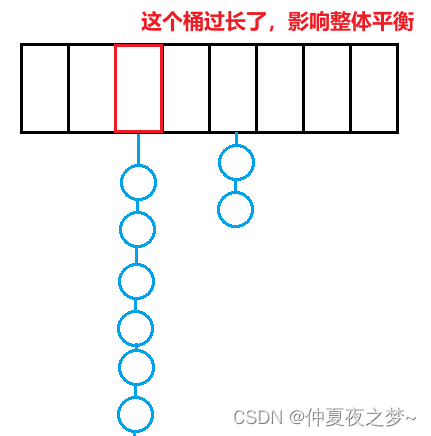
解决这种极端情况的关键就是扩容。有两种情况需要考虑扩容:
- 哈希表的负载因子大于0.75,就扩容。(负载因子 = 有效数据个数 / 哈希表容量 ) —— 减少冲突
- 当一个桶下的结点个数超过 10 个时,就扩容。(最大结点数可以自己决定)—— 避免桶过长
拓展:JDK8以后采用了一种更新的方式,当一个桶长度超过一定值以后,转换成红黑树(JAVA中每个桶下面超过8个就转换成红黑树)
3、数据存储的结构
哈希表中每个位置保存链表头结点的地址,数据结构的定义如下:
template <class T>
struct HashNode
{
T _data; // 保存的数据
HashNode<T> *_next; // 下一个结点的地址
HashNode(const T &data)
: _data(data), _next(nullptr)
{
}
};
4、 查找实现
首先通过 key 值算出保存到哈希表的哪个桶下,即保存到数组中的哪个下标位置,然后去遍历该位置的链表。
Node *Find(const K &key)
{
if (_tables.empty())
{
return nullptr;
}
HashFunc hf; // hf 是为了将字符串类型或者自定义类型转换成无符号整型的仿函数
size_t index = hf(key) % _tables.size();
Node *cur = _tables[index];
KeyOfT kot; // kot 是为了兼容键值对 和 单一数据的存储
while (cur)
{
if (kot(cur->_data) == key)
{
return cur;
}
else
{
cur = cur->_next;
}
}
return nullptr;
}
5、插入实现
第一步,检查插入的数据在哈希表中是否存在。目的是为了去重。
第二步,检查是否需要扩容。如果需要扩容,遍历原本哈希表中的每一个结点,重新计算映射下标,复用原来的结点,直接挂载到对应的桶下面。
第三步,插入新的结点。
注意:扩容时不推荐使用递归。递归时默认会重新创建新的结点,明明有原本的结点可以用,还要去创建新的结点,就会造成空间浪费。
bool Insert(const T &data)
{
KeyOfT kot;
Node *ret = Find(kot(data)); // 先判断要插入的数据是否存在,目的是为了去重
if (ret)
return false;
HashFunc hf;
// 负载因子 == 1时扩容
if (_n == _tables.size())
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node *> newTables;
newTables.resize(newSize);
// 遍历之前的哈希表,根据新的容量大小重新每个数据的映射(这里复用原来的结点)
for (size_t i = 0; i < _tables.size(); ++i)
{
Node *cur = _tables[i];
while (cur)
{
Node *next = cur->_next;
size_t index = hf(kot(cur->_data)) % newTables.size();
// 头插
cur->_next = newTables[index];
newTables[index] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
size_t index = hf(kot(data)) % _tables.size();
Node *newnode = new Node(data);
// 头插
newnode->_next = _tables[index];
_tables[index] = newnode;
++_n; // 有效数据个数自增
return true;
}
6、移除实现
先根据 key 值确定要删除的结点在哪个桶下面,然后再开始遍历该桶下的链表结点。移除时需要考虑被删除的结点在当前链表中的位置,头删 or 中间删除。
bool Erase(const K &key)
{
if (_tables.empty())
{
return false;
}
HashFunc hf;
size_t index = hf(key) % _tables.size();
Node *prev = nullptr;
Node *cur = _tables[index];
KeyOfT kot;
while (cur)
{
if (kot(cur->_data) == key)
{
if (prev == nullptr) // 头删
{
_tables[index] = cur->_next;
}
else // 中间删除
{
prev->_next = cur->_next;
}
--_n;
delete cur;
return true;
}
else
{
prev = cur;
cur = cur->_next;
}
}
return false;
}