曲线积分
第一类曲线积分:对弧长的积分计算方法
定理:设
f
(
x
,
y
)
f(x,y)
f(x,y)在曲线弧
L
L
L上有定义且连续,
L
L
L的参数方程是
{
x
=
φ
(
t
)
y
=
ψ
(
t
)
(
α
≤
t
≤
β
)
\begin{cases} x=\varphi(t)\\ y=\psi(t) \end{cases}(\alpha\le t\le\beta)
{x=φ(t)y=ψ(t)(α≤t≤β)
若
φ
(
t
)
,
ψ
(
t
)
\varphi(t),\psi(t)
φ(t),ψ(t)在
[
α
,
β
]
[\alpha, \beta]
[α,β]上具有连续的一阶偏导数,且
φ
′
2
(
t
)
+
ψ
′
2
(
t
)
≠
0
\varphi'^2(t)+\psi'^2(t)\ne0
φ′2(t)+ψ′2(t)=0,则曲线积分
∫
L
f
(
x
,
y
)
d
s
\int_Lf(x,y)ds
∫Lf(x,y)ds存在,且
∫
L
f
(
x
,
y
)
d
s
=
∫
α
β
f
(
φ
(
t
)
,
ψ
(
t
)
)
φ
′
2
(
t
)
+
ψ
′
2
(
t
)
d
t
(
α
≤
β
)
\int_Lf(x,y)ds=\int_\alpha^\beta f(\varphi(t),\psi(t))\sqrt{\varphi'^2(t)+\psi'^2(t)}dt(\alpha\le \beta)
∫Lf(x,y)ds=∫αβf(φ(t),ψ(t))φ′2(t)+ψ′2(t)dt(α≤β)
参数方程的一个特例是
{
x
=
x
y
=
y
(
x
)
(
α
≤
x
≤
β
)
\begin{cases} x=x\\ y=y(x) \end{cases}(\alpha\le x\le\beta)
{x=xy=y(x)(α≤x≤β)
第二类曲线积分:沿坐标轴进行积分
考虑一个变力做功的场景:变力为
F
(
x
,
y
)
=
P
(
x
,
y
)
i
+
Q
(
x
,
y
)
j
\bold F(x,y)=P(x,y)\bold i+Q(x,y)\bold j
F(x,y)=P(x,y)i+Q(x,y)j,沿着曲线做功
∫
L
F
(
x
,
y
)
d
r
=
∫
L
P
(
x
,
y
)
d
x
+
∫
L
Q
(
x
,
y
)
d
y
\int_L\bold F(x,y)d\bold r=\int_LP(x,y)dx+\int_LQ(x,y)dy
∫LF(x,y)dr=∫LP(x,y)dx+∫LQ(x,y)dy其中
F
(
x
,
y
)
=
P
(
x
,
y
)
i
+
Q
(
x
,
y
)
j
,
d
r
=
d
x
i
+
d
y
j
\bold F(x,y)=P(x,y)\bold i+Q(x,y)\bold j, d\bold r=dx\bold i+dy\bold j
F(x,y)=P(x,y)i+Q(x,y)j,dr=dxi+dyj
两类曲线积分的关系
∫
L
P
(
x
,
y
)
d
x
+
Q
(
x
,
y
)
d
y
=
∫
L
P
(
x
,
y
)
cos
α
+
Q
(
x
,
y
)
cos
β
d
s
\int_LP(x,y)dx+Q(x,y)dy=\int_LP(x,y)\cos\alpha+Q(x,y)\cos\beta ds
∫LP(x,y)dx+Q(x,y)dy=∫LP(x,y)cosα+Q(x,y)cosβds其中
α
,
β
\alpha, \beta
α,β是有向曲线在
(
x
,
y
)
(x,y)
(x,y)处的方向角(和坐标轴的夹角)。
推导
假设
x
,
y
x,y
x,y满足参数方程
{
x
(
t
)
=
φ
(
t
)
y
(
t
)
=
ψ
(
t
)
\begin{aligned} \begin{cases} x(t)&=\varphi(t)\\ y(t)&=\psi(t) \end{cases} \end{aligned}
{x(t)y(t)=φ(t)=ψ(t)
对于第二类曲线积分
I
=
∫
P
(
x
,
y
)
d
x
+
∫
Q
(
x
,
y
)
d
y
=
∫
a
b
P
(
φ
(
t
)
,
ψ
(
t
)
)
φ
′
(
t
)
d
t
+
∫
a
b
Q
(
φ
(
t
)
,
ψ
(
t
)
)
ψ
′
(
t
)
d
t
\begin{aligned} I&=\int P(x,y)dx+\int Q(x,y)dy\\ &=\int_a^b P(\varphi(t),\psi(t))\varphi'(t)dt+\int_a^b Q(\varphi(t),\psi(t))\psi'(t)dt \end{aligned}
I=∫P(x,y)dx+∫Q(x,y)dy=∫abP(φ(t),ψ(t))φ′(t)dt+∫abQ(φ(t),ψ(t))ψ′(t)dt
考虑曲线在
(
x
,
y
)
(x,y)
(x,y)的切线方向向量
τ
=
φ
′
(
t
)
i
+
ψ
′
(
t
)
j
\bold\tau=\varphi'(t)\bold i+\psi'(t)\bold j
τ=φ′(t)i+ψ′(t)j
则其两个方向角
cos
α
=
φ
′
(
t
)
φ
′
(
t
)
2
+
ψ
′
(
t
)
2
cos
β
=
ψ
′
(
t
)
φ
′
(
t
)
2
+
ψ
′
(
t
)
2
\cos\alpha = \frac{\varphi'(t)}{\sqrt{\varphi'(t)^2+\psi'(t)^2}}\\ \cos\beta = \frac{\psi'(t)}{\sqrt{\varphi'(t)^2+\psi'(t)^2}}\
cosα=φ′(t)2+ψ′(t)2φ′(t)cosβ=φ′(t)2+ψ′(t)2ψ′(t)
考虑下面函数的第一类曲线积分
I
′
=
∫
P
(
x
,
y
)
cos
α
+
Q
(
x
,
y
)
cos
β
d
s
=
∫
P
(
φ
(
t
)
,
ψ
(
t
)
)
φ
′
(
t
)
φ
′
(
t
)
2
+
ψ
′
(
t
)
2
+
∫
Q
(
φ
(
t
)
,
ψ
(
t
)
)
ψ
′
(
t
)
φ
′
(
t
)
2
+
ψ
′
(
t
)
2
d
s
=
∫
(
P
(
φ
(
t
)
,
ψ
(
t
)
)
φ
′
(
t
)
φ
′
(
t
)
2
+
ψ
′
(
t
)
2
+
∫
Q
(
φ
(
t
)
,
ψ
(
t
)
)
ψ
′
(
t
)
φ
′
(
t
)
2
+
ψ
′
(
t
)
2
)
φ
′
(
t
)
2
+
ψ
′
(
t
)
2
d
t
=
∫
P
(
φ
(
t
)
,
ψ
(
t
)
)
φ
′
(
t
)
+
∫
Q
(
φ
(
t
)
,
ψ
(
t
)
)
ψ
′
(
t
)
d
t
=
I
\begin{aligned} I' &= \int P(x,y)\cos\alpha+Q(x,y)\cos\beta ds\\ &=\int P(\varphi(t), \psi(t)) \frac{\varphi'(t)}{\sqrt{\varphi'(t)^2+\psi'(t)^2}} +\int Q(\varphi(t), \psi(t)) \frac{\psi'(t)}{\sqrt{\varphi'(t)^2+\psi'(t)^2}} ds\\ &=\int \left (P(\varphi(t), \psi(t)) \frac{\varphi'(t)}{\sqrt{\varphi'(t)^2+\psi'(t)^2}} +\int Q(\varphi(t), \psi(t)) \frac{\psi'(t)}{\sqrt{\varphi'(t)^2+\psi'(t)^2}} \right)\sqrt{\varphi'(t)^2+\psi'(t)^2}dt\\ &=\int P(\varphi(t), \psi(t)) \varphi'(t)+\int Q(\varphi(t), \psi(t)) \psi'(t)dt\\ &=I \end{aligned}
I′=∫P(x,y)cosα+Q(x,y)cosβds=∫P(φ(t),ψ(t))φ′(t)2+ψ′(t)2φ′(t)+∫Q(φ(t),ψ(t))φ′(t)2+ψ′(t)2ψ′(t)ds=∫(P(φ(t),ψ(t))φ′(t)2+ψ′(t)2φ′(t)+∫Q(φ(t),ψ(t))φ′(t)2+ψ′(t)2ψ′(t))φ′(t)2+ψ′(t)2dt=∫P(φ(t),ψ(t))φ′(t)+∫Q(φ(t),ψ(t))ψ′(t)dt=I
理解
怎么直观理解呢?让我们会到变力做功问题。按照定义,适合计算的场景是第二类曲线积分。但是实际上也可以使用第一类曲线积分来进行计算。也就是计算曲线上每一点做功的量。
x
x
x方向上每一点移动微小距离从
A
A
A到
B
B
B做功的量
W
x
=
P
(
x
,
y
)
i
→
⋅
τ
→
=
P
(
x
,
y
)
τ
cos
α
=
P
(
x
,
y
)
cos
α
τ
=
P
(
x
,
y
)
cos
α
d
s
\begin{aligned} W_x&=P(x,y)\overrightarrow{\bold i}\cdot\overrightarrow{\bold{\tau}}\\ &=P(x,y)\tau\cos{\alpha}\\ &=P(x,y)\cos{\alpha}\ \tau\\ &=P(x,y)\cos{\alpha}\ ds \end{aligned}
Wx=P(x,y)i⋅τ=P(x,y)τcosα=P(x,y)cosα τ=P(x,y)cosα ds
可以将此处的功看做
P
(
x
,
y
)
P(x,y)
P(x,y)在此处的线密度,
Q
(
x
,
y
)
Q(x,y)
Q(x,y)类似。其中
τ
→
\overrightarrow{\bold\tau}
τ是指向从
A
A
A指向
B
B
B的向量,当
A
A
A到
B
B
B距离很近时,也就是其切向量。第一类和第二类曲线积分关系理解的一个问题是,
P
(
x
,
y
)
P(x,y)
P(x,y)已经是
x
x
x轴分量了,为什么还需要乘
c
o
s
α
cos\alpha
cosα,这是因为为了计算其做功,需要使用其在路径方向上的分量来计算。就好比,为了计算做功,首先对力进行
x
y
xy
xy方向的正交分解,但是因为移动的方向和坐标轴也不垂直或平行,需要分别对两个分量在路径方向的分量上再次分解。另外一种理解方式是,这个
cos
α
\cos\alpha
cosα不是乘在
P
(
x
,
y
)
P(x,y)
P(x,y)上,而是乘在
d
s
ds
ds上,这种理解就是将路径也作了正交分解,然后和对应分量进行求积。
举个例子,计算恒力
F
(
x
,
y
)
=
−
i
+
j
F(x,y)=-\bold i+\bold j
F(x,y)=−i+j沿圆周
x
2
+
y
2
=
1
x^2+y^2=1
x2+y2=1从
(
1
,
0
)
(1,0)
(1,0)到
(
0
,
1
)
(0,1)
(0,1)做的功。根据根据高中知识(同时格林公式加以验证),恒力做功和路径无关,做的功为
W
=
F
s
=
2
⋅
2
=
2
J
W=Fs=\sqrt 2\cdot\sqrt 2=2J
W=Fs=2⋅2=2J
使用第二类曲线积分
W
=
∫
L
F
→
d
r
→
=
∫
1
0
P
(
x
,
y
)
d
x
+
∫
0
1
Q
(
x
,
y
)
d
y
=
2
\begin{aligned} W &=\int_L\overrightarrow{\bold F}d\overrightarrow{\bold r} \\ &=\int_{1}^{0}P(x,y)dx+\int_{0}^{1}Q(x,y)dy\\ &=2 \end{aligned}
W=∫LFdr=∫10P(x,y)dx+∫01Q(x,y)dy=2
使用第一类曲线积分,在任意一点
(
x
,
y
)
(x,y)
(x,y)
d
W
=
F
→
d
r
→
=
∣
F
→
∣
∣
d
r
→
∣
cos
α
(
α
是
F
→
(
−
1
,
1
)
和曲线切线
(
1
,
−
x
1
−
x
2
)
的夹角,不是方向角
)
=
∣
F
→
∣
cos
α
d
s
=
2
⋅
−
x
+
1
−
x
2
1
⋅
2
d
s
=
2
⋅
−
x
+
1
−
x
2
1
⋅
2
1
+
y
′
2
d
x
\begin{aligned} dW&=\overrightarrow{\bold F}d\overrightarrow{\bold r} \\ &=|\overrightarrow{\bold F}||d\overrightarrow{\bold r} |\cos\alpha(\alpha是\overrightarrow{\bold F}(-1,1)和曲线切线(1,\frac{-x}{\sqrt{1-x^2}})的夹角,不是方向角)\\ &=|\overrightarrow{\bold F}|\cos\alpha ds \\ &=\sqrt 2\cdot \frac{-x+\sqrt{1-x^2}}{1\cdot\sqrt 2}ds\\ &=\sqrt 2\cdot \frac{-x+\sqrt{1-x^2}}{1\cdot\sqrt 2}\sqrt{1+y'^2}dx \end{aligned}
dW=Fdr=∣F∣∣dr∣cosα(α是F(−1,1)和曲线切线(1,1−x2−x)的夹角,不是方向角)=∣F∣cosαds=2⋅1⋅2−x+1−x2ds=2⋅1⋅2−x+1−x21+y′2dx
以上的计算还是比较复杂一点的,是直接计算,没有对F进行两次正交分解。
考虑
F
→
\overrightarrow{\bold F}
F的
x
x
x分量做功
d
W
x
=
∫
P
(
x
,
y
)
i
d
r
=
∫
P
(
x
,
y
)
∣
d
r
→
∣
cos
α
(
α
是
x
轴方向角
)
=
∫
1
−
x
2
d
s
=
∫
1
−
x
2
⋅
1
1
−
x
2
d
x
=
1
\begin{aligned} dW_x&=\int P(x,y)\bold id\bold r\\ &=\int P(x,y)|d\overrightarrow{\bold r} |\cos\alpha(\alpha是x轴方向角)\\ &=\int \sqrt{1-x^2}ds\\ &=\int \sqrt{1-x^2}\cdot\frac{1}{\sqrt{1-x^2}}dx=1 \end{aligned}
dWx=∫P(x,y)idr=∫P(x,y)∣dr∣cosα(α是x轴方向角)=∫1−x2ds=∫1−x2⋅1−x21dx=1
格林公式(非常重要)
设闭区域
D
D
D由分段光滑曲线
L
L
L围成,若函数
P
(
x
,
y
)
P(x,y)
P(x,y)及
Q
(
x
,
y
)
Q(x,y)
Q(x,y)在
D
D
D上有连续一阶偏导数,则有
∬
D
(
∂
Q
∂
x
−
∂
P
∂
y
)
d
x
d
y
=
∮
L
P
d
x
+
Q
d
y
\iint\limits_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy=\oint_LPdx+Qdy
D∬(∂x∂Q−∂y∂P)dxdy=∮LPdx+Qdy
其中
L
L
L是区域
D
D
D边界上取正向的曲线。
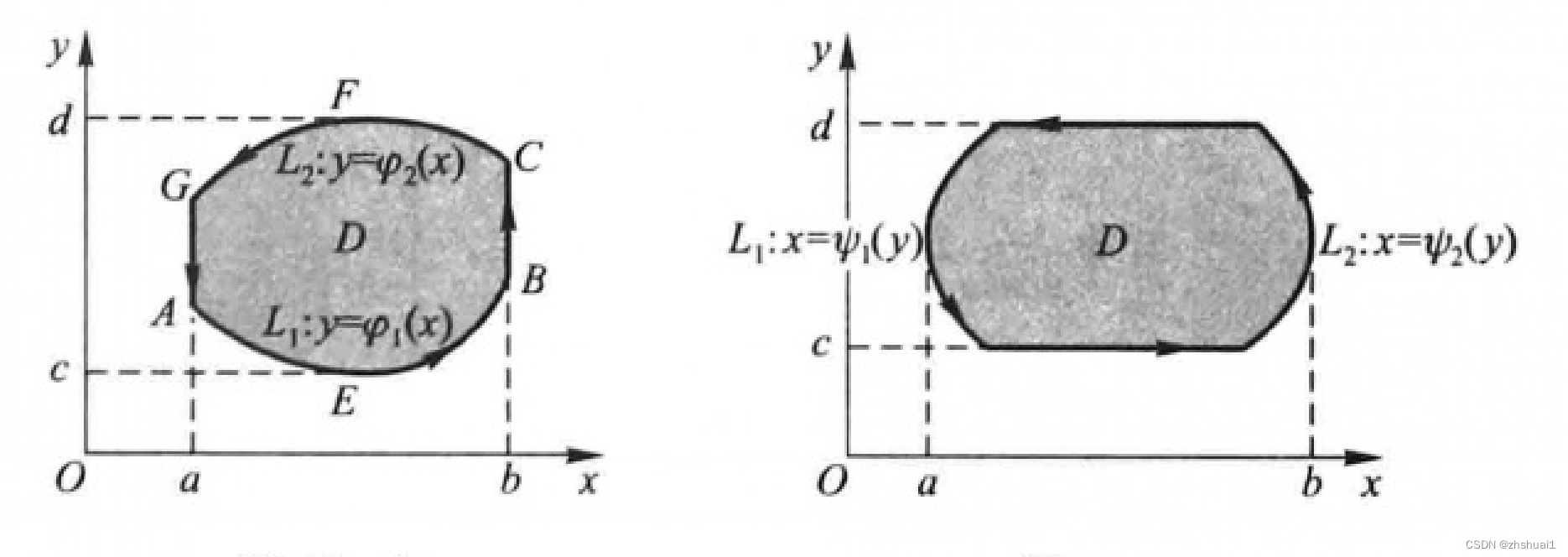
证明:首先假设区域
D
D
D既是X型,又是Y型的,则
∬
D
∂
P
∂
y
d
x
d
y
=
∫
a
b
∫
φ
1
(
x
)
φ
2
(
x
)
∂
P
∂
y
d
y
d
x
=
∫
a
b
(
P
(
x
,
φ
2
(
x
)
)
−
P
(
x
,
φ
1
(
x
)
)
)
d
x
\begin{aligned} &\iint\limits_D\frac{\partial P}{\partial y}dxdy\\ =&\int_a^b\int_{\varphi_1(x)}^{\varphi_2(x)}\frac{\partial P}{\partial y}dydx\\ =&\int_a^b\left (P(x,\varphi_2(x))-P(x,\varphi_1(x))\right)dx \end{aligned}
==D∬∂y∂Pdxdy∫ab∫φ1(x)φ2(x)∂y∂Pdydx∫ab(P(x,φ2(x))−P(x,φ1(x)))dx
另一方面
∮
L
P
d
x
=
∫
B
C
P
d
x
+
∫
C
F
G
P
d
x
+
∫
G
A
P
d
x
+
∫
A
E
B
P
d
x
=
0
+
∫
b
a
P
(
x
,
φ
2
(
x
)
)
d
x
+
0
+
∫
a
b
P
(
x
,
φ
1
(
x
)
)
d
x
=
∫
a
b
(
−
P
(
x
,
φ
2
(
x
)
)
+
P
(
x
,
φ
1
(
x
)
)
)
d
x
=
−
∬
D
∂
P
∂
y
d
x
d
y
\begin{aligned} &\oint_LPdx\\ =&\int_{BC}Pdx+\int_{CFG}Pdx+\int_{GA}Pdx+\int_{AEB}Pdx\\ =&0+\int_b^aP(x,\varphi_2(x))dx+0+\int_a^bP(x,\varphi_1(x))dx\\ =&\int_a^b\left (-P(x,\varphi_2(x))+P(x,\varphi_1(x))\right)dx\\ =&-\iint\limits_D\frac{\partial P}{\partial y}dxdy \end{aligned}
====∮LPdx∫BCPdx+∫CFGPdx+∫GAPdx+∫AEBPdx0+∫baP(x,φ2(x))dx+0+∫abP(x,φ1(x))dx∫ab(−P(x,φ2(x))+P(x,φ1(x)))dx−D∬∂y∂Pdxdy
同理,因为区域
D
D
D也是Y型的,可得
∮
L
Q
d
y
=
∬
D
∂
Q
∂
x
d
x
d
y
\oint_L Qdy = \iint\limits_D\frac{\partial Q}{\partial x}dxdy
∮LQdy=D∬∂x∂Qdxdy
若区域不是X型或者Y型,则可以通过将其切割的方式,得到若干既是X型,又是Y型的区域。在切割线上,二重积分为0,曲线积分方向相反恰好相互抵消。
格林公式还是很神奇的,意思是,一个闭区域的二重积分可以只通过边界就确定,和内部情况无关。乍一看很难理解,怎么可能呢?但是仔细一想,二重积分的被积函数是 Q Q Q的偏导数。可以这么理解,偏导数在一个闭区域里无论怎样变化,你多了一重积分,都不重要了,只和闭区域边界上变化量有关,而这个变化量是可以通过边界上看到的。也就是二重积分关心的是细节,但是累积之后其实只和进入和流出边界的变化量有关,边界值是一个最终结果,可以确定变化量。实际格林公式的证明过程也是这么个道理。高斯公式类似。
曲线积分和路径无关的条件
设区域
G
G
G是一个单连通区域,若函数
P
(
x
,
y
)
P(x,y)
P(x,y)和
Q
(
x
,
y
)
Q(x,y)
Q(x,y)在
G
G
G内具有一阶连续偏导数,则曲线积分
∫
=
P
d
x
+
Q
d
y
\int=Pdx+Qdy
∫=Pdx+Qdy在
G
G
G内与路径无关的充要条件是
∂
Q
∂
x
=
∂
P
∂
y
\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}
∂x∂Q=∂y∂P在
G
G
G内恒成立。
曲面积分
第一类曲面积分
定义:设曲面
Σ
\Sigma
Σ是光滑的,函数
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)在
Σ
\Sigma
Σ上有界. 把
Σ
\Sigma
Σ任意分成
n
n
n个小块
Δ
S
i
\Delta S_i
ΔSi(
Δ
S
i
\Delta S_i
ΔSi同时也表示第
i
i
i个小块的面积),设
f
(
ξ
i
,
η
i
,
ζ
i
)
Δ
S
i
(
i
=
1
,
2
,
3...
n
)
f(\xi_i,\eta_i,\zeta_i)\Delta S_i(i=1,2,3...n)
f(ξi,ηi,ζi)ΔSi(i=1,2,3...n),并作和
∑
i
=
1
n
f
(
ξ
i
,
η
i
,
ζ
i
)
Δ
S
i
\sum\limits_{i=1}^{n}f(\xi_i,\eta_i,\zeta_i)\Delta S_i
i=1∑nf(ξi,ηi,ζi)ΔSi,如果当各个小块曲面的直径最大值
λ
→
0
\lambda\to0
λ→0时,这个和的极限总存在,且与曲面
Σ
\Sigma
Σ的分法及点
(
ξ
i
,
η
i
,
ζ
i
)
(\xi_i,\eta_i,\zeta_i)
(ξi,ηi,ζi)的取法无关,那么称此极限为函数
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)在曲面
Σ
\Sigma
Σ上对面积的曲面积分或者第一类曲面积分,记作
∬
Σ
f
(
x
,
y
,
z
)
d
S
\iint\limits_\Sigma f(x,y,z)dS
Σ∬f(x,y,z)dS,即
∬
Σ
f
(
x
,
y
,
z
)
d
S
=
lim
λ
→
0
∑
i
=
1
n
f
(
ξ
i
,
η
i
,
ζ
i
)
Δ
S
i
\iint\limits_\Sigma f(x,y,z)dS=\lim_{\lambda\to0}\sum\limits_{i=1}^{n}f(\xi_i,\eta_i,\zeta_i)\Delta S_i
Σ∬f(x,y,z)dS=λ→0limi=1∑nf(ξi,ηi,ζi)ΔSi
其中,
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)叫做被积函数,
Σ
\Sigma
Σ叫做积分曲面。
第一类曲面积分计算方法
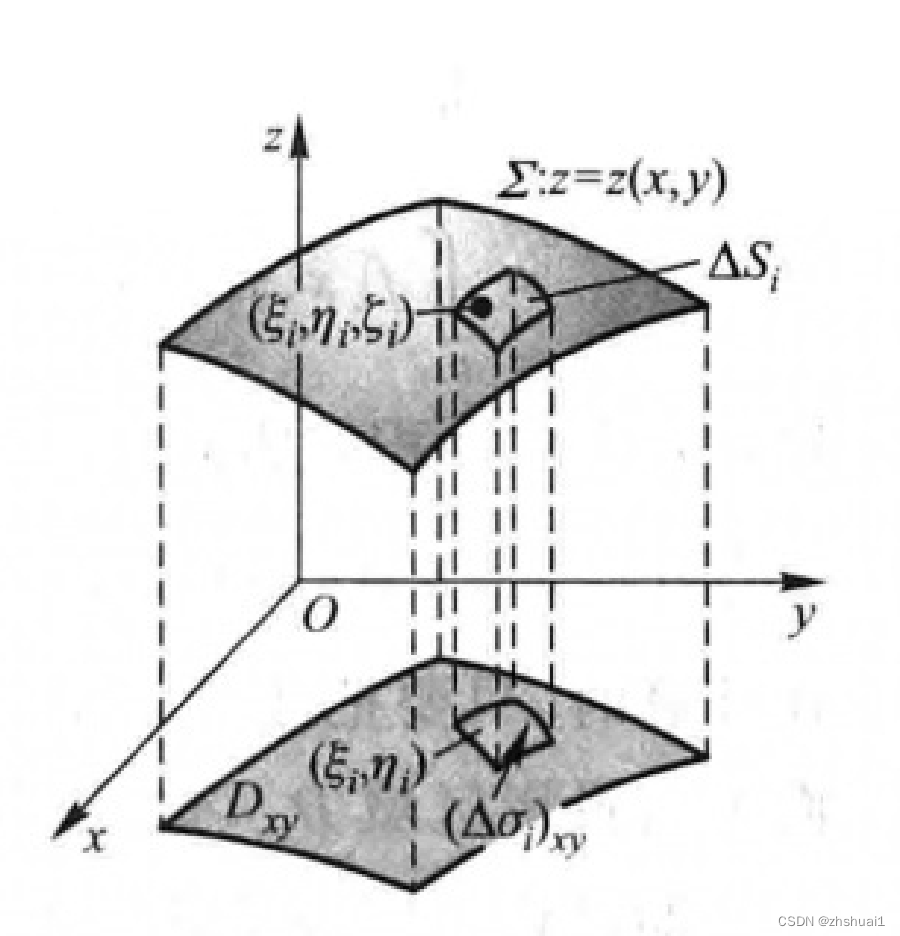
∬
Σ
f
(
x
,
y
,
z
)
d
S
=
∬
D
x
y
f
(
x
,
y
,
z
)
z
x
2
+
z
y
2
+
1
d
x
d
y
\iint\limits_\Sigma f(x,y,z)dS=\iint\limits_{D_{xy}} f(x,y,z)\sqrt{z_x^2+z_y^2+1}dxdy
Σ∬f(x,y,z)dS=Dxy∬f(x,y,z)zx2+zy2+1dxdy
严格证明可能需要使用积分中值定理。这里只做一个说明:
Δ
S
i
⋅
cos
γ
=
Δ
σ
i
\Delta S_i\cdot\cos\gamma=\Delta\sigma_i
ΔSi⋅cosγ=Δσi,
γ
\gamma
γ是
z
z
z轴方向角,有
cos
γ
=
k
⋅
n
∣
k
∣
∣
n
∣
=
−
1
z
x
2
+
z
y
2
+
1
\cos\gamma=\frac{\bold k\cdot\bold n}{|\bold k||\bold n|}=\frac{-1}{\sqrt{z_x^2+z_y^2+1}}
cosγ=∣k∣∣n∣k⋅n=zx2+zy2+1−1
∬
Σ
f
(
x
,
y
,
z
)
d
S
=
∬
D
x
y
f
(
x
,
y
,
z
)
1
cos
γ
d
x
d
y
=
∬
D
x
y
f
(
x
,
y
,
z
)
z
x
2
+
z
y
2
+
1
d
x
d
y
\iint\limits_\Sigma f(x,y,z)dS\\ =\iint\limits_{D_{xy}} f(x,y,z)\frac{1}{\cos\gamma}dxdy\\ =\iint\limits_{D_{xy}} f(x,y,z)\sqrt{z_x^2+z_y^2+1}dxdy
Σ∬f(x,y,z)dS=Dxy∬f(x,y,z)cosγ1dxdy=Dxy∬f(x,y,z)zx2+zy2+1dxdy
第二类曲面积分
高斯公式
定理 设空间闭区域
Ω
\Omega
Ω是有分段光滑的闭曲面
Σ
\Sigma
Σ围成,若函数
P
(
x
,
y
,
z
)
,
Q
(
x
,
y
,
z
)
,
R
(
x
,
y
,
z
)
P(x,y,z), Q(x,y,z),R(x,y,z)
P(x,y,z),Q(x,y,z),R(x,y,z)在
Ω
\Omega
Ω上具有连续的一阶偏导数,则有
∭
Ω
∂
P
∂
x
+
∂
Q
∂
y
+
∂
R
∂
z
=
∯
Σ
P
d
y
d
z
+
Q
d
x
d
z
+
R
d
x
d
y
\iiint\limits_{\Omega}\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=\oiint\limits_\Sigma Pdydz+Qdxdz+Rdxdy
Ω∭∂x∂P+∂y∂Q+∂z∂R=Σ∬Pdydz+Qdxdz+Rdxdy或
∭
Ω
∂
P
∂
x
+
∂
Q
∂
y
+
∂
R
∂
z
=
∯
Σ
P
cos
α
+
Q
cos
β
+
R
cos
γ
d
S
\iiint\limits_{\Omega}\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=\oiint\limits_\Sigma P\cos\alpha+Q\cos\beta+R\cos\gamma dS
Ω∭∂x∂P+∂y∂Q+∂z∂R=Σ∬Pcosα+Qcosβ+RcosγdS
这里,
Σ
\Sigma
Σ是
Ω
\Omega
Ω整个边界曲面的外侧,
cos
α
,
cos
β
,
cos
γ
\cos\alpha,\cos\beta,\cos\gamma
cosα,cosβ,cosγ是
Σ
\Sigma
Σ在点
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)处的法向量方向余弦。
沿任意闭曲面积分为0的条件
斯托克斯公式
定理1 设
Γ
\Gamma
Γ为分段光滑的空间有向闭曲线,
Σ
\Sigma
Σ是以
Γ
\Gamma
Γ为边界的分片光滑的有向曲面,
Γ
\Gamma
Γ的正向与
Σ
\Sigma
Σ的侧符合右手规则,若函数
P
(
x
,
y
,
z
)
,
Q
(
x
,
y
,
z
)
,
R
(
x
,
y
,
z
)
P(x,y,z),Q(x,y,z),R(x,y,z)
P(x,y,z),Q(x,y,z),R(x,y,z)在曲面
Σ
\Sigma
Σ(连通边界
Γ
\Gamma
Γ)上具有一阶连续偏导数,则有
∬
Σ
(
∂
R
∂
y
−
∂
Q
∂
z
)
d
y
d
z
−
(
∂
R
∂
x
−
∂
P
∂
z
)
d
y
d
z
+
(
∂
Q
∂
x
−
∂
P
∂
y
)
d
y
d
z
=
∮
Γ
P
d
x
+
Q
d
y
+
R
d
z
\iint\limits_\Sigma(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})dydz -(\frac{\partial R}{\partial x}-\frac{\partial P}{\partial z})dydz +(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dydz\\ =\oint_\Gamma Pdx+Qdy+Rdz
Σ∬(∂y∂R−∂z∂Q)dydz−(∂x∂R−∂z∂P)dydz+(∂x∂Q−∂y∂P)dydz=∮ΓPdx+Qdy+Rdz
表述成行列式形式
∬
Σ
∣
d
y
d
z
d
z
d
x
d
x
d
y
∂
∂
x
∂
∂
y
∂
∂
z
P
Q
R
∣
=
∮
Γ
P
d
x
+
Q
d
y
+
R
d
z
\iint\limits_\Sigma\left| \begin{aligned} dydz &\ \ \ \ \ \ dzdx & dxdy \\ \frac{\partial}{\partial x} &\ \ \ \ \ \ \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P &\ \ \ \ \ \ Q &R \\ \end{aligned} \right|=\oint_\Gamma Pdx+Qdy+Rdz
Σ∬
dydz∂x∂P dzdx ∂y∂ Qdxdy∂z∂R
=∮ΓPdx+Qdy+Rdz
课本上给了一种证明,本身可以做点简化,另外就是只是通过公式化的推导,并没有对斯托克斯公式本身的含义做很好的解释,这里做些改进。
证明:先假设
Σ
\Sigma
Σ与平行于
z
z
z轴的直线相交不多于一点,并设
Σ
\Sigma
Σ为曲面
z
=
f
(
x
,
y
)
z=f(x,y)
z=f(x,y)的上侧,
Σ
\Sigma
Σ的正向边界曲线
Γ
\Gamma
Γ在
x
O
y
xOy
xOy面上的投影为平面有向曲线
C
C
C,
C
C
C锁围成的闭区域为
D
x
y
D_{xy}
Dxy
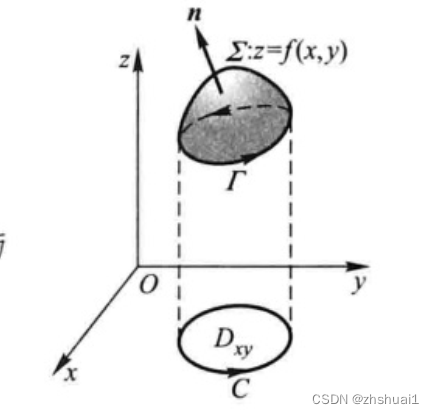
我们设法把曲面积分
∬
Σ
∂
P
∂
z
d
z
d
x
−
∂
P
∂
y
d
x
d
y
\iint\limits_\Sigma \frac{\partial P}{\partial z}dzdx-\frac{\partial P}{\partial y}dxdy
Σ∬∂z∂Pdzdx−∂y∂Pdxdy化为闭区域
D
x
y
D_{xy}
Dxy上的二重积分,然后通过格林公式使它与曲线积分相联系。
∬
Σ
∂
P
∂
z
d
z
d
x
−
∂
P
∂
y
d
x
d
y
=
∬
Σ
∂
P
∂
z
d
z
d
y
d
y
d
x
−
∂
P
∂
y
d
x
d
y
=
∬
Σ
∂
P
∂
z
z
y
d
x
d
y
−
∂
P
∂
y
d
x
d
y
\iint\limits_\Sigma \frac{\partial P}{\partial z}dzdx-\frac{\partial P}{\partial y}dxdy \\ =\iint\limits_\Sigma \frac{\partial P}{\partial z}\frac{dz}{dy}dydx-\frac{\partial P}{\partial y}dxdy\\ =\iint\limits_\Sigma \frac{\partial P}{\partial z}z_ydxdy-\frac{\partial P}{\partial y}dxdy
Σ∬∂z∂Pdzdx−∂y∂Pdxdy=Σ∬∂z∂Pdydzdydx−∂y∂Pdxdy=Σ∬∂z∂Pzydxdy−∂y∂Pdxdy
另外的方法:
我们把曲面
Σ
\Sigma
Σ使用平面组
x
=
a
i
,
y
=
b
i
x=a_i,y=b_i
x=ai,y=bi切割成一块一块,对于其中的一块由平面
x
=
a
1
,
x
=
a
2
,
y
=
b
1
,
y
=
b
2
x=a_1, x=a_2, y=b_1,y=b_2
x=a1,x=a2,y=b1,y=b2和曲面的交点为
A
(
a
1
,
b
1
,
z
A
)
,
B
(
a
2
,
b
1
,
z
B
)
,
C
(
a
2
,
b
2
,
z
C
)
,
D
(
a
1
,
b
2
,
z
D
)
A(a_1,b_1,z_A),B(a_2,b_1,z_B),C(a_2,b_2,z_C),D(a_1,b_2,z_D)
A(a1,b1,zA),B(a2,b1,zB),C(a2,b2,zC),D(a1,b2,zD),来求曲线积分
∮
Γ
R
d
z
=
∫
A
B
+
∫
B
C
+
∫
C
D
+
∫
D
A
R
d
z
\oint_\Gamma Rdz=\int_{AB}+\int_{BC}+\int_{CD}+\int_{DA} Rdz
∮ΓRdz=∫AB+∫BC+∫CD+∫DARdz
由格林公式
∬
D
y
z
∂
R
∂
y
d
y
d
z
=
∫
A
B
+
∫
C
D
R
d
z
−
∬
D
y
z
∂
R
∂
x
d
x
d
z
=
∫
B
C
+
∫
D
A
R
d
z
\iint\limits_{D_{yz}}\frac{\partial R}{\partial y}dydz =\int_{AB}+\int_{CD} Rdz\\ -\iint\limits_{D_{yz}}\frac{\partial R}{\partial x}dxdz =\int_{BC}+\int_{DA} Rdz
Dyz∬∂y∂Rdydz=∫AB+∫CDRdz−Dyz∬∂x∂Rdxdz=∫BC+∫DARdz
也就是说,
R
R
R沿曲线
Γ
\Gamma
Γ的线积分,可以拆成两部分,一部分是是x轴方向的积分,另一部分是y轴方向的积分。
梯度、散度、旋度在向量分析中会有更详细的研究和笔记。