题目如下：

在火影忍者的世界里，令敌人捉摸不透是非常关键的。

我们的主角漩涡鸣人所拥有的一个招数——多重影分身之术——就是一个很好的例子。

影分身是由鸣人身体的查克拉能量制造的，使用的查克拉越多，制造出的影分身越强。

针对不同的作战情况，鸣人可以选择制造出各种强度的影分身，有的用来佯攻，有的用来发起致命一击。

那么问题来了，假设鸣人的查克拉能量为 $M$，他影分身的个数最多为 $N$，那么制造影分身时有多少种不同的分配方法？

注意：

影分身可以分配0点能量。
分配方案不考虑顺序，例如：$M=7,N=3$，那么 $(2,2,3)$ 和 $(2,3,2)$ 被视为同一种方案。

输入格式

第一行是测试数据的数目 $t$。

以下每行均包含二个整数 $M$ 和 $N$，以空格分开。

输出格式

对输入的每组数据 $M$ 和 $N$，用一行输出分配的方法数。

数据范围

$0\le t\le 20$,
$1\le M,N\le 10$

输入样例：

1
7 3

输出样例：

8

难度：中等
时/空限制：1s / 64MB

题解 or 思路：

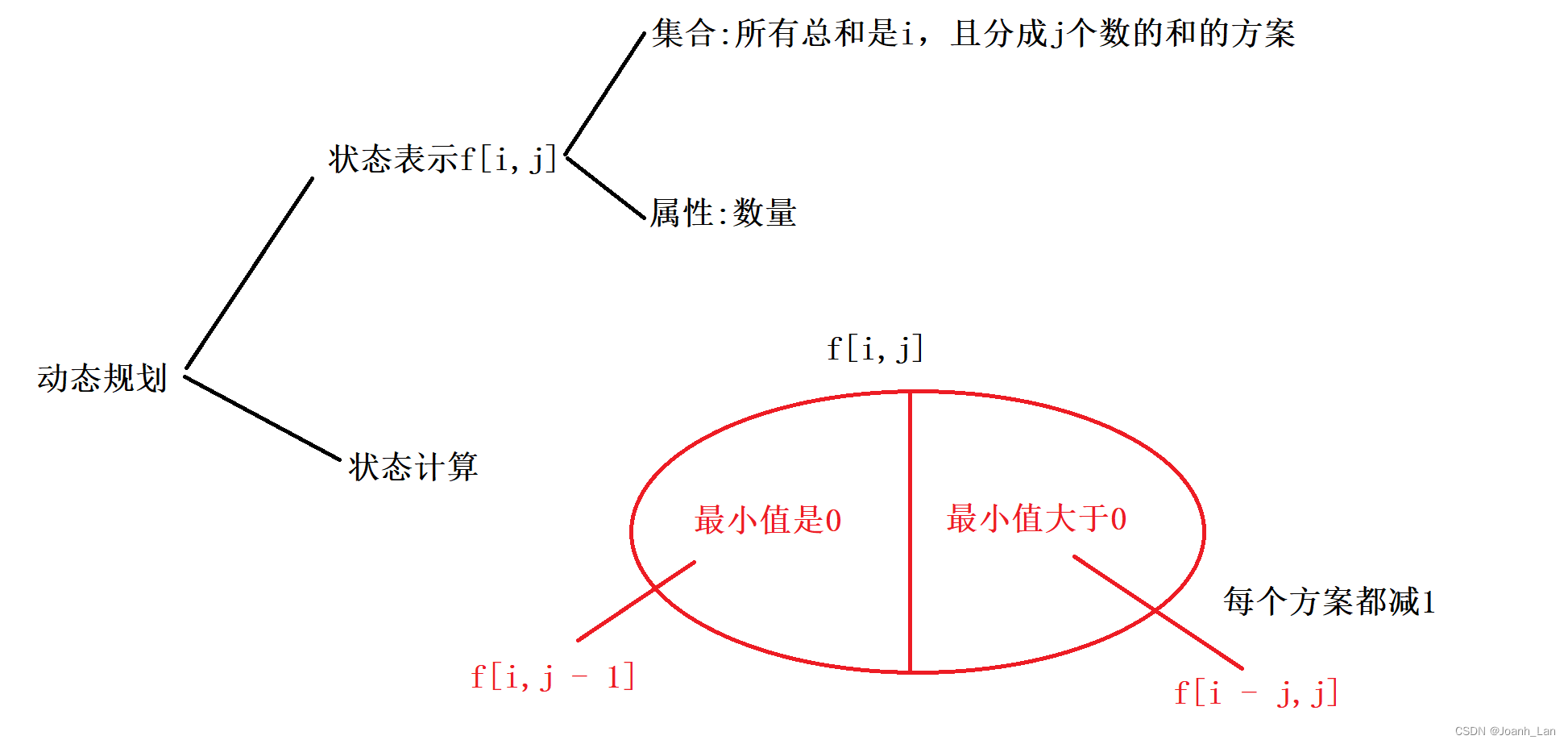
状态定义：

$dp[i][j]$ 长度为 $j$， 和为 $i$ 的方案数

状态转移：

因为和位置没有关系我们可以这样考虑
*** … *** x
我们考虑 x 的取值

• $x=0$
  $dp[i][j]+=dp[i][j-1]$
  这个非常好理解
• $x!=0andi-j\ge 0$
  $dp[i][j]+=dp[i-j][j]$
  这个我们如何去理解：
  相当于做了映射，把所有元素 - 1， 其实还是一一对应关系
  

初始化：

dp[0][0] = 1

这个也是整数划分的一个模型

AC 代码如下：

int dp[15][15];
void solve()
{
    dp[0][0] = 1;
    for (int i = 0; i <= 10; i++)
        for (int j = 1; j <= 10; j++)
        {
            dp[i][j] += dp[i][j - 1];
            if (i - j >= 0)
                dp[i][j] += dp[i - j][j];
        }
}
int main()
{
    solve();
    int _;
    cin >> _;
    while (_--)
    {
        int n, m;
        cin >> m >> n;
        cout << dp[m][n] << '\n';
    }
}