这一篇文章叫做 数据驱动的坐标发现与方程发现算法。
想回答的问题很简单,“如何根据数据写方程”。
想想牛顿的处境,如何根据各种不同物体下落的数据,写出万有引力的数学公式的。这篇文章就是来做这件事的。当然,这篇论文并没有从牛顿视角,完全去思考牛顿所想。而是利用现有的深度学习技术 和 动力学重构的方法 。提出了一种框架,基于现有的计算机技术,去发现物质运动背后的物理规律。
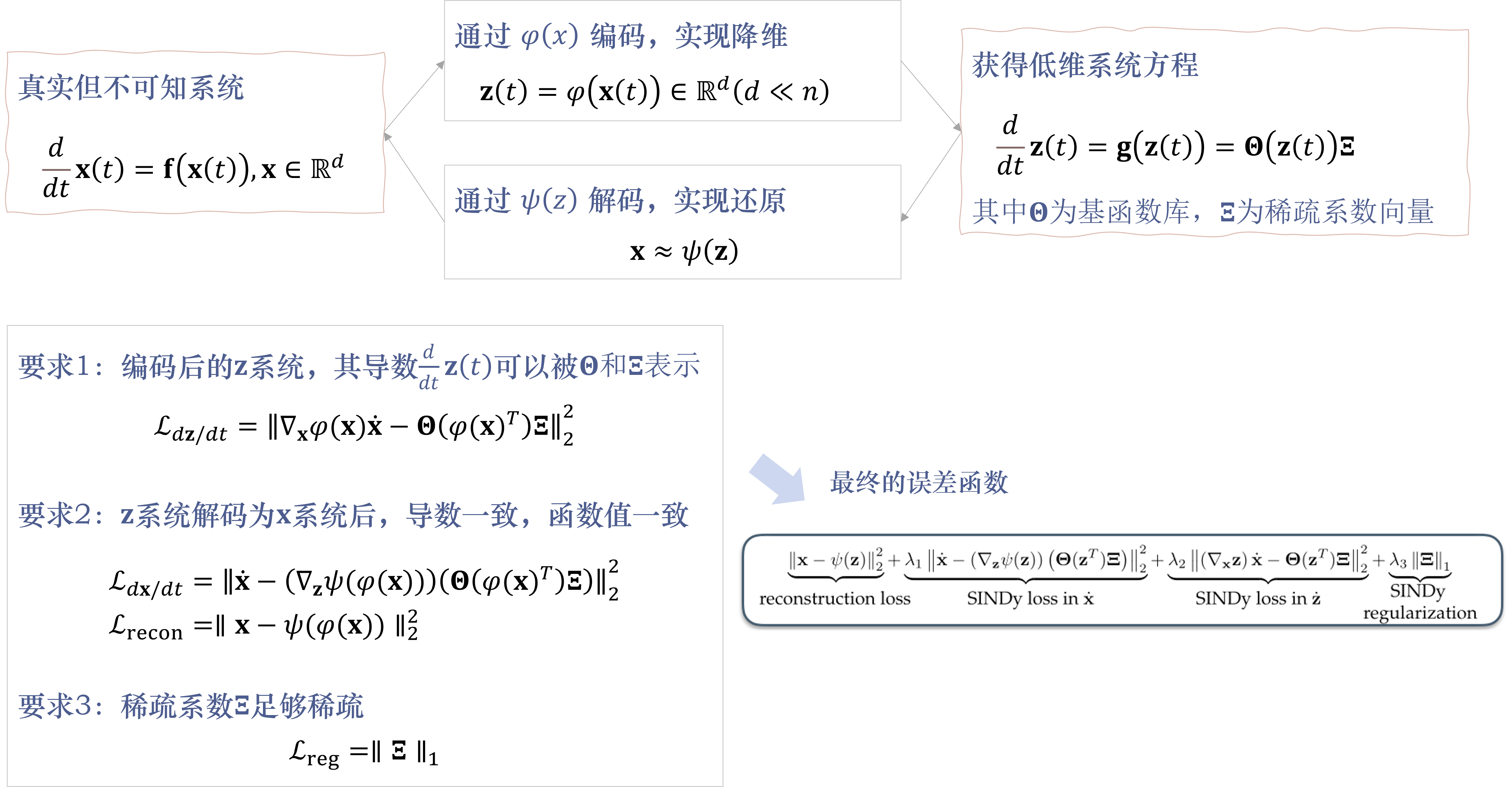
这里直接给出这篇方法的核心思路图,我们后面会逐个讲解。
正文
Data-driven discovery of coordinates and governing equations
作者包括华盛顿大学的 Kathleen Champion 和 Steven L. Brunton。Brunton的SINDy方法,我们在 基于RNN进行动力学重构 的文章中也提到过。
这篇文章的主要创新点在于
- 在数据降维这块,提出可以用神经网络的算法来进行数据编码,从而来实现降维。
这在文中被称为自编码器,学习一个用于表示数据的坐标系,希望经过坐标系的变换,能够提取出更加明显和有效的动力学特征。 - 结合了非线性动力学识别(SINDy)的方法,来进行参数的拟合。这在下文中也会介绍。
核心方法
首先,我们考虑一个 n n n 维状态的动力学系统如公式(1)所示,其中 x ( t ) ∈ R n \mathbf{x}(t) \in \mathbb{R}^n x(t)∈Rn 。
d d t x ( t ) = f ( x ( t ) ) (1) \frac{d}{d t} \mathbf{x}(t)=\mathbf{f}(\mathbf{x}(t)) \tag{1} dtdx(t)=f(x(t))(1)
我们的目标是
- 寻求一组具有相关动态模型的约化坐标。即 z ( t ) = φ ( x ( t ) ) ∈ R d ( d ≪ n ) \mathbf{z}(t)=\varphi(\mathbf{x}(t)) \in \mathbb{R}^d(d \ll n) z(t)=φ(x(t))∈Rd(d≪n),这个新坐标下的一个动力学维数远远小于原始系统。
- 能够给出在这个简约坐标下对应的动力学方程
d d t z ( t ) = g ( z ( t ) ) (2) \frac{d}{d t} \mathbf{z}(t)=\mathbf{g}(\mathbf{z}(t)) \tag{2} dtdz(t)=g(z(t))(2) - 这个方法同时还提出对应的编码函数 z = φ ( x ) \mathbf{z}=\varphi(\mathbf{x}) z=φ(x) 和 解码函数 x ≈ ψ ( z ) \mathbf{x} \approx \psi(\mathbf{z}) x≈ψ(z)。实现在简化坐标和还原原始坐标之间的转化。
我们希望在对原数据进行
z
=
φ
(
x
)
\mathbf{z}=\varphi(\mathbf{x})
z=φ(x) 的编码之后,能更方便我们使用公式(3)的形式来进行描述。其中,
基函数库
Θ
(
z
)
=
[
θ
1
(
z
)
,
θ
2
(
z
)
,
…
,
θ
p
(
z
)
]
\Theta(\mathbf{z})=\left[\boldsymbol{\theta}_1(\mathbf{z}), \boldsymbol{\theta}_2(\mathbf{z}), \ldots, \boldsymbol{\theta}_p(\mathbf{z})\right]
Θ(z)=[θ1(z),θ2(z),…,θp(z)] 是由多项式或初等函数所组成。
稀疏系数向量
Ξ
=
[
ξ
1
,
…
,
ξ
d
]
\boldsymbol{\Xi}=\left[\boldsymbol{\xi}_1, \ldots, \boldsymbol{\xi}_d\right]
Ξ=[ξ1,…,ξd] 指的是其中的非零系数尽可能少,大部分
ξ
i
=
0
\boldsymbol{\xi}_i=0
ξi=0.
d d t z ( t ) = g ( z ( t ) ) = Θ ( z ( t ) ) Ξ (3) \frac{d}{d t} \mathbf{z}(t)=\mathbf{g}(\mathbf{z}(t))=\boldsymbol{\Theta}(\mathbf{z}(t)) \boldsymbol{\Xi} \tag{3} dtdz(t)=g(z(t))=Θ(z(t))Ξ(3)
(误差函数与编码器) 上式基函数库
Θ
\Theta
Θ 是在训练之前由人类专家指定好的,而稀疏系数向量是在训练的过程中随之确定的。由于我们要求公式(3)是尽量成立的,再令
z
˙
(
t
)
=
∇
x
φ
(
x
(
t
)
)
x
˙
(
t
)
\dot{\mathbf{z}}(t)=\nabla_{\mathbf{x}} \varphi(\mathbf{x}(t)) \dot{\mathbf{x}}(t)
z˙(t)=∇xφ(x(t))x˙(t) ,可以得出我们误差函数 其实只是把公式(3)移项,让等式左右相减,尽量为0
L
d
z
/
d
t
=
∥
∇
x
φ
(
x
)
x
˙
−
Θ
(
φ
(
x
)
T
)
Ξ
∥
2
2
(4)
\mathcal{L}_{d \mathbf{z} / d t}=\left\|\nabla_{\mathbf{x}} \varphi(\mathbf{x}) \dot{\mathbf{x}}-\boldsymbol{\Theta}\left(\varphi(\mathbf{x})^T\right) \boldsymbol{\Xi}\right\|_2^2 \tag{4}
Ldz/dt=
∇xφ(x)x˙−Θ(φ(x)T)Ξ
22(4)
(误差函数与解码器) 但公式(4)只与编码器
φ
\varphi
φ 有关,我们还希望得到正确解码器
ψ
\psi
ψ,要求解码后能够还原
x
˙
\mathbf{\dot{x}}
x˙ 和
x
\mathbf{x}
x 的时间序列。于是可以写出下面两个误差函数
L
d
x
/
d
t
=
∥
x
˙
−
(
∇
z
ψ
(
φ
(
x
)
)
)
(
Θ
(
φ
(
x
)
T
)
Ξ
)
∥
2
2
.
L
recon
=
∥
x
−
ψ
(
φ
(
x
)
)
∥
2
2
,
(5,6)
\begin{aligned} \mathcal{L}_{d \mathbf{x} / d t}&=\left\|\dot{\mathbf{x}}-\left(\nabla_{\mathbf{z}} \psi(\varphi(\mathbf{x}))\right)\left(\boldsymbol{\Theta}\left(\varphi(\mathbf{x})^T\right) \boldsymbol{\Xi}\right)\right\|_2^2 . \\ \mathcal{L}_{\text {recon }}&=\|\mathbf{x}-\psi(\varphi(\mathbf{x}))\|_2^2, \end{aligned} \tag{5,6}
Ldx/dtLrecon =
x˙−(∇zψ(φ(x)))(Θ(φ(x)T)Ξ)
22.=∥x−ψ(φ(x))∥22,(5,6)
(误差函数与稀疏系数) 此外,我们还希望用于描述编码后系统,所使用的函数越少越好。于是我们对使用L1范数来进行约束。即 L reg = ∣ ∣ Ξ ∣ ∣ 1 \mathcal{L}_{\text {reg}}= ||\boldsymbol{\Xi}||_1 Lreg=∣∣Ξ∣∣1
备注: ∥ x ∥ 0 \|x\|_0 ∥x∥0 表示非零元素的个数,是NP难题,一般用L1范数代替。
L1范数, ∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \|x\|_1=\sum_{i=1}^n\left|x_i\right| ∥x∥1=∑i=1n∣xi∣,一般用来进行稀疏优化。
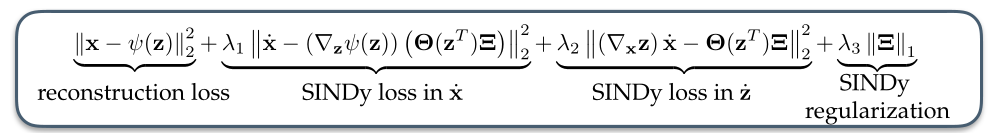
(最终的误差函数) 现在,我们把上面误差函数汇总,得到了本文最终所使用的误差函数-公式(7),其中
λ
1
,
λ
2
,
λ
3
\lambda_1, \lambda_2, \lambda_3
λ1,λ2,λ3 是超参数。
L recon + λ 1 L d x / d t + λ 2 L d z / d t + λ 3 L r e g (7) \mathcal{L}_{\text {recon }}+\lambda_1 \mathcal{L}_{d \mathbf{x} / d t}+\lambda_2 \mathcal{L}_{d \mathbf{z} / d t}+\lambda_3 \mathcal{L}_{\mathrm{reg}} \tag{7} Lrecon +λ1Ldx/dt+λ2Ldz/dt+λ3Lreg(7)
除了使用 L 1 L_1 L1 正则化之外,作者还提出可以使用SINDy的顺序阈值方法来纳入训练过程。就是在训练的期间,固定的时间间隔内,低于某个阈值的系数会被强行固定为0,然后使用模型中剩余的项继续训练。
结果 Result
以Lorenz系统为例,原始系统为
z
˙
1
=
σ
(
z
2
−
z
1
)
z
˙
2
=
z
1
(
ρ
−
z
3
)
−
z
2
z
˙
3
=
z
1
z
2
−
β
z
3
\begin{aligned} & \dot{z}_1=\sigma\left(z_2-z_1\right) \\ & \dot{z}_2=z_1\left(\rho-z_3\right)-z_2 \\ & \dot{z}_3=z_1 z_2-\beta z_3 \end{aligned}
z˙1=σ(z2−z1)z˙2=z1(ρ−z3)−z2z˙3=z1z2−βz3
假设我们采集的数据是由这三个状态变量的非线性组合形成的时间序列数据
x
(
t
)
=
u
1
z
1
(
t
)
+
u
2
z
2
(
t
)
+
u
3
z
3
(
t
)
+
u
4
z
1
(
t
)
3
+
u
5
z
2
(
t
)
3
+
u
6
z
3
(
t
)
3
.
\mathbf{x}(t)=\mathbf{u}_1 z_1(t)+\mathbf{u}_2 z_2(t)+\mathbf{u}_3 z_3(t)+\mathbf{u}_4 z_1(t)^3+\mathbf{u}_5 z_2(t)^3+\mathbf{u}_6 z_3(t)^3 .
x(t)=u1z1(t)+u2z2(t)+u3z3(t)+u4z1(t)3+u5z2(t)3+u6z3(t)3.
我们看着这个组合的数据,去重构动力学方程。得到结果如下
z
˙
1
=
−
10.0
z
1
+
10.0
z
2
z
˙
2
=
27.7
z
1
−
0.9
z
2
−
5.5
z
1
z
3
z
˙
3
=
−
2.7
z
3
+
5.5
z
1
z
2
\begin{aligned} & \dot{z}_1=-10.0 z_1+10.0 z_2 \\ & \dot{z}_2=27.7 z_1-0.9 z_2-5.5 z_1 z_3 \\ & \dot{z}_3=-2.7 z_3+5.5 z_1 z_2 \end{aligned}
z˙1=−10.0z1+10.0z2z˙2=27.7z1−0.9z2−5.5z1z3z˙3=−2.7z3+5.5z1z2
可以验证还原出的系统与真实系统是基本等价的。

总结
回顾这篇文章开头的流程图,是否有加深理解呢?

相关链接
- SINDy源码
- 本文的论文原文
- Matlab - 非线性动力学/混沌系统/复杂性科学/系统科学常用工具
- Matlab - RK4的Lorenz仿真
- 论文泛读 - 基于RNN建模: Reconstructing computational system dynamics from neural data with recurrent neural


![[leetcode] 63. 不同路径 II](https://img-blog.csdnimg.cn/direct/a36c1b59f2eb48eebd27dc7ba26116ca.png)


![[方法] Unity 实现仿《原神》第三人称跟随相机 v1.1](https://img-blog.csdnimg.cn/direct/26d149d2c5bf47a081a5fa7cc458b7b4.png)