牛客

一、DP30买卖股票的最好时机（一）

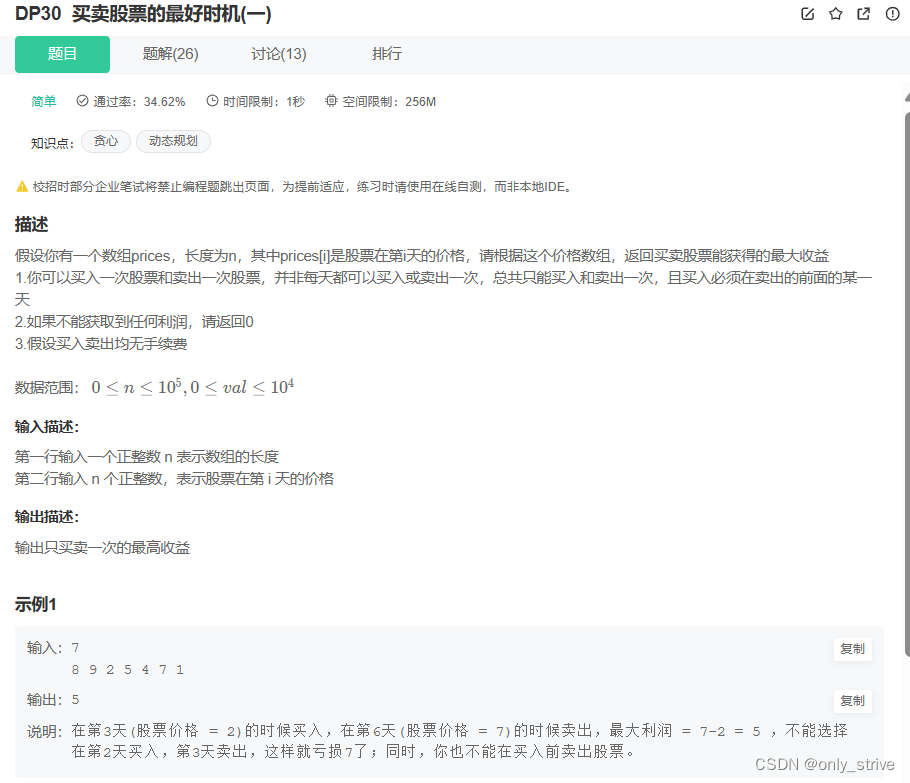
算法：虽然题目标了DP但是用贪心更快页更容易理解

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        // while (in.hasNextInt()) { // 注意 while 处理多个 case
        //     int a = in.nextInt();
        //     int b = in.nextInt();
        //     System.out.println(a + b);
        // }

        //贪心，维护一个当前最小值（买入）
        int len = in.nextInt();
        int preMin = in.nextInt();
        int max = 0;
        for(int i = 1;i<len;i++){
            int temp = in.nextInt();
            preMin = Math.min(preMin,temp);
            max = Math.max(max,temp-preMin);
        }
        System.out.println(max) ;
    }
}

二、OR26 最长回文子串

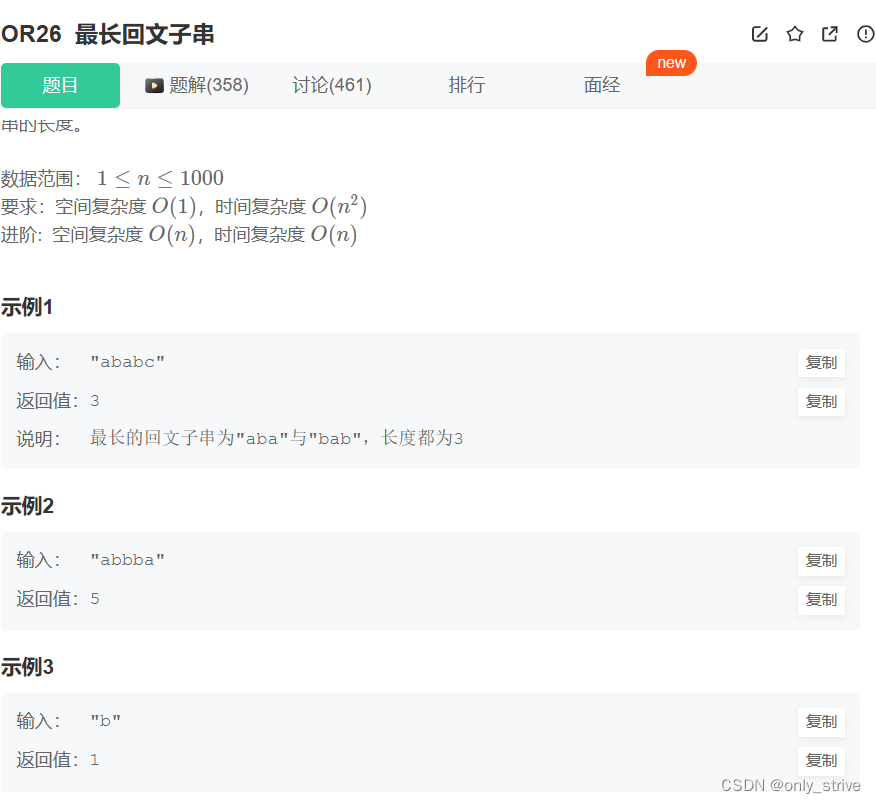
算法：中心扩展（注意奇数偶数回文的区别）
遍历中心点，每次遍历向两端扩展，直到不相等为止，长度为r-l-1；

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param A string字符串 
     * @return int整型
     */
    public int getLongestPalindrome (String A) {
        // write code here
        //中心扩展算法
        int max = 0;
        int len = A.length();
        int left = 0 ;
        int right = 0; 
        for(int i = 0;i<len;i++){
                //奇数回文串
            left = i-1;
            right = i+1;
            while(left>=0&&right<len){
                if(A.charAt(left)==A.charAt(right)){
                    left--;
                    right++;
                }else{
                    break;
                }
            }
            max = Math.max(max,right-left-1);
                //偶数回文串
             left = i;
            right = i+1;
            while(left>=0&&right<len){
                if(A.charAt(left)==A.charAt(right)){
                    left--;
                    right++;
                }else{
                    break;
                }
            }
            max = Math.max(max,right-left-1);
        }
        return max;
    }
}

三、NC369 [NOIP2002 普及组] 过河卒

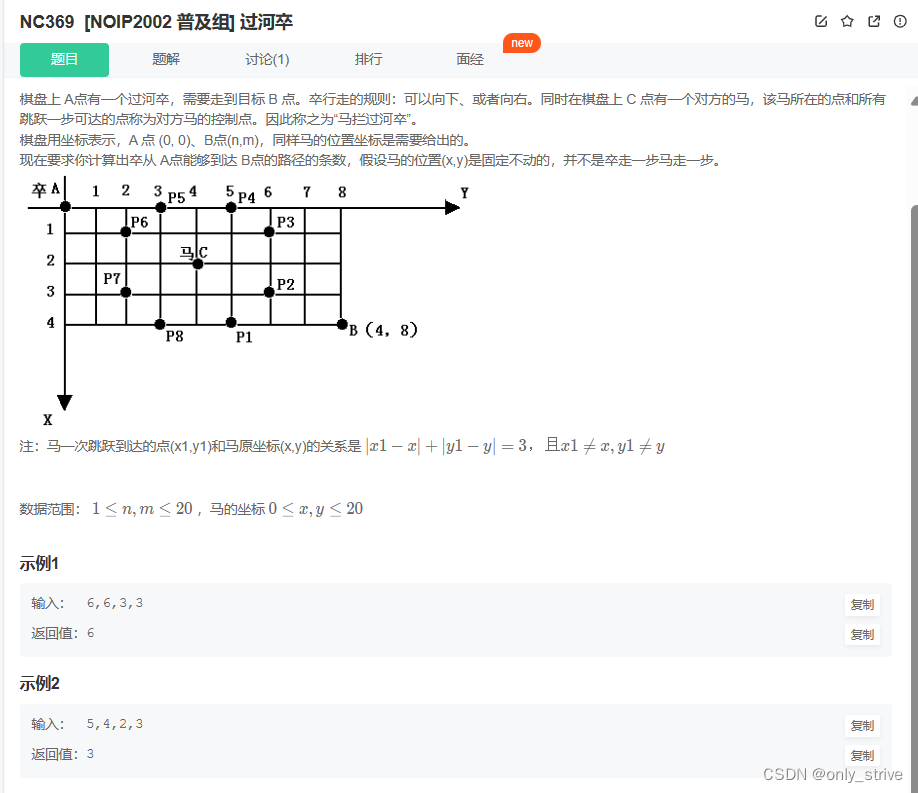
算法：动态规划-路径
1.状态表示
dp[i][j]表示：从[0,0]位置出发，到达dp[i,j]位置，一共有多少种方法
2.状态转移方程
dp[i,j] = dp[i-1,j]+dp[i,j-1];需要判断dp[i.j]位置
3.初始化
多加一行一列

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param n int整型 棋盘行数
     * @param m int整型 棋盘列数
     * @param x int整型 马的横坐标
     * @param y int整型 马的纵坐标
     * @return int整型
     */
    public int crossRiver (int n, int m, int x, int y) {
        // write code here
        int[][] dp = new int[n+2][m+2];
        dp[0][1] = 1;
        x+=1;
        y+=1;
        for(int i=1;i<=n+1;i++){
            for(int j =1;j<=m+1;j++){
                if(i!=x&&j!=y&&Math.abs(i-x)+Math.abs(j-y)==3||
                (i==x&&j==y)){
                    dp[i][j] = 0;
                }else{
                    dp[i][j] = dp[i-1][j]+dp[i][j-1];
                    // System.out.println(dp[i][j]);
                }
            }
        }
        return dp[n+1][m+1];
    }
}