目录

题目

离散时间系统的系统函数：H(z)=(3*z^3-5*z^2+10z)/(z^3-3*z^2+7*z-5)

 1，绘制该系统的零极点图 

1）零极点图

2）代码

2，判断系统的稳定性

1）判断结果

2）代码

3，试用MATLAB绘出该系统的幅频和相频特性曲线

1）幅频和相频特性曲线

2）代码

---

题目

离散时间系统的系统函数：H(z)=(3*z^3-5*z^2+10z)/(z^3-3*z^2+7*z-5)

 1，绘制该系统的零极点图 

要在MATLAB中绘制离散时间系统的零极点图，可以使用zplane函数：

步骤： 

1. 首先，将系统函数H(z)分解为分子和分母的多项式系数，然后将这些系数传递给zplane函数。
2. numerator中的最后一个系数是0，这是因为z^3的系数在分子中不存在，但是为了保持多项式的阶数一致，仍然需要将其包括在内，并设置为0。
3. 然后，使用zplane函数来绘制零极点图，并添加了标题和轴标签。
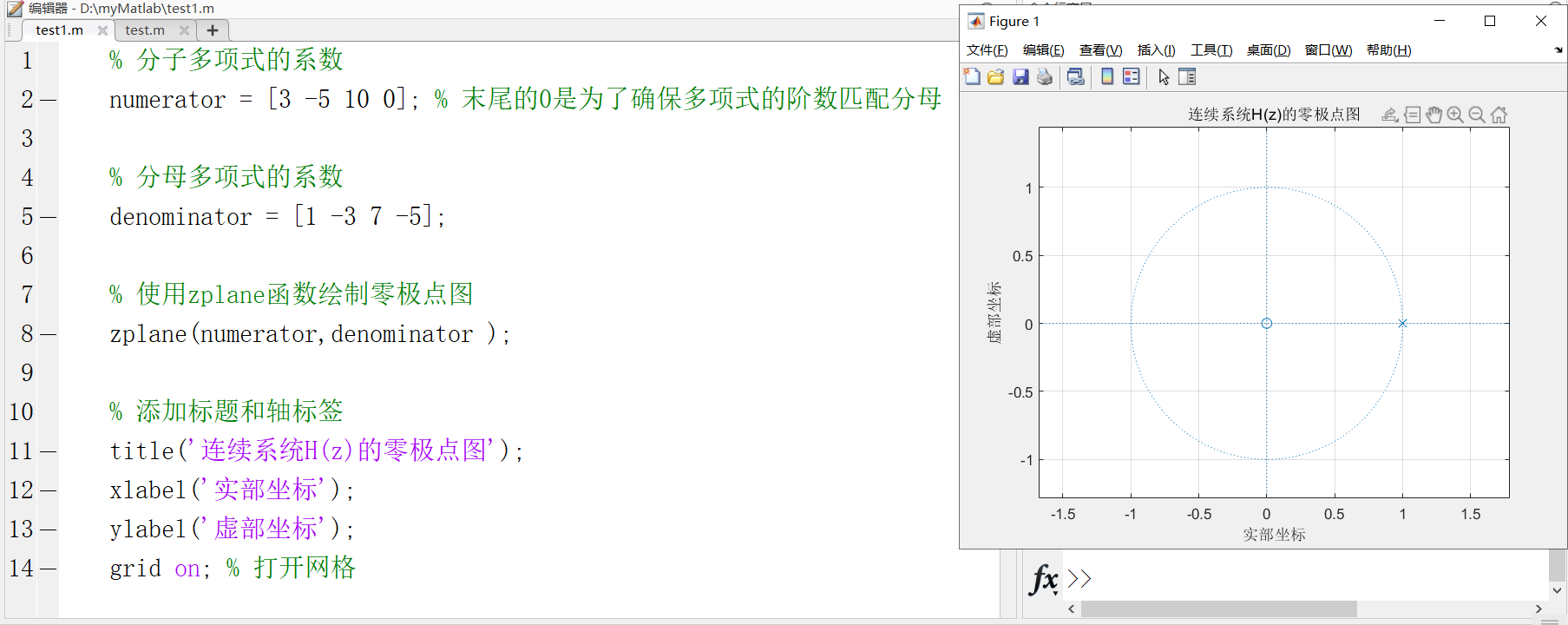
4. 最后，grid on命令用于开启网格，以便更清晰地查看图形：显示一个包含零点和极点的图。零点用“o”标记，极点用“x”标记。这些点位于复平面的相应位置上。

1）零极点图

2）代码

% 分子多项式的系数  
numerator = [3 -5 10 0]; % 末尾的0是为了确保多项式的阶数匹配分母  
  
% 分母多项式的系数  
denominator = [1 -3 7 -5];  
  
% 使用zplane函数绘制零极点图  
zplane(numerator,denominator );  
  
% 添加标题和轴标签  
title('连续系统H(z)的零极点图');  
xlabel('实部坐标');  
ylabel('虚部坐标');  
grid on; % 打开网格

2，判断系统的稳定性

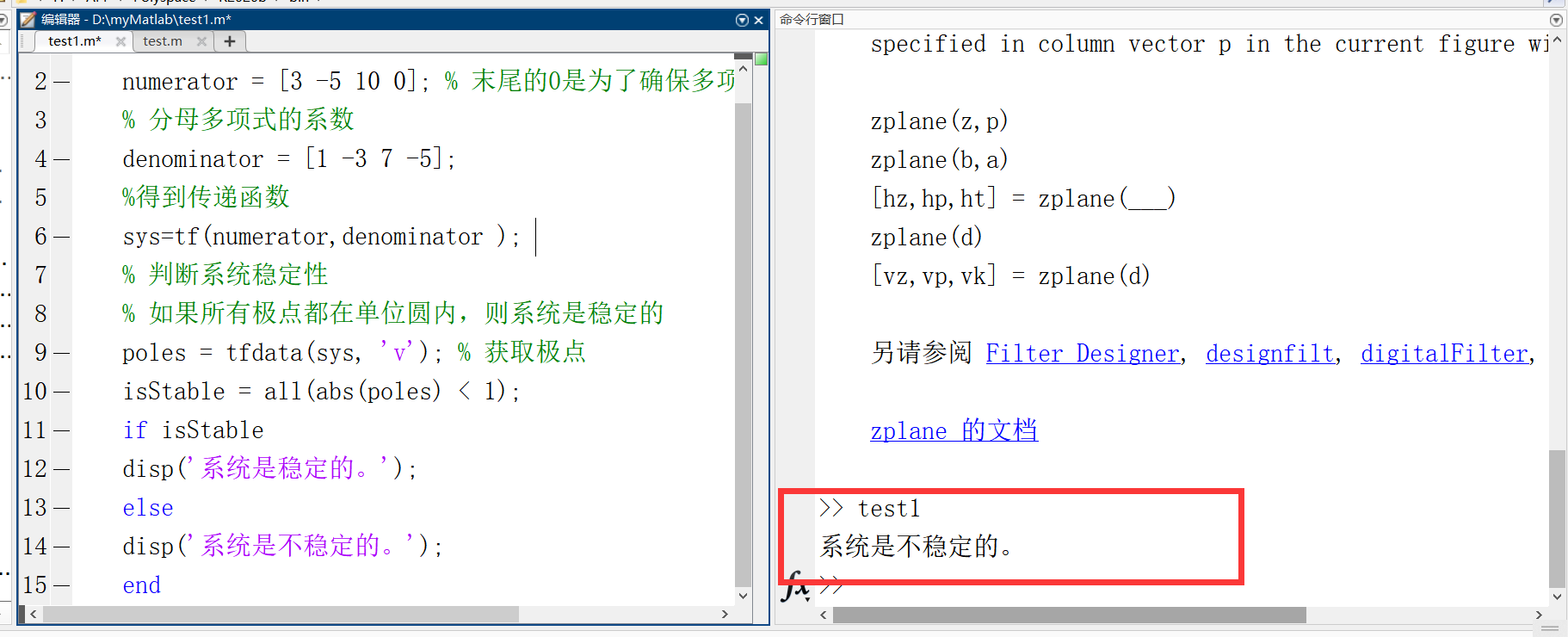
1）判断结果

2）代码

% 分子多项式的系数  
numerator = [3 -5 10 0]; % 末尾的0是为了确保多项式的阶数匹配分母  
% 分母多项式的系数  
denominator = [1 -3 7 -5];  
%得到传递函数 
sys=tf(numerator,denominator ); 
% 判断系统稳定性
% 如果所有极点都在单位圆内，则系统是稳定的
poles = tfdata(sys, 'v'); % 获取极点
isStable = all(abs(poles) < 1);
if isStable
disp('系统是稳定的。');  % 输出到命令行窗口中
else
disp('系统是不稳定的。');
end  

3，试用MATLAB绘出该系统的幅频和相频特性曲线

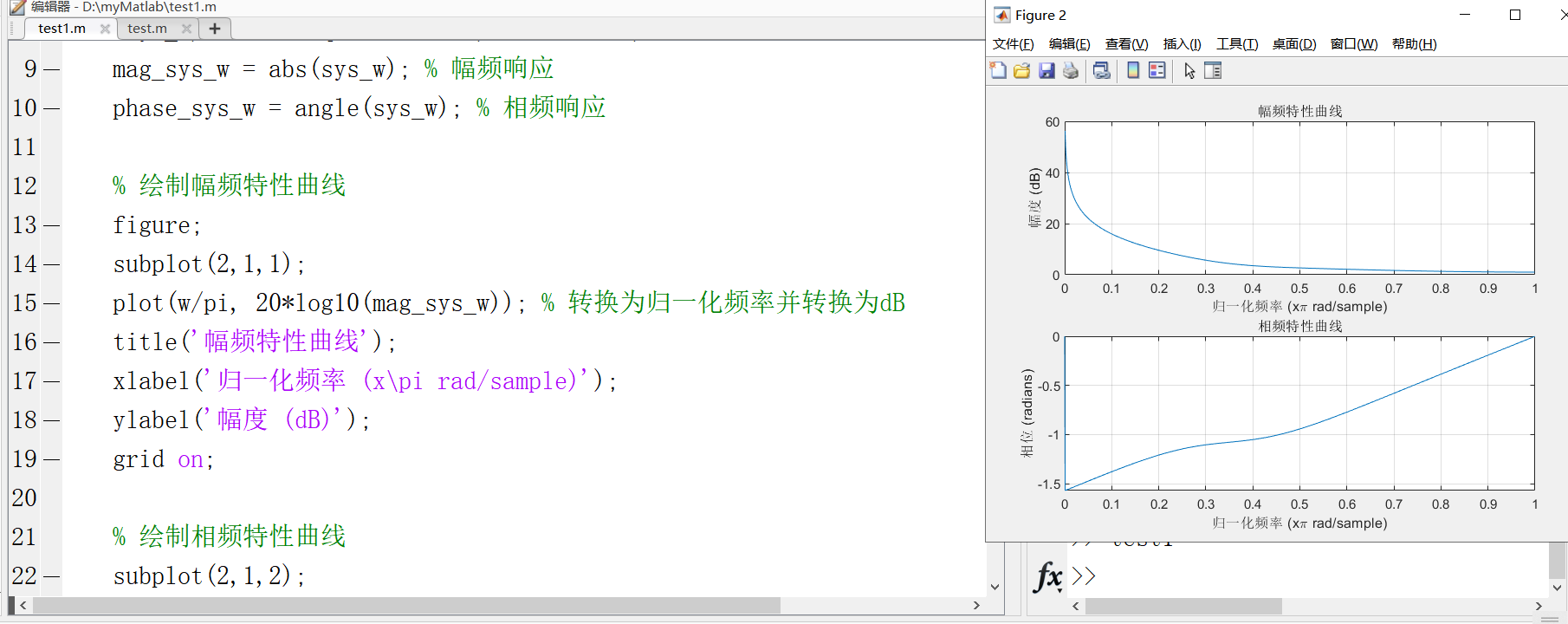
1）幅频和相频特性曲线

基础： 

• tfdata函数可以获取极点，并用来判断系统的稳定性。
• freqz函数用来计算频率响应，绘制幅频和相频特性曲线。

2）代码

% 分子多项式的系数  
numerator = [3 -5 10 0]; % 末尾的0是为了确保多项式的阶数匹配分母  
% 分母多项式的系数  
denominator = [1 -3 7 -5];  
%得到传递函数 
sys=tf(numerator,denominator ); 
% 绘制幅频和相频特性曲线
[sys_w, w] = freqz(numerator,denominator, 1024); % 计算频率响应，1024是频率点的数量
mag_sys_w = abs(sys_w); % 幅频响应
phase_sys_w = angle(sys_w); % 相频响应

% 绘制幅频特性曲线
figure;
subplot(2,1,1);
plot(w/pi, 20*log10(mag_sys_w)); % 转换为归一化频率并转换为dB
title('幅频特性曲线');
xlabel('归一化频率 (x\pi rad/sample)');
ylabel('幅度 (dB)');
grid on;

% 绘制相频特性曲线
subplot(2,1,2);
plot(w/pi, unwrap(phase_sys_w)); % 转换为归一化频率并使用unwrap函数处理相位跳变
title('相频特性曲线');
xlabel('归一化频率 (x\pi rad/sample)');
ylabel('相位 (radians)');
grid on;

 有问题请在评论区留言，1天8h在线。