目录
什么是深度和广度优先
图的深度优先遍历-城市地图
图的广度优先遍历-最少转机
什么是深度和广度优先
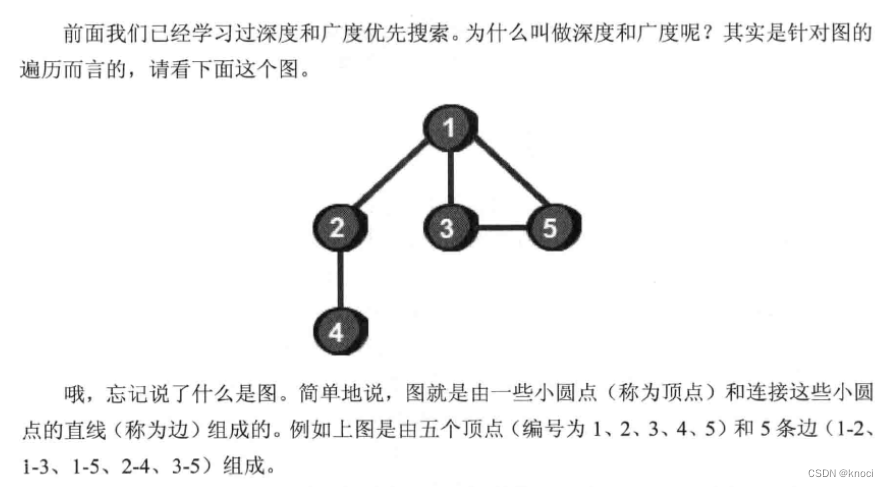
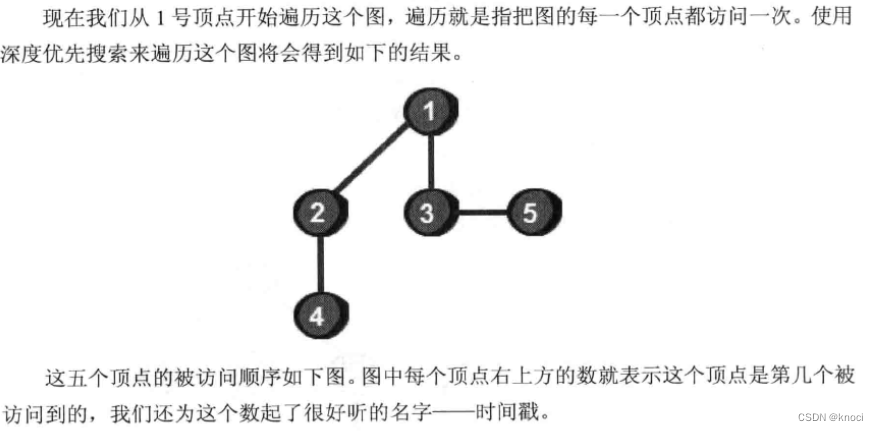
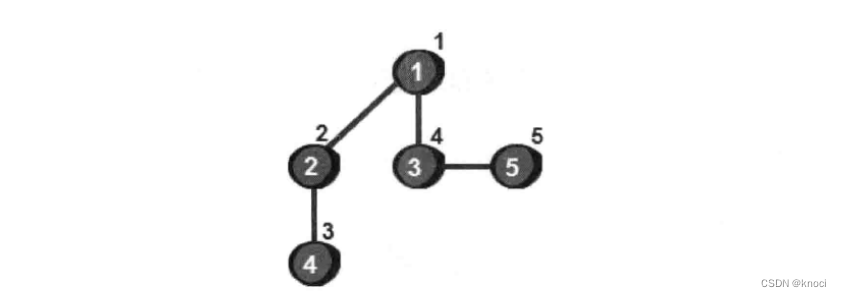
使用深度优先搜索来遍历这个图的过程具体是:
- 首先从一个未走到过的顶点作为起始顶点, 比如以1号顶点作为起点。
- 沿1号顶点的边去尝试访问其它未走到过的顶点, 首先发现2 号顶点还没有走到过, 于是来到了2 号顶点。
- 再以2 号顶点作为出发点继续尝试访问其它未走到过的顶点, 这样又来到了4号顶点。
- 再以4 号顶点作为出发点继续尝试访问其它未走到过的顶点。
- 但是, 此时沿4号顶点的边, 已经不能访问到其它未走到过的顶点了, 所以要返回到2号顶点。
- 返回到2号顶点后, 发现沿2 号顶点的边也不能再访问到其它未走到过的顶点。因此还需要继续返回到1号顶点。
- 再继续沿1号顶点的边看看还能否访问到其它未走到过的顶点。
- 此时又会来到3号顶点, 再以3号顶点作为出发点继续访问其它未走到过的顶点, 千是又来到5号顶点。
- 到此, 所有顶点都走到过了, 遍历结束。
深度优先遍历的主要思想就是:首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;没有未访问过的顶点时, 则回到上一个顶点, 继续试探访问别的顶点, 直到所有的顶点都被访问过。
显然, 深度优先遍历是沿着图的某一条分支遍历直到末端, 然后回溯, 再沿着另一条进行同样的遍历, 直到所有的顶点都被访问过为止。那这一过程如何用代码来实现呢?在讲代码实现之前我们先来解决如何存储一个图的问题。最常用的方法是使用一个二维数组e来存储, 如下。

上图二维数组中第i行第j列表示的就是顶点 i 到顶点 j 是否有边。1表示有边, ∞表示
没有边, 这里我们将自己到自己(即i等于j)设为0。我们将这种存储图的方法称为图的邻
接矩阵存储法。
注意观察会发现这个二维数组是沿主对角线对称的, 因为上面这个图是无向图。所谓无向阳指的就是图的边没有方向, 例如边1-5表示, 1号顶点可以到5号顶点, 5号顶点也可以到1号顶点。
接下来要解决的问题就是如何用深度优先搜索来实现遍历了。
void dfs(int cur) { // cur是当前所在的顶点编号
printf("%d. ", cur);
sum++; // 每访问一个顶点s就加1
if (sum == n) return; // 所有的顶点都已经访问过则直接退出
for (i = 1; i <= n; i++) { // 从1号顶点到n号顶点依次尝试,看哪些顶点与当前顶点cur有边相连
// 判断当前顶点cur到顶点i是否有边,并判断顶点i是否已访问过
if (e[cur][i] == 1 && book[i] == 0) {
// 标记顶点i已经访问过
book[i] = 1;
// 从顶点i再出发继续遍历
dfs(i);
}
}
return;
}在上面的代码中变揽cur存储的是当前正在遍历的顶点, 二维数组e存储的就是图的边(邻接矩阵), 数组book用来记录哪些顶点已经访问过, 变揽sum用来记录已经访问过多少个顶点, 变证n存储的是图的顶点的总个数。完整代码如下。
#include <stdio.h>
int book[101], sum, n, e[101][101];
void dfs(int cur) { // cur是当前所在的顶点编号
int i;
printf("%d ", cur);
sum++; // 每访问一个顶点,sum就加1
if (sum == n) return; // 所有的顶点都已经访问过则直接退出
for (i = 1; i <= n; i++) { // 从1号顶点到n号顶点依次尝试,看哪些顶点与当前顶点cur有边相连
// 判断当前顶点cur到顶点i是否有边, 并判断顶点i是否已访问过
if (e[cur][i] == 1 && book[i] == 0) {
// 标记顶点i已经访问过
book[i] = 1;
// 从顶点i再出发继续遍历
dfs(i);
}
}
return;
}
int main() {
int i, j, m, a, b;
scanf("%d %d", &n, &m);
// 初始化二维矩阵
for (i = 1; i <= n; i++) {
for (j = 1; j <= n; j++) {
if (i == j)
e[i][j] = 0;
else
e[i][j] = 99999999; // 我们这里假设999999999为正无穷
}
}
// 读入顶点之间的边
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1; // 这里是无向图,所以需要将e[b][a]也赋为1
}
// 从1号城市出发
book[1] = 1; // 标记1号顶点已访问
dfs(1); // 从1号顶点开始遍历
getchar();
getchar();
return 0;
}

广度优先遍历的主要思想就是:首先以一个未被访问过的顶点作为起始顶点,访问其所有相邻的顶点, 然后对每个相邻的顶点,再访问它们相邻的未被访问过的顶点,直到所有顶点都被访问过, 遍历结束。
代码实现如下:
#include <stdio.h>
int main() {
int i, j, n, m, a, b, cur;
int book[101] = {0}; // 使用数组初始化语法将book数组初始化为全0
int e[101][101];
int que[10001], head = 0, tail = 0; // 将队列初始化为0
scanf("%d %d", &n, &m);
// 初始化二维矩阵
for (i = 1; i <= n; i++) {
for (j = 1; j <= n; j++) {
if (i == j) {
e[i][j] = 0;
}
else {
e[i][j] = 99999999; // 假设999999999为正无穷
}
}
}
// 读入顶点之间的边
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1; // 无向图,需要双向赋值
}
// 从1号顶点出发,将1号顶点加入队列
que[tail] = 1;
tail++;
book[1] = 1; // 标记1号顶点已访问
// 当队列不为空时循环
while (head < tail) {
cur = que[head]; // 当前正在访问的顶点编号
// 从1~n依次尝试
for (i = 1; i <= n; i++) {
// 判断从顶点cur到顶点i是否有边,且顶点i是否已经访问过
if (e[cur][i] == 1 && book[i] == 0) {
// 如果从顶点cur到顶点i有边,并且顶点i没有被访问过,则将顶点i入队
que[tail] = i;
tail++;
book[i] = 1; // 标记顶点i已访问
}
}
// 如果tail大于n,则所有顶点都已经被访问过,退出循环
if (tail > n) {
break;
}
head++; // 顶点扩展结束后,head++,继续往下扩展
}
// 输出队列中的顶点编号
for (i = 0; i < tail; i++) {
printf("%d ", que[i]);
}
getchar();
getchar();
return 0;
}图的深度优先遍历-城市地图

我们可以创建一个5*5的邻接矩阵,如下图:
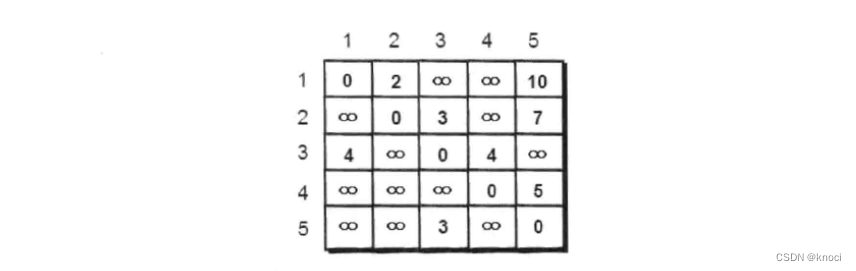
用book数组记录哪些城市已经走过,用全局变量min来更新每次找到的路径的最小值,代码实现如下:
#include <stdio.h>
int min = 99999999, book[101], n, e[101][101]; // 我们这里假设999999999为正无穷
// cur是当前所在的城市编号,dis是当前已经走过的路程
void dfs(int cur, int dis) {
int j;
// 如果当前走过的路程已经大于之前找到的最短路,则没有必要再往下尝试了,立即返回
if (dis > min)
return;
if (cur == n) // 判断是否到达了目标城市
{
if (dis < min) {
min = dis; // 更新最小值
return;
}
}
for (j = 1; j <= n; j++) { // 从1号城市到n号城市依次尝试
// 判断当前城市cur到城市j是否有路,并判断城市j是否在已走过的路径中
if (e[cur][j] != 99999999 && book[j] == 0) {
book[j] = 1; // 标记城市j已经在路径中
dfs(j, dis + e[cur][j]); // 从城市j再出发,继续寻找目标城市
book[j] = 0; // 之前一步探索完毕之后,取消对城市j的标记
}
}
}
int main() {
int i, j, m, a, b, c;
scanf("%d %d", &n, &m);
// 初始化二维矩阵
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j)
e[i][j] = 0;
else
e[i][j] = 99999999;
// 读入城市之间的道路
for (i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
e[a][b] = c;
}
// 从1号城市出发
book[1] = 1; // 标记1号城市已经在路径中
dfs(1, 0); // 1表示当前所在的城市编号,0表示当前已经走过的路程
printf("%d\n", min); // 打印1号城市到目标城市的最短路径
getchar();
getchar();
return 0;
}
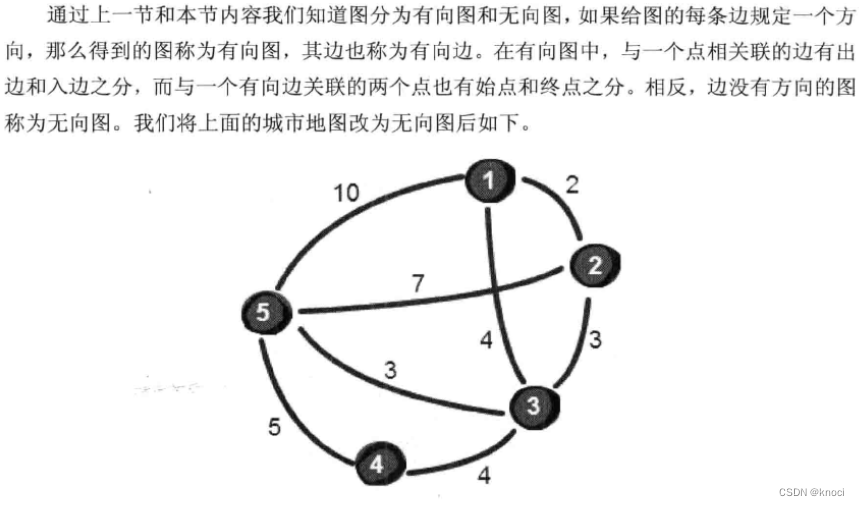

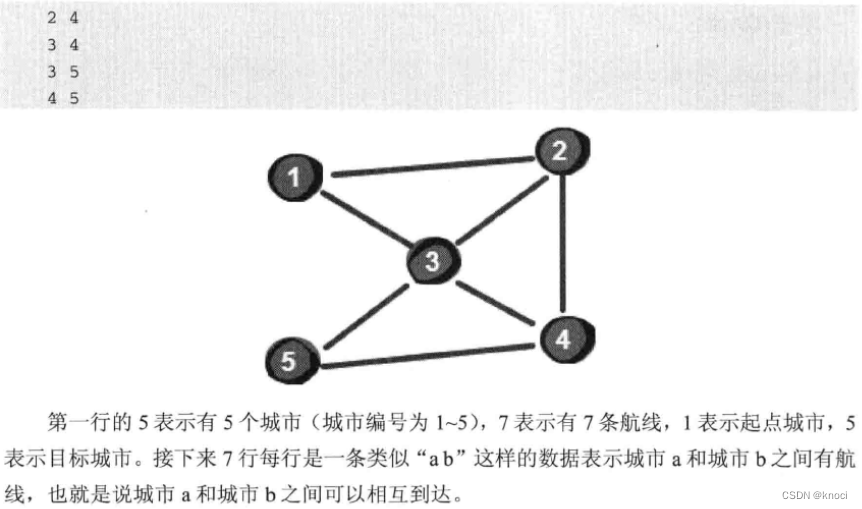
图的广度优先遍历-最少转机

#include <stdio.h>
struct note {
int x; // 城市编号
int s; // 转机次数
};
int main() {
struct note que[2501];
// 初始化
int e[51][51] = {0}, book[51] = {0};
int head, tail;
int i, j, n, m, a, b, cur, start, end, flag = 0;
scanf("%d %d %d %d", &n, &m, &start, &end);
// 初始化二维矩阵
for (i = 1; i <= n; i++) {
for (j = 1; j <= n; j++) {
if (i == j)
e[i][j] = 0;
else
e[i][j] = 99999999;
}
}
// 读入城市之间的航班
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
// 注:这里是无向图
e[a][b] = 1;
e[b][a] = 1;
}
// 队列初始化
head = 1;
tail = 1;
// 从start号城市出发,将start号城市加入队列
que[tail].x = start;
que[tail].s = 0;
tail++;
book[start] = 1; // 标记start号城市已在队列中
// 当队列不为空的时候循环
while (head < tail) {
cur = que[head].x; // 当前队列中首城市的编号
for (j = 1; j <= n; j++) { // 从1~n依次尝试
// 从城市cur到城市j是否有航班并且判断城市j是否已经在队列中
if (e[cur][j] != 99999999 && book[j] == 0) {
// 如果从城市cur到城市j有航班并且城市j不在队列中,则将城市j入队
que[tail].x = j;
que[tail].s = que[head].s + 1; // 转机次数+1
tail++;
// 标记城市j已经在队列中
book[j] = 1;
// 如果到达目标城市,停止扩展,任务结束,退出循环
if (que[tail].x == end) {
// 注意下面两句话的位置千万不要写颠倒了
flag = 1;
break;
}
}
}
if (flag == 1)
break;
head++; // 注意这地方,千万不要忘记当一个点扩展结束后,head++才能继续扩展
}
// 打印队列中末尾最后一个(目标城市)的转机次数
// 注意:tail是指向队列队尾(即最后一位)的下一个位置,所以这里要-1
printf("%d\n", que[tail - 1].s);
getchar();
getchar();
return 0;
}
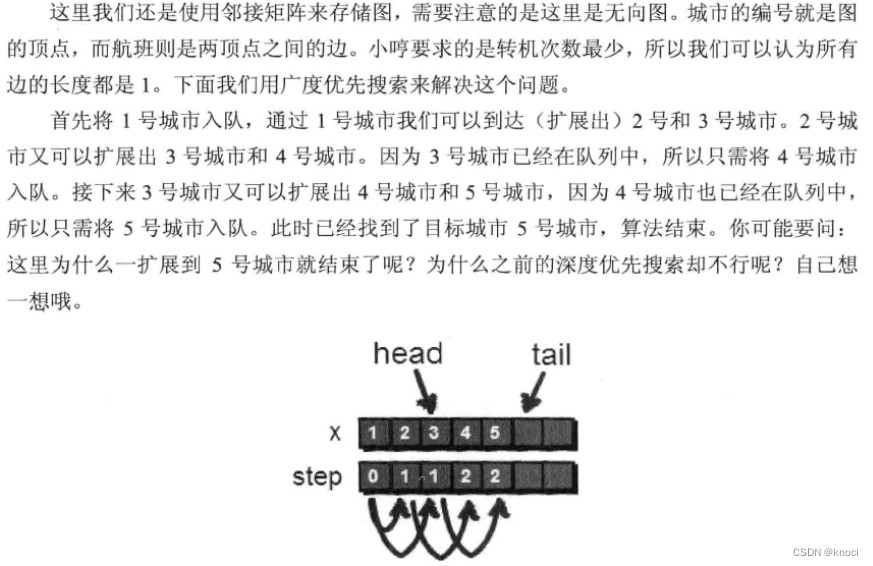
当然也可以使用深度优先搜索解决, 但是这里用广度优先搜索会更快。广度优先搜索更
加适用于所有边的权值相同的情况。