最小路径和

• 给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

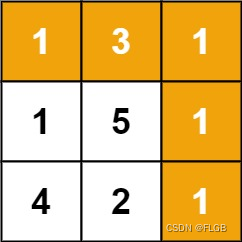
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

解题思路

• 1、使用动态规划求解，定义一个二维数组dp，其中dp[i][j]表示从左上角到达网格的第i行第j列位置的最小路径和。
• 2、初始化dp数组，将第一行和第一列的所有元素都进行累加，即
  dp[i][0] = grid[i][0] + dp[i-1][0]，dp[0][j] = grid[0][j] + dp[0][j-1]。
• 3、对于其他位置，根据状态转移方程dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])，即当前位置的最小路径和等于当前位置的值加上上方位置和左方位置的最小路径和中的较小值。
• 4、最终返回dp[m-1][n-1]即可，表示从左上角到达右下角的最小路径和。

Java实现

public class MinimumPathSum {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;

        // 初始化dp[0][0]
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];

        // 初始化第一行
        for (int j = 1; j < n; j++) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }

        // 初始化第一列
        for (int i = 1; i < m; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }

        //计算最小路径
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }

        return dp[m - 1][n - 1];
    }

    public static void main(String[] args) {
        MinimumPathSum solution = new MinimumPathSum();
        int[][] grid = {{1, 3, 1}, {1, 5, 1}, {4, 2, 1}};
        System.out.println("Minimum path sum: " + solution.minPathSum(grid)); // Output: 7
    }
}

时间空间复杂度

• 时间复杂度：遍历了一次二维数组dp，时间复杂度为O(m*n)，其中m为网格的行数，n为网格的列数。

• 空间复杂度：使用了一个二维数组dp，空间复杂度为O(m*n)。