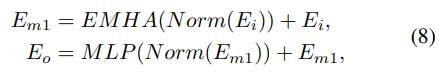简便算法的原理

我们发现乘法一共只有两种，分别是两因数和为奇数与和为偶数。和为奇数的两数之和总可以拆成两个相邻的数（如 $13=6+7$），和为偶数的两数之和总可以拆成两个相同的数（如 $12=6+6$）。不难发现和相同的一组数的乘积是有某种规律的。

1. 先看和为偶数的：
   

不难发现，与最大值的因数相差 $n$ 时，乘积相差 $n^2$。

2.再看和为奇数的：

与最大值的因数中较大的数相差 $n$ 时，乘积相差 $n(n+1)$。

算法的实现

可以将原算式转化为和相同的其他算式（最好是凑整），用两个算式与最大值的关系进行调整。
基本公式：原算式 = 新算式 + 新算式与最大值的差 - 原算式与最大值的差。同样分为和为奇数与和为偶数分别进行推导。本部分只推导调整值（即新算式与最大值的差 - 原算式与最大值的差）。

1.和为偶数

这部分相对简单，所以放在了前面。
设最大值时的因数为 $x$，原算式较大因数为 $b$，调整后的较大数与原较大数的差为 $y$（如原式为 $41\times 87$，新式为 $28\times 100$，则 $y=13$）。根据上面的结论，原算式与最大值的差为 $(b-x{)}^2$，新算式与最大值的差为 $(b+y-x{)}^2$。则调整值为 $(b+y-x{)}^2-(b-x{)}^2=y[2(b-x)+y]$。

2.和为奇数

设最接近时较大数为 $x$，$b,y$ 定义同上。原算式与最大值的差为 $(b-x)(b-x+1)$，新算式与最大值的差为 $(b+y-x)(b+y-x+1)$。调整值为 $(b+y-x)(b+y-x+1)-(b-x)(b-x+1)=y(b-x)+y(b-x+1)+y^2=y[2(b-x)+y+1]$。

3.总结及注意事项

1. 当调整向远离最大值方向进行时 $y$ 为正，向靠近最大值方向进行时 $y$ 为负。
2. 两个基本公式：
   和为偶数时：原算式=新算式+$y[2(b-x)+y]$。
   和为奇数时：原算式=新算式+$y[2(b-x)+y+1]$。
   3.公式的拓展：
   如果令 $x$ 为最大值时较小的因数，$a$ 为原算式中较小的因数，则两个调整值也可分别写作 $y[2(x-a)+y]$ 以及 $y[2(x-a)+y+1]$。

实战演练

计算 $578\times 739$。
step 1：判断，和为奇数，$x=\lceil \frac{578+739}{2}\rceil =659$。
step 2：写出新算式，新算式可为 $517\times 800=413600$，此时 $y=61$。
step 3：计算调整值，调整值为 $61\times [2\times (739-659)+61+1]=61\times 222=13542$。
step 4：加和，原式的结果为 $413600+13542=427142$。
这个方法 100% 有效，因为是经过数学推导得到的。背下两组公式，相信你的计算速度会有很大提升。