鲁棒局部均值分解（RLMD）附Matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法神经网络预测雷达通信无线传感器

信号处理图像处理路径规划元胞自动机无人机电力系统

⛄ 内容介绍

局部均值分解是一种信号处理方法，旨在从信号中提取出一组纯调频信号和包络信号的“最佳拟合”乘积函数( product functions，PF) ，通过数学迭代循环可以得到所有的 PF 分量，进而进行信号分析。对于信号 x( t) ，其分解过程如下。

⛄ 完整代码

function [pfs, ams, fms, ort, fvs, iterNum] = RLMD(x,varargin)

% Robust Local Mean Decomposition (RLMD)

% ERPHM Code

% 2017-06-11 Created by Dr.Zhiliang Liu, Deng Pan and Yaqiang Jin.

% If you have any questions, please contact us via Zhiliang_Liu@uestc.edu.cn

% This funcion perform the local mean decompose(LMD) on the input signal, and

% return the product function (pfs), and their corresponding instantaneous

% amplitude(ams) and frequency modulation signal(fms).

% SYNTAX:

% pfs = lmd_liu(x);

% [pfs, ams, fms, ort] = lmd_liu(x);

% [pfs, ams, fms, ort] = lmd_liu(x,options);

% [pfs, ams, fms, ort] = lmd_liu(x,'option_name1',option_value1,....);

% INPUTS:

% [1] x: a row signal vecter which you want to perform LMD.

% [2] option: a struct contains options' name(option_name) and

% corresponding values(option_value).

% [2.1] 'display'

% plot PFs, AMs and FMs or not,1 plot,0 do not.

% default: 0

% [2.2] 'max_iter'

% max number of iterations in one pf sift procedure.

% default: 30

% [2.3] 'max_pfs'

% max number of pfs obtained in lmd procedure.

% default: 10

% OUTPUTS

% [1] pfs

% Product Function(PF) Matrix of which each row is a PF and the last

% row is the residual signal.

% [2] ams

% amplitude modulation signal of each PF.

% [3] fms

% frequency modulation signal of each PF.

% [4] iterNum

% iteration times for each PF.

% [5] fvs

% objective funciton values

% [6] ort

% index of orthogonality

% REFERENCE

% [1] Zhiliang Liu, Yaqiang Jin, Ming J. Zuo, and Zhipeng Feng. Time-frequency

% representation based on robust local mean decomposition for multi-component

% AM-FM signal analysis. Mechanical Systems and Signal Processing. 95: 468-487, 2017.

% [2] Smith J S. The local mean decomposition and its application to EEG

% perception data[J]. Journal of the Royal Society Interface, 2005,

% 2(5): 443-454.

% [3] G. Rilling, P. Flandrin and P. Goncalves. On empirical mode

% decomposition and its algorithms. IEEE-EURASIP Workshop on Nonlinear

% Signal and Image Processing NSIP-03, Grado (I), June 2003

% % EXAMPLE:

% clc;close all;clear;

% fs = 10000; % sampling frequency

% N = 30000; % data amount

% t = (1:N)/fs; % time vector

% x1 = (2+cos(2*pi*0.5*t)).*cos(2*pi*5*t+15*t.^2);

% x2 = cos(2*pi*2*t);

% x = x1+x2;

% options.display = 1;

% options.max_iter = 30;

% options.max_pfs = 10;

% [pf3, ams3, fms3, ort3] = lmd_public(x,options);

% figure;

% subplot(2,1,1),plot(t,x1);

% subplot(2,1,2),plot(t,x2);

% Input arguments initialization

[x, display, stop_thre, sifting_stopping_mode, max_iter, max_pfs, smooth_mode,...

ma_span, ma_iter_mode, extd_r, x_energy, pfs, ams, fms, iterNum, fvs]...

= initial(x,varargin{:});

% Initialize main loop

i = 0;

xs = x; % copy x to xs for sifting process, reserve original input as x.

nx = length(x);

while i < max_pfs && ~stoplmd(xs, x_energy) % outer loop for PF selection

i = i+1;

% initialize variables used in PF sifting loop

a_i = ones(1,nx);

s_j = zeros(max_iter,nx);

a_ij = zeros(max_iter, nx);

% PF sifting iteration loop

j = 0;

stop_sifting = 0;

s = xs;

while j < max_iter && ~stop_sifting % inner loop for sifting process

j = j+1;

[m_j, a_j, n_extr] = lmd_mean_amp(s, smooth_mode, ma_span, ma_iter_mode,...

extd_r);

% force to stop iter if number of extrema of s is smaller than 3.

if n_extr < 3

break;

end

h_j = s-m_j; % remove mean.

s = h_j./a_j; % demodulate amplitude.

a_i = a_i .* a_j; % mulitiply every ai

a_ij(j, :) = a_i;

s_j(j, :) = s;

[stop_sifting,fvs(i,:)] = is_sifting_stopping(a_j, j, fvs(i,:), sifting_stopping_mode, stop_thre);

end % sift iteration loop

switch sifting_stopping_mode

case {'liu'}

[~, opt0] = min(fvs(i,1:j)); % ***Critical Step***

opt_IterNum = min(j, opt0); % in case iteration stop for n_extr<3

% opt_IterNum = min(j-2, opt0);

otherwise

error('No specifications for sifting_stopping_mode.');

end

ams(i, :) = a_ij(opt_IterNum, :); % save each amplitude modulation function in ams.

fms(i, :) = s_j(opt_IterNum, :); % save each pure frequency modulation function in fms.

pfs(i, :) = ams(i, :).*fms(i, :); % gain Product Funcion.

xs = xs-pfs(i, :); % remove PF just obtained from input signal;

iterNum(i) = opt_IterNum; % record the iteration times taken by of each PF sifing.

end % main loop

pfs(i+1, :) = xs; % save residual in the last row of PFs matrix.

ams(i+1:end,:) = []; fms(i+1:end,:) = []; pfs(i+2:end,:) = []; fvs(i+1:end,:) = [];

ort = io(x, pfs);

% Output visualization

if display == 1

lmdplot(pfs, ams, fms, smooth_mode);

end

%--------------------------- built-in functions ---------------------------

% initialize signal and options

function [x, display, stop_thre, sifting_stopping_mode, max_iter, max_pfs, smooth_mode,...

ma_span, ma_iter_mode, extd_r, x_energy, pfs, ams, fms, iterNum, fvs]...

= initial(x,varargin)

% option fields(i.e. name)

optn_fields = {'display', 'stop_thre', 'sifting_stopping_mode', 'max_iter',...

'max_pfs', 'smooth_mode', 'ma_span', 'ma_iter_mode','extd_r', 'fix','fix_h'};

% set default options(def_opts)

def_optns.display = 0; % plot PFs.

def_optns.stop_thre = [0.005,0.7,0.05]; % sifting stopping thresholds for Rilling's criterion

def_optns.sifting_stopping_mode = 'liu'; % sifting stoppling optimizaion

def_optns.max_iter = 30; % max iteration number in a PF sifting process.

def_optns.max_pfs = 10; % max number of PFs.

def_optns.smooth_mode = 'ma'; % ma - moving average, spline - pchip.

def_optns.ma_span = 'liu'; % pdmax span method, see function ma_span.

def_optns.ma_iter_mode = 'fixed'; % fixed or dynamic span for iterate ma.

def_optns.extd_r = 0.2; % end extension length to original data.

optns = def_optns; % opts stores the final options.

% get user input options(in_opts)

if nargin == 1 % use default options(see above).

in_optns = def_optns;

elseif nargin == 2 && isstruct(varargin{1})

% 1st argument is x, 2nd is options in a struct.

in_optns = varargin{1};

elseif nargin > 2 % input options seperately.

try

in_optns = struct(varargin{:});

catch

error('wrong argmument syntax')

end

else

error('arguments error: maybe not enough or wrong syntax')

end

names = fieldnames(in_optns);% get input options' name and value

for k = names'

if ~any(strcmpi(char(k), optn_fields))

% find any wrong argument in syntax.

error(['bad option field name: ',char(k)])

end

if ~isempty(eval(['in_optns.',char(k)]))

% alter default option values with input, and empty input keep default.

eval(['optns.',lower(char(k)),' = in_optns.',char(k),';'])

end

display = optns.display;

stop_thre = optns.stop_thre;

sifting_stopping_mode = optns.sifting_stopping_mode;

max_iter = optns.max_iter;

max_pfs = optns.max_pfs;

smooth_mode = optns.smooth_mode;

ma_span = optns.ma_span;

ma_iter_mode = optns.ma_iter_mode;

extd_r = optns.extd_r;

% initialize x(input signal), x_energy, pf, ams, fms.

x = x(:)'; % make x a row vector.

nx = length(x);

x_energy = sum(x.^2); % energy = square summation.

ams = zeros(max_pfs,nx);

fms = zeros(max_pfs,nx);

pfs = zeros(max_pfs,nx);

iterNum = zeros(1,max_pfs);

fvs = zeros(max_pfs,max_iter);

% fix = opts.fix;

% fix_h = opts.fix_h;

% mask = opts.mask;

% ndirs = opts.ndirs;

% complex_version = opts.complex_version;

end

% Check if there are enough (3) extrema to continue the decomposition

function stop = stoplmd(x, x_energy)

[indmin,indmax] = extr(x);

peak = length(indmin) + length(indmax);

ratio = sum(x.^2)/x_energy;

stop = peak < 3 | ratio < 0.001;

end

% Compute mean function and amplitude function of x in LMD

function [m, a, n_extr] = lmd_mean_amp(x,smooth_mode,ma_span,ma_iter_mode,extd_r)

% find extremum indices

[indmin, indmax, ~] = extr(x);

% total amount of extrema

n_extr = length(indmin)+length(indmax);

if n_extr < 3

m = [];

a = [];

return

end

% extend original data to refrain end effect

% ext_indmin(max) contains the end point's index

[ext_indmin,ext_indmax,ext_x,cut_index] = extend(x, indmin, indmax, extd_r);

% preparation

m0 = zeros(1,length(ext_x));

a0 = zeros(1,length(ext_x));

ind_extextr = sort([ext_indmin, ext_indmax]);

% compute local mean and amplititude sequence

switch smooth_mode

case 'ma'

for k = 1:length(ind_extextr)-1

subm1 = ind_extextr(k);

subm2 = ind_extextr(k+1);

m0(subm1:subm2) = 0.5*(ext_x(subm1)+ext_x(subm2));

a0(subm1:subm2) = 0.5*abs(ext_x(subm1)-ext_x(subm2));

end

[span, smax] = getBestSpan(ind_extextr, ext_x, ma_span);

% iterative moving average

m = itrma(m0, ma_iter_mode, span, smax, ma_span);

a = itrma(a0, ma_iter_mode, span, smax, ma_span);

m = m(:)'; % make m a row vector

a = a(:)';

% cut extension

m = m(1, cut_index(1):cut_index(2));

a = a(1, cut_index(1):cut_index(2));

otherwise

error('No specifications for smooth_mode.');

end

% Moving average span selection

% return the best span of moving average

function [span, smax] = getBestSpan(ind_extr, x, ma_span)

% ind_extr - indices of extremum of x

% x - data;

x_extr = x(ind_extr);

% 0 elements' indices of eql_extr are the first indices of identical

% maximum ,or minimum, pairs

eql_extr = x_extr(3:end)-x_extr(1:end-2);

% delete the extremum indecies between two identical maximum(minimum)

ind_extr(find(eql_extr == 0)+1) = [];

% vector contains all steps of local mean

step_vec = ind_extr(2:end)-ind_extr(1:end-1)+1;

smax = max(step_vec);

smean = mean(step_vec);

switch ma_span

case 'liu'

[density,xmesh] = histcounts(step_vec,'Normalization','probability');

xmesh = xmesh(1:end-1)+diff(xmesh)/2;

span_c = sum(xmesh.*density);

span_std = sqrt(sum((xmesh-span_c).^2.*density));

span = ceil(span_c + 3*span_std);

otherwise

error('No specifications for ma_span.');

end

span = ceil(span);

span = span+1-mod(span,2); % force span to be odd

end

% Iterative moving average dynamic step

function x = itrma(x, ma_iter_mode, span, smax, ma_span)

x = smooth(x, span);

nm = length(x);

switch ma_iter_mode

case 'fixed' % stick step

cntr = 0; % count times of moving average

max_c = ceil(smax/span)*15; % theoretic

% max_c = ceil(smax/(span-1));

% nm = length(x);

k = (span+1)/2;

kmax = nm - (span-1)/2;

while (k < kmax) && (cntr < max_c) % find flat step

if x(k) == x(k+1);

x = smooth(x, span);

cntr = cntr+1;

k = k-1;

end

k = k+1;

end

% while ~isempty(find(diff(x)==0)) && (cntr < max_c)

% % find(diff(x)==0)

% x = smooth(x, span);

% cntr = cntr+1;

% end

otherwise

error('No specifications for ma_iter_mode.');

end

% Extend original data to refrain end effect

% ** Modified on emd by G.Rilling and P.Flandrin

% ** http://perso.ens-lyon.fr/patrick.flandrin/emd.html

function [ext_indmin, ext_indmax, ext_x, cut_index] = extend(x, indmin,...

indmax, extd_r)

if extd_r == 0 % do not extend x

ext_indmin = indmin;

ext_indmax = indmax;

ext_x = x;

cut_index = [1,length(x)];

return

end

nbsym = ceil(extd_r*length(indmax)); % number of extrema in extending end

xlen = length(x);

t = 1:xlen;

% boundary conditions for interpolations :

% left end extend

if indmax(1) < indmin(1) % first extremum is maximum

if x(1) > x(indmin(1)) % first point > first min extremum

lmax = fliplr(indmax(2:min(end,nbsym+1)));

lmin = fliplr(indmin(1:min(end,nbsym)));

lsym = indmax(1);

else % first point < first min extremum

lmax = fliplr(indmax(1:min(end,nbsym)));

lmin = [fliplr(indmin(1:min(end,nbsym-1))),1];

lsym = 1;

end

else % first extremum is minimum

if x(1) < x(indmax(1)) % first point < first maximum

lmax = fliplr(indmax(1:min(end,nbsym)));

lmin = fliplr(indmin(2:min(end,nbsym+1)));

lsym = indmin(1);

else % first point > first minimum

lmax = [fliplr(indmax(1:min(end,nbsym-1))),1];

lmin = fliplr(indmin(1:min(end,nbsym)));

lsym = 1;

end

% right end extension

if indmax(end) < indmin(end) % last extremum is minimum

if x(end) < x(indmax(end)) % last point < last maximum

rmax = fliplr(indmax(max(end-nbsym+1,1):end));

rmin = fliplr(indmin(max(end-nbsym,1):end-1));

rsym = indmin(end);

else % last point > last maximum

rmax = [xlen, fliplr(indmax(max(end-nbsym+2,1):end))];

rmin = fliplr(indmin(max(end-nbsym+1,1):end));

rsym = xlen;

end

else % last extremum is maximum

if x(end) > x(indmin(end)) % last point > last minimum

rmax = fliplr(indmax(max(end-nbsym,1):end-1));

rmin = fliplr(indmin(max(end-nbsym+1,1):end));

rsym = indmax(end);

else % last point < last minimum

rmax = fliplr(indmax(max(end-nbsym+1,1):end));

rmin = [xlen, fliplr(indmin(max(end-nbsym+2,1):end))];

rsym = xlen;

end

tlmin = 2*t(lsym)-t(lmin);

tlmax = 2*t(lsym)-t(lmax);

trmin = 2*t(rsym)-t(rmin);

trmax = 2*t(rsym)-t(rmax);

% in case symmetrized parts do not extend enough

if tlmin(1) > t(1) || tlmax(1) > t(1)

if lsym == indmax(1)

lmax = fliplr(indmax(1:min(end,nbsym)));

else

lmin = fliplr(indmin(1:min(end,nbsym)));

end

if lsym == 1

error('bug')

end

lsym = 1;

% tlmin = 2*t(lsym)-t(lmin);

% tlmax = 2*t(lsym)-t(lmax);

end

if trmin(end) < t(xlen) || trmax(end) < t(xlen)

if rsym == indmax(end)

rmax = fliplr(indmax(max(end-nbsym+1,1):end));

else

rmin = fliplr(indmin(max(end-nbsym+1,1):end));

end

if rsym == xlen

error('bug')

end

rsym = xlen;

% trmin = 2*t(rsym)-t(rmin);

% trmax = 2*t(rsym)-t(rmax);

end

l_end = max(max(lmax, lmin));

r_end = min(min(rmax, rmin));

new_lmax = l_end+1-lmax;

new_lmin = l_end+1-lmin;

new_rmax = rsym-rmax;

new_rmin = rsym-rmin;

lx_length = l_end-lsym;

lx = fliplr(x(lsym+1:l_end));

rx = fliplr(x(r_end:rsym-1));

ext_x = [lx, x(lsym:rsym), rx];

ext_indmin = [new_lmin,indmin+lx_length-lsym+1,new_rmin+lx_length-lsym+1+...

rsym];

ext_indmax = [new_lmax,indmax+lx_length-lsym+1,new_rmax+lx_length-lsym+1+...

rsym];

% Index for cutting extension of x

cut_index = [lx_length-lsym+2, length(x)+lx_length-lsym+1];

end

% sifting stopping criterion

function [stop_sifting,fv_i] = is_sifting_stopping(a_j, j, fv_i, sifting_stopping_mode, stop_thre)

base = ones(size(a_j)); % base line is y = 1.

% df = abs(a_j - base); % difference between a_i and baseline.

df = (a_j - base);

switch sifting_stopping_mode

case 'liu' % local optimal iteration.

fv_i(j) = rms(df)+abs(kurtosis(df)-3);

% fv_i(j) = rms(df)+(kurtosis(df)-3);

% global temp;

% temp(j,:) = [rms(df),kurtosis(df)];

if j >= 3

if ((fv_i(j) >= fv_i(j-1)) && (fv_i(j-1) >= fv_i(j-2)))

stop_sifting = 1;

return;

end

otherwise

error('No specifications for sifting_stopping_mode.');

end

stop_sifting = 0;

end

% Extracts the indices of extrema

% ** Copied from emd toolbox by G.Rilling and P.Flandrin

% ** http://perso.ens-lyon.fr/patrick.flandrin/emd.html

function [indmin, indmax, indzer] = extr(x)

m = length(x);

if nargout > 2

x1 = x(1:m-1);

x2 = x(2:m);

indzer = find(x1.*x2<0);

if any(x == 0)

iz = find( x==0 );

% indz = [];

if any(diff(iz)==1)

zer = x == 0;

dz = diff([0 zer 0]);

debz = find(dz == 1);

finz = find(dz == -1)-1;

indz = round((debz+finz)/2);

else

indz = iz;

end

indzer = sort([indzer indz]);

end

d = diff(x);

n = length(d);

d1 = d(1:n-1);

d2 = d(2:n);

indmin = find(d1.*d2<0 & d1<0)+1;

indmax = find(d1.*d2<0 & d1>0)+1;

% when two or more successive points have the same value we consider only

% one extremum in the middle of the constant area (only works if the signal

% is uniformly sampled)

if any(d==0)

imax = [];

imin = [];

bad = (d==0);

dd = diff([0 bad 0]);

debs = find(dd == 1);

fins = find(dd == -1);

if debs(1) == 1

if length(debs) > 1

debs = debs(2:end);

fins = fins(2:end);

else

debs = [];

fins = [];

end

if ~isempty(debs)

if fins(end) == m

if length(debs) > 1

debs = debs(1:(end-1));

fins = fins(1:(end-1));

else

debs = [];

fins = [];

end

lc = length(debs);

if lc > 0

for k = 1:lc

if d(debs(k)-1) > 0

if d(fins(k)) < 0

% imax = [imax round((fins(k)+debs(k))/2)];

end

else

if d(fins(k)) > 0

% imin = [imin round((fins(k)+debs(k))/2)];

end

if ~isempty(imax)

indmax = sort([indmax imax]);

end

if ~isempty(imin)

indmin = sort([indmin imin]);

end

% Compute the index of orthogonality

% ** Copied from emd toolbox by G.Rilling and P.Flandrin

% ** http://perso.ens-lyon.fr/patrick.flandrin/emd.html

function ort = io(x,pfs)

% ort = IO(x,pfs) computes the index of orthogonality

% inputs : - x : analyzed signal

% - pfs : production function

n = size(pfs,1);

s = 0;

for i = 1:n

for j =1:n

if i~=j

s = s + abs(sum(pfs(i,:).*conj(pfs(j,:)))/sum(x.^2));

end

ort = 0.5*s;

end

% Plot PF, Amplititude Signal and FM Signal

function lmdplot(pfs, ams, fms, smooth_mode)

t = 1:size(pfs,2);

pfn = size(pfs,1);

figure

for pfi = 1:pfn

subplot(pfn,1,pfi);

plot(t,pfs(pfi,:));

if pfi < pfn

title(['PF',num2str(pfi),' (',smooth_mode,')']);

else

title(['Residual',' (',smooth_mode,')']);

end

figure

for ai = 1:pfn-1

subplot(pfn-1,1,ai);

plot(t,ams(ai,:));

title(['Amplitude Signal',num2str(ai),' (',smooth_mode,')']);

end

figure

for fsi = 1:pfn-1

subplot(pfn-1,1,fsi);

plot(t,fms(fsi,:));

title(['FM Signal',num2str(fsi),' (',smooth_mode,')']);

end

% 主函数

% EXAMPLE:

clc;

clear;

close all;

fs = 10000; % sampling frequency

N = 30000; % data amount

t = (1:N)/fs; % time vector

x1 = (2+cos(2*pi*0.5*t)).*cos(2*pi*5*t+15*t.^2);

x2 = cos(2*pi*2*t);

x = x1+x2;

options.display = 1;

options.max_iter = 30;

options.max_pfs = 10;

[pf3, ams3, fms3, ort3] = RLMD(x,options);

figure;

subplot(2,1,1),plot(t,x1);

subplot(2,1,2),plot(t,x2);

⛄ 运行结果

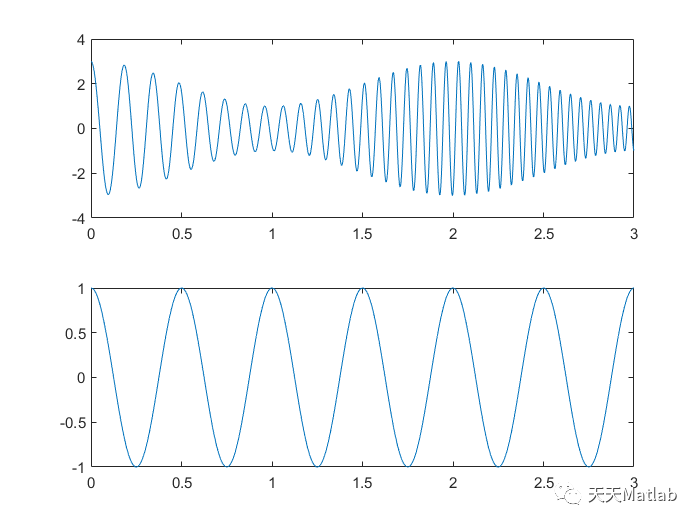
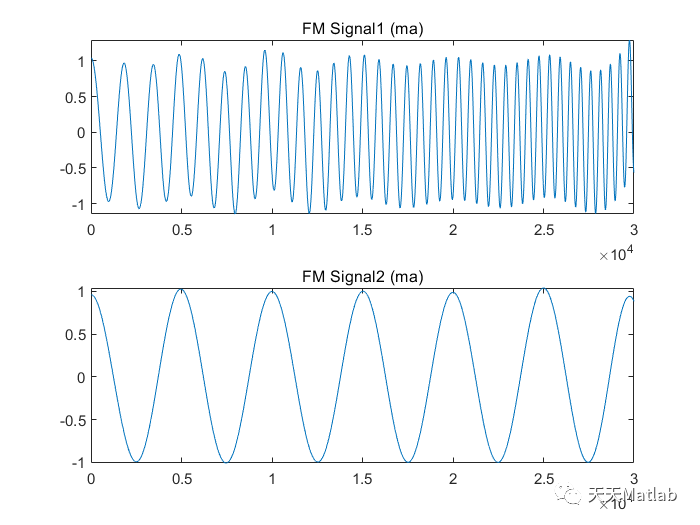
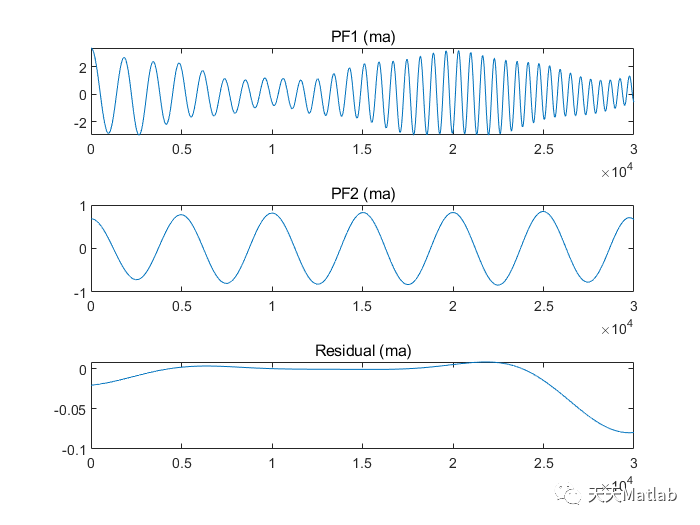
⛄ 参考文献

[1]林近山, 窦春红. 一种基于局部均值分解滤波的包络分析方法:, CN106198010B[P]. 2018.

[1]陈志刚, 赵志川, 钟新荣,等. 基于鲁棒局部均值分解与二阶瞬态提取变换的滚动轴承故障诊断[J]. 科学技术与工程, 2022, 22(1):157-165.

❤️ 关注我领取海量matlab电子书和数学建模资料

❤️部分理论引用网络文献，若有侵权联系博主删除