Java数据结构-堆和优先级队列

news2024/10/7 10:23:01

目录

  • 1. 相关概念
  • 2. PriorityQueue的实现
    • 2.0 搭建整体框架
    • 2.1 堆的创建和调整
    • 2.2 插入元素
    • 2.3 出堆顶元素
  • 3. 全部代码（包含大根堆和小根堆）
  • 4. PriorityQueue的使用
  • 5. Top-K问题

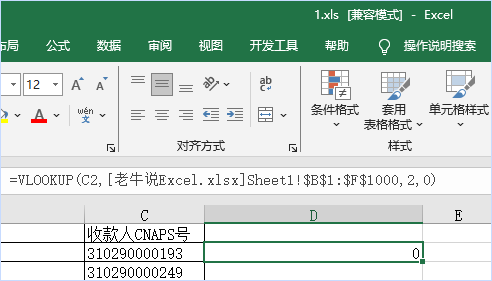
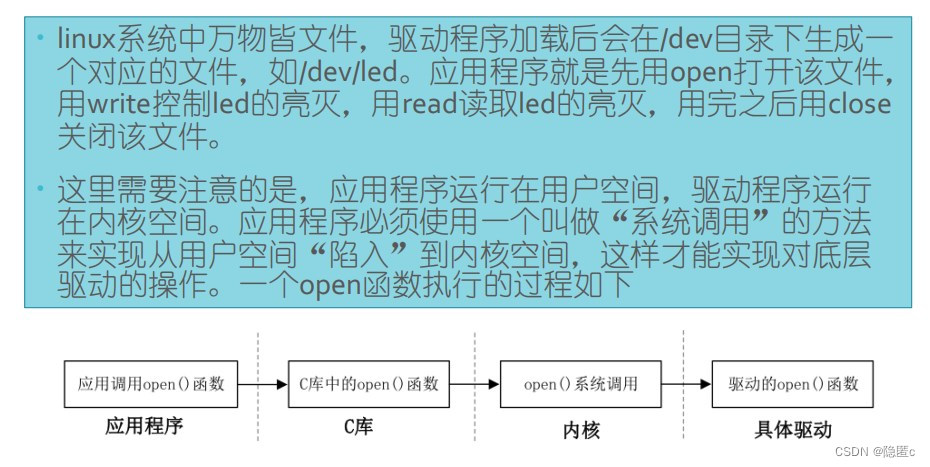
之前我们学习的二叉树的存储方式是链式存储，（不清楚的可以看这篇哦： 二叉树），而堆是二叉树的另一种存储方式：顺序存储，jdk1.8中的优先级队列： PriorityQueue 的底层就是使用了堆这种数据结构

1. 相关概念

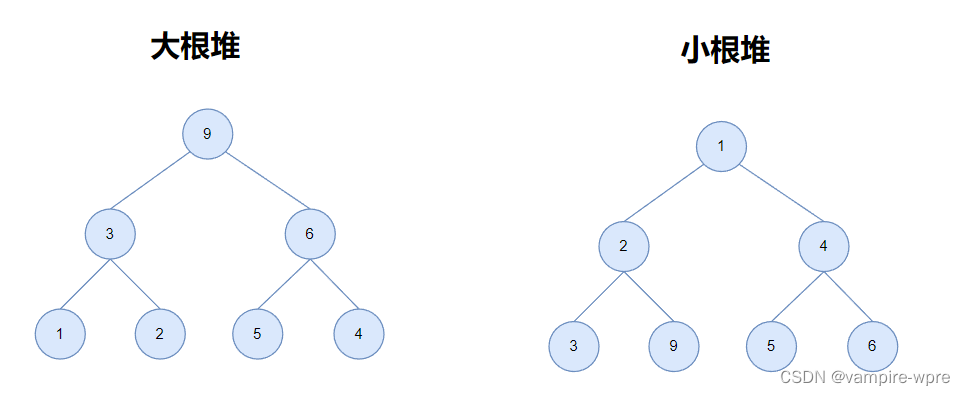
堆，可以认为是一棵使用顺序存储的方式来存储数据的一棵完全二叉树，堆分为大根堆和小根堆
大根堆：每个结点的值都不小于左右孩子结点的值
小根堆：每个结点的值都不大于左右孩子结点的值
如图：
在这里插入图片描述

复习：
如果父亲结点是i下标：左孩子2i+1；右孩子2i+2
如果孩子结点是i下标：父亲（ i-1）/ 2（不管i是左孩子还是右孩子）

2. PriorityQueue的实现

PriorityQueue默认是小根堆，所以我们也实现一个小根堆，文章最后会给出大根堆和小根堆的全部代码哦

2.0 搭建整体框架

定义一个Heap类

public class Heap {
    public int[] elem;//存储数据的数组
    public int curSize;//当前数据的个数
}

2.1 堆的创建和调整

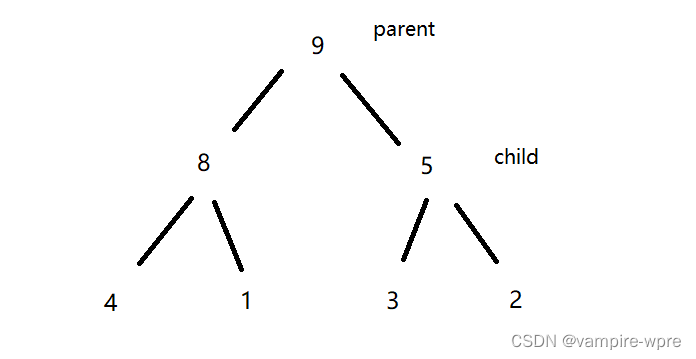
当拿到一组数据后如：2、4、3、9、6、1、5，如何将这组数据调整为小根堆？先将数据按层序遍历的方式，画出一棵二叉树，如图：

从最后一棵子树开始调整，循环直到整棵树都是小根堆

    //创建堆(小根堆)
    public void createHeap() {
        for (int parent = (elem.length - 1 - 1) / 2; parent >= 0; parent--) {
            shiftDown(elem, parent, elem.length);
        }
    }

    //向下调整的逻辑:
	private void shiftDown(int[] array, int parent, int end) {
        int child = (parent * 2) + 1;
        while (child < end) {
            if (child + 1 < end && array[child] > array[child + 1]) {
                child++;
            }
            //保证child下标是最小的
            if (array[child] < array[parent]) {
            	//交换child下标和parent下标的值
            	int tmp = array[child];
            	array[child] = array[parent];
            	array[parent] = tmp;
            	//
                parent = child;
                child = parent * 2 + 1;
            } else {
                break;//已经是小根堆了,结束循环
            }
        }
    }

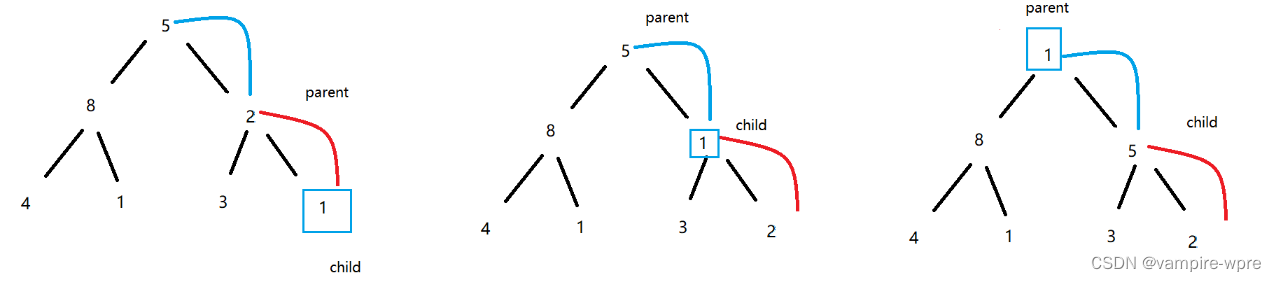
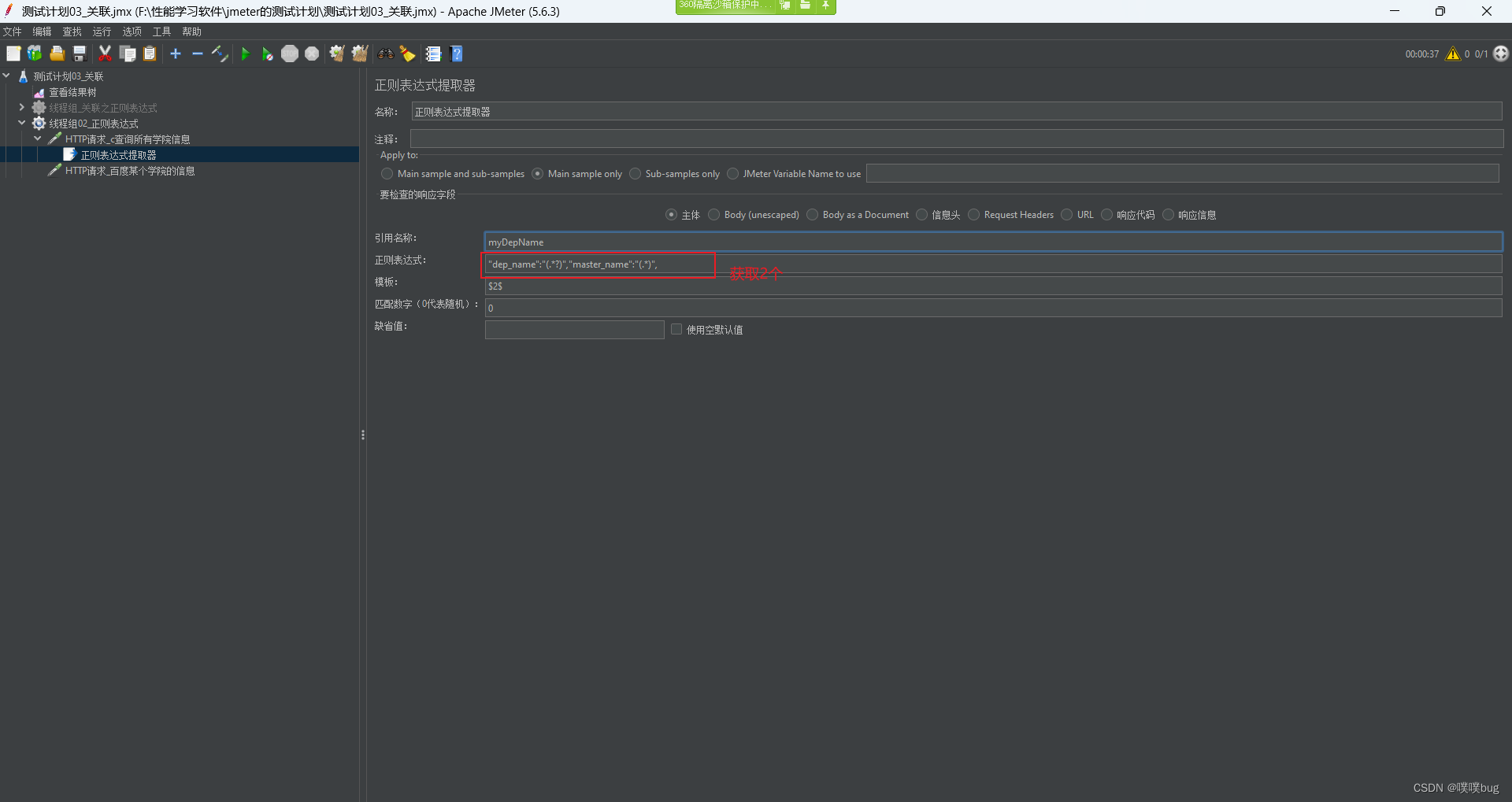
如何调整?拿parent=0举例
如图：调整
在这里插入图片描述
以下是进行一次调整的逻辑，对每棵子树都进行向下调整，整棵树就能变成小根堆
在这里插入图片描述

2.2 插入元素

插入是在数组的最后一个元素之后插入，插入之后的堆中的最后一个元素定义为child，child和它的父亲比较，将较小的做为根节点，接着
在这里插入图片描述

    public void offer(int key) {
        if (curSize == elem.length) {
            //扩容
            elem = Arrays.copyOf(elem, elem.length * 2);
        }
        elem[curSize] = key;
        curSize++;
        shiftUp(curSize - 1);
    }

//向上调整
    public void shiftUp(int child) {
        int parent = (child - 1) / 2;
        while (parent >= 0) {
            if (elem[child] > elem[parent]) {
            	//交换
            	int tmp = elem[child];
            	elem[child] = elem[parent];
            	elem[parent] = tmp;
            	
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

2.3 出堆顶元素

将堆顶元素和最后一个元素交换，前有效数据个数-1，接着将删除后的堆进行向上调整

    public int pool() {
        int ret = elem[0];
        swap(elem, 0, curSize - 1);
        curSize--;
        shiftDown(elem, 0, curSize);
        return ret;
    }

3. 全部代码（包含大根堆和小根堆）

public class Heap {

    public int[] elem;//存储数据的数组
    public int curSize;//当前数据的个数

    public Heap(int[] array) {
        //构造方法,初始化时给elem数组
        elem = new int[10];
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            curSize++;
        }
    }
    //创建堆(大根堆)
    public void createMaxHeap(int[] array) {
        for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {
            shiftDownMax(elem, parent, array.length);
        }
    }

    //创建堆(小根堆)
    public void createMinHeap(int[] array) {
        for (int parent = (elem.length - 1 - 1) / 2; parent >= 0; parent--) {
            shiftDownMin(elem, parent, elem.length);
        }
    }

    //向下调整:大根堆
    private void shiftDownMax(int[] array, int parent, int end) {
        int child = (parent * 2) + 1;

        while (child < end) {
            if (child + 1 < end && array[child] < array[child + 1]) {
                child++;
            }
            //child是最大的
            if (array[child] > array[parent]) {
                swap(array, child, parent);
                parent = child;
                child = parent * 2 + 1;
            } else {
                break;//已经是大根堆了,结束循环
            }
        }
    }

    //向下调整:小根堆
    private void shiftDownMin(int[] array, int parent, int end) {
        int child = (parent * 2) + 1;

        while (child < end) {
            if (child + 1 < end && array[child] > array[child + 1]) {
                child++;
            }
            //child是最大的

            if (array[child] < array[parent]) {
                swap(array, child, parent);
                parent = child;
                child = parent * 2 + 1;
            } else {
                break;//已经是小根堆了,结束循环
            }
        }
    }

    /**
     * 插入数据,大根堆
     *
     * @param key
     */
    public void offerMax(int key) {
        if (curSize == elem.length) {
            //扩容
            elem = Arrays.copyOf(elem, elem.length * 2);
        }
        elem[curSize] = key;
        curSize++;
        shiftUpMax(curSize - 1);
    }

    /**
     * 插入数据,小根堆
     *
     * @param key
     */
    public void offerMin(int key) {
        if (curSize == elem.length) {
            //扩容
            elem = Arrays.copyOf(elem, elem.length * 2);
        }
        elem[curSize] = key;
        curSize++;
        shiftUpMin(curSize - 1);
    }

    /**
     * 删除数据,大根堆
     *
     * @return
     */
    public int poolMax() {
        if (isEmpty()) {
            return -1;
        }
        int ret = elem[0];
        swap(elem, 0, curSize - 1);
        curSize--;
        shiftDownMax(elem, 0, curSize);
        return ret;
    }

    /**
     * 删除数据,小根堆
     * @return
     */
    public int poolMin() {
        if (isEmpty()) {
            return -1;
        }
        int ret = elem[0];
        swap(elem, 0, curSize - 1);
        curSize--;
        shiftDownMin(elem, 0, curSize);
        return ret;
    }

    //向上调整,大顶堆
    private void shiftUpMax(int child) {
        int parent = (child - 1) / 2;
        while (parent >= 0) {
            if (elem[child] > elem[parent]) {
                swap(elem, parent, child);
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    //向上调整,大顶堆
    private void shiftUpMin(int child) {
        int parent = (child - 1) / 2;
        while (parent >= 0) {
            if (elem[child] < elem[parent]) {
                swap(elem, parent, child);
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    //交换
    private void swap(int[] arr, int x, int y) {
        int tmp = arr[x];
        arr[x] = arr[y];
        arr[y] = tmp;
    }

    @Override
    public String toString() {
        StringBuilder str = new StringBuilder();
        for (int i = 0; i < curSize; i++) {
            str.append(elem[i]);
            if (i != curSize - 1) {
                str.append(", ");
            }
        }
        return str.toString();
    }

    //判断是否为空
    private boolean isEmpty() {
        return curSize == 0;
    }
}

4. PriorityQueue的使用

PriorityQueue的插入、删除的方法名和我们实现的一样这里不多赘述，Java中的PriorityQueue默认是小根堆，如果想变成大根堆，需要在实例化时传入自己实现的比较器

class Com implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2 - o1;//大堆
    }
}
public static void main(String[] args) {
	PriorityQueue<Integer> queue = new PriorityQueue<>(new Com());
	queue.offer(1);
}

今天的内容就到这里~感谢大家的支持！

5. Top-K问题

Top-K问题是求一个数据集合中，前K个最大值或者最小值，例如班级排名前十、世界五百强等。我们很容易想到将数据进行排序，但是当数据量比较大时，排序的效率很低，而且并不能将数据全部加载到内存中，那么怎么解决这个问题？最好的办法就是使用堆。
求前K个最大的元素： 建一个大小为K的小堆，剩下的N-K个元素与堆顶比较，将不符合要求的元素替换掉
求前K个最小的元素： 建一个大小为K的大堆，剩下的N-K个元素与堆顶比较，将不符合要求的元素替换掉
例题：最小K个数

class intCmp implements Comparator<Integer> {

    @Override
    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1);
    }
}

class Solution {
    public int[] smallestK(int[] arr, int k) {
        PriorityQueue<Integer> queue = new PriorityQueue<>(new intCmp());
        int[] ret = new int[k];// 要返回的数组
        if (k == 0) {
            return ret;
        }
        // 建大小为k的大根堆
        for (int i = 0; i < k; i++) {
            queue.offer(arr[i]);
        }
        for (int i = k; i < arr.length; i++) {
            int val = queue.peek();
            if (val > arr[i]) {
                queue.poll();
                queue.offer(arr[i]);
            }
        }

        for (int i = 0; i < k; i++) {
            ret[i] = queue.poll();
        }
        return ret;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1610956.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

VLOOKUP函数使用，为什么会报错“引用有问题”?

VLOOKUP函数使用，为什么会报错“引用有问题”?

VLOOKUP函数的使用非常广泛&#xff0c;在excel2007版之后的软件中&#xff0c;使用VLOOKUP函数也许会遇到这样的场景&#xff0c;明明公式是没有问题的&#xff0c;公式还会报错“引用有问题”。 一、报错场景 输入公式后&#xff0c;回车确认&#xff0c;显示如下报错&…
阅读更多...
嵌入式学习57-ARM7(字符设备驱动框架led)

嵌入式学习57-ARM7(字符设备驱动框架led)

知识零碎&#xff1a; kernel 内核 printk 内核打印 cat /proc/devices mknod ? 查看指令 gcc -oapp hello.c 字符设备驱动流程 字符设备程序运行流程 gcc中-c和-o是编译时可选的参数 -c …
阅读更多...
揭阳硕榕超市管理系统的设计与实现(论文)_kaic

揭阳硕榕超市管理系统的设计与实现(论文)_kaic

摘 要 在互联网高速发展环境下&#xff0c;传统的管理手段无法满足对信息的高效、快速的管理要求。为顺应时代发展的需要&#xff0c;提高超市的管理效能&#xff0c;提高超市的管理速度&#xff0c;构建一个信息化的工作流程&#xff0c;揭阳硕榕超市管理系统应运而生。 根…
阅读更多...
Jmeter04：关联

Jmeter04：关联

1 Jmeter组件&#xff1a;关联 概括&#xff1a;2个请求之间不是独立的&#xff0c;一个请求响应的结果是作为另一个请求提交的数据&#xff0c;存在数据交互 1.1 是什么&#xff1f; 就是一个请求的结果是另一个请求提交的数据&#xff0c;二者不再是独立 1.2 为什么&#x…
阅读更多...
Python 面向对象——1.基本概念

Python 面向对象——1.基本概念

本章学习链接如下&#xff1a; 基本概念与语法 类&#xff08;Class&#xff09;&#xff1a;定义了一组对象共有的属性和方法的蓝图。类是创建对象的模板。 对象&#xff08;Object&#xff09;&#xff1a;类的实例。对象包含实际的数据和操作数据的方法。 属性&#xff0…
阅读更多...
7.MMD 法线贴图的设置与调教

7.MMD 法线贴图的设置与调教

前期准备 人物 导入温迪模型导入ray.x和ray_controler.pmx导入天空盒time of day调成模型绘制顺序&#xff0c;将天空盒调到最上方给温迪模型添加main.fx材质在自发光一栏&#xff0c;给天空盒添加time of lighting材质 打开材质里的衣服&#xff0c;发现只有一个衣服文件 …
阅读更多...
【Canvas与艺术】绘制黑白山间野营Camping徽章

【Canvas与艺术】绘制黑白山间野营Camping徽章

【说明】 中间的山月图是借用的网上的成图&#xff0c;不是用Canvas绘制的。 【成果图】 【代码】 <!DOCTYPE html> <html lang"utf-8"> <meta http-equiv"Content-Type" content"text/html; charsetutf-8"/> <head>…
阅读更多...
微信域名防封/QQ域名防封/域名状态检测/域名防红防封API平台源码

微信域名防封/QQ域名防封/域名状态检测/域名防红防封API平台源码

下载地址&#xff1a;API平台源码 这套源码是使用thinkphp3.1.3开发的&#xff0c;可以在PHP5.3-5.6下运行&#xff0c;程序是有一点老了&#xff0c;但是思路仍在&#xff01;然后&#xff0c;这套源码我已经成功搭建起来了&#xff0c;后台、个人&#xff08;用户&#xff0…
阅读更多...
跟TED演讲学英文：How AI could save (not destroy) education by Sal Khan

跟TED演讲学英文：How AI could save (not destroy) education by Sal Khan

How AI could save (not destroy) education Link: How AI could save (not destroy) education Speaker: Sal Khan Date: April 2023 文章目录 How AI could save (not destroy) educationIntroductionVocabularyTranscriptSummary后记 Introduction Sal Khan, the founder…
阅读更多...
【UE5 C++】VS2022下载安装

【UE5 C++】VS2022下载安装

先看一下UE和VS的兼容性 &#xff08;虚幻5&#xff1a;为虚幻引擎C项目设置Visual Studio开发环境&#xff09; &#xff08;虚幻4&#xff1a;设置虚幻引擎的Visual Studio&#xff09; 为了让VS更好兼容UE5&#xff0c;因此这里下载VS2022版本 步骤 1. 进入Visual Stud…
阅读更多...
Linux 共享内存 及 利用管道实现简单协同

Linux 共享内存 及 利用管道实现简单协同

共享内存&#xff08;Shared Memory&#xff09;是一种多个进程之间共享某些内存区域以进行通信的机制。这些共享的内存区域可以被多个进程访问&#xff0c;从而实现对进程间数据的快速交换。共享内存是最快的IPC&#xff08;Inter-Process Communication&#xff0c;进程间通信…
阅读更多...
OpenHarmony其他工具类—leveldb [GN编译]

OpenHarmony其他工具类—leveldb [GN编译]

简介 leveldb是一种快速键值存储库&#xff0c;提供从字符串键到字符串值的有序映射。 下载安装 直接在OpenHarmony-SIG仓中搜索leveldb并下载。 使用说明 以OpenHarmony 3.1 Beta的rk3568版本为例 库代码存放路径&#xff1a;./third_party/leveldb 修改添加依赖的编译脚本…
阅读更多...
【嵌入式DIY实例】-指纹锁

【嵌入式DIY实例】-指纹锁

DIY指纹锁 文章目录 DIY指纹锁1、硬件准备1.1 R307指纹传感器模介绍2、硬件接线原理图3、代码实现在这个项目中，我们将使用 Arduino 构建一个指纹门锁安全系统。 该系统可用于我们的家庭、办公室等提供安全保障。 我们还可以用它来打开门，只需将手指放在门锁上即可。 安全是许…
阅读更多...
【双曲几何】圆盘上的三角形概念

【双曲几何】圆盘上的三角形概念

目录 一、说明二、对偶三角形概念2.1 反演关系2.2 对偶关系2.3 找出三角形的对偶三角形 三、正交三角形概念3.1 通过对偶三角形&#xff0c;找到垂心3.2 正交三角形的概念3.3 中心射影点的概念 四、后记 一、说明 本文对双曲空间的三角形进行分析&#xff0c;本篇首先给出&am…
阅读更多...
GRAF: Generative Radiance Fields for 3D-Aware Image Synthesis

GRAF: Generative Radiance Fields for 3D-Aware Image Synthesis

GRAF: Generative Radiance Fieldsfor 3D-Aware Image Synthesis&#xff08;基于产生辐射场的三维图像合成&#xff09; 思维导图&#xff1a;https://blog.csdn.net/weixin_53765004/article/details/137944206?csdn_share_tail%7B%22type%22%3A%22blog%22%2C%22rType%22%3…
阅读更多...
电商技术揭秘三十：知识产权保护浅析

电商技术揭秘三十：知识产权保护浅析

电商技术揭秘相关系列文章&#xff08;上&#xff09; 相关系列文章&#xff08;中&#xff09; 电商技术揭秘二十&#xff1a;能化供应链管理 电商技术揭秘二十一:智能仓储与物流优化(上) 电商技术揭秘二十二:智能仓储与物流优化(下) 电商技术揭秘二十三&#xff1a;智能…
阅读更多...
【深度学习】wandb模型训练可视化工具使用方法

【深度学习】wandb模型训练可视化工具使用方法

【深度学习】wandb模型训练可视化工具使用方法 wandb简介功能介绍登陆注册以及API keysproject和runsproject和runs的关系 wandb的配置实验跟踪版本管理Case可视化分析可视化自动调参&#xff08;wandb.sweep&#xff09;配置wandb.sweep1.配置 sweep_config2.初始化 sweep con…
阅读更多...
机器学习周报第35周SE-LSTM

机器学习周报第35周SE-LSTM

文章目录 week35 SE-LSTM摘要Abstract一、文献阅读1. 题目2. abstract3. 网络架构3.1 Savitsky-Golay 滤波器3.2 模型结构——SE-LSTM 4. 文献解读4.1 Introduction4.2 创新点4.3 实验过程4.3.1 训练参数4.3.2 数据集4.3.3 实验设置4.3.4 实验结果 5. python环境下基于scipy实现…
阅读更多...
【Godot4自学手册】第三十九节利用shader（着色器）给游戏添加一层雾气效果

【Godot4自学手册】第三十九节利用shader（着色器）给游戏添加一层雾气效果

今天&#xff0c;主要是利用shader给游戏给地宫场景添加一层雾气效果&#xff0c;增加一下气氛&#xff0c;先看一下效果&#xff1a; 一、新建ParallaxBackground根节点 新建场景&#xff0c;根节点选择ParallaxBackground&#xff0c;命名为Fog&#xff0c;然后将该场景保…
阅读更多...
Docker安装教程，什么系统都有

Docker安装教程，什么系统都有

下载Docker 如果你的系统是图形界面的&#xff0c;比如windows、mac、ubuntu等&#xff0c;到 Docker 官网下载 Docker Desktop。 官网链接: https://www.docker.com/products/docker-desktop/ 根据你的系统选择对应的安装包&#xff0c;然后下载&#xff0c;是不是特别简单&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023