一、对称性的几种情况

1、1个对称点/对称轴

此种情况，用整体换元法解题
参考：三角函数的整体换元法

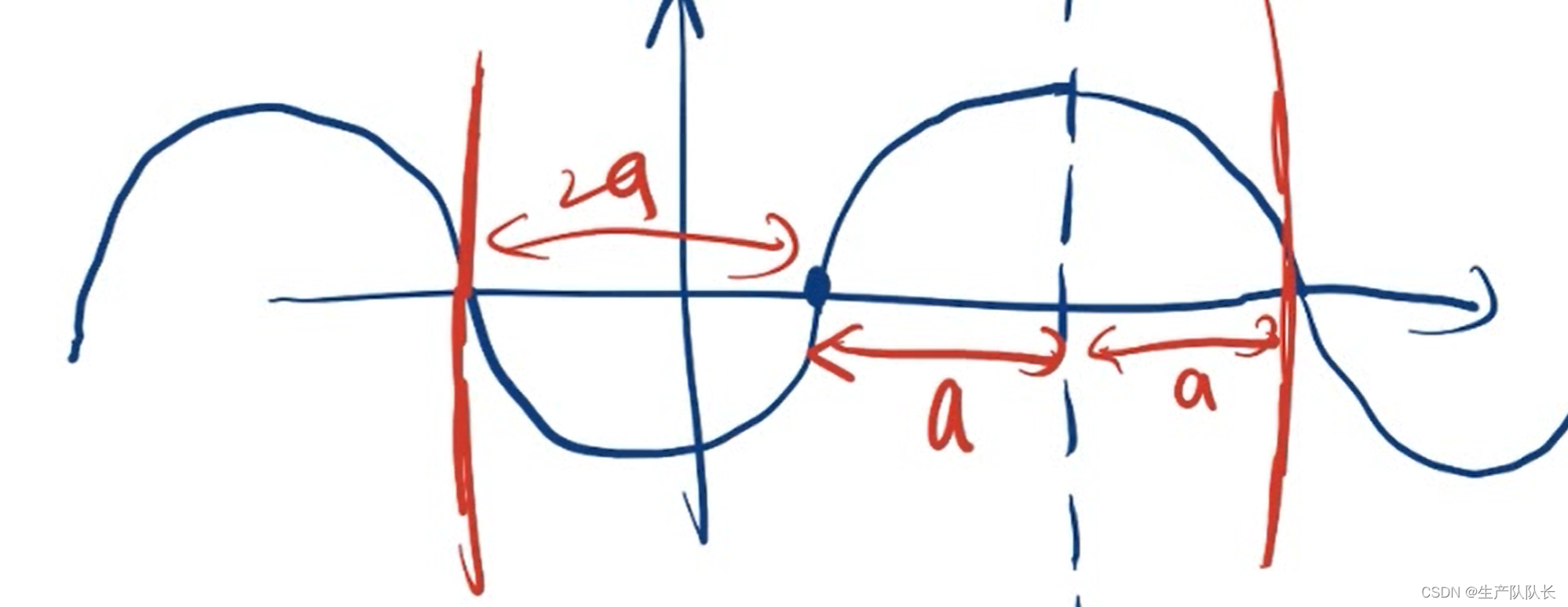
2、2个对称点

画图
如果两个对称点之间的距离是a，则函数周期T=2a

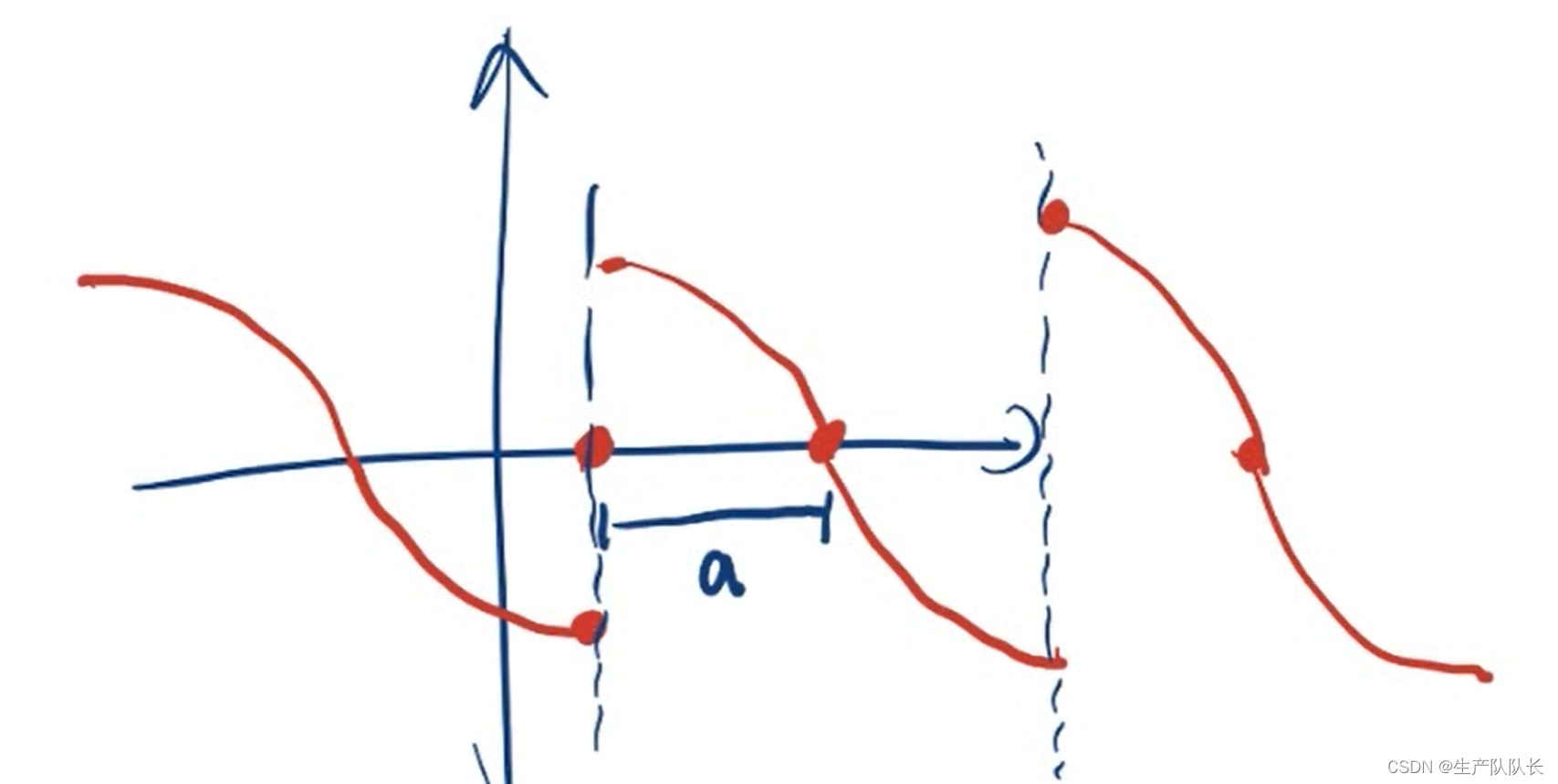
3、2个对称轴

画图
如果两个对称轴之间的距离是a，则函数周期T=2a

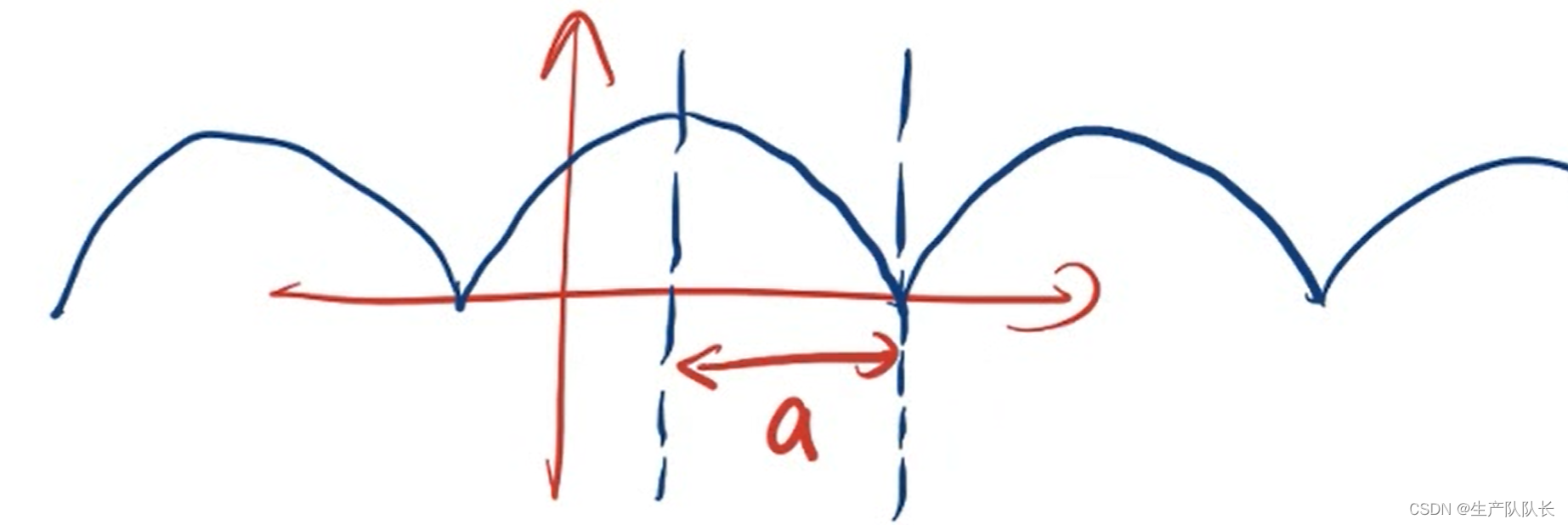
4、1个对称点和1个对称轴

画图
如果对称点和对称轴之间的距离是a，则函数周期T=4a

5、代数式表示法

对称轴（类似偶函数）

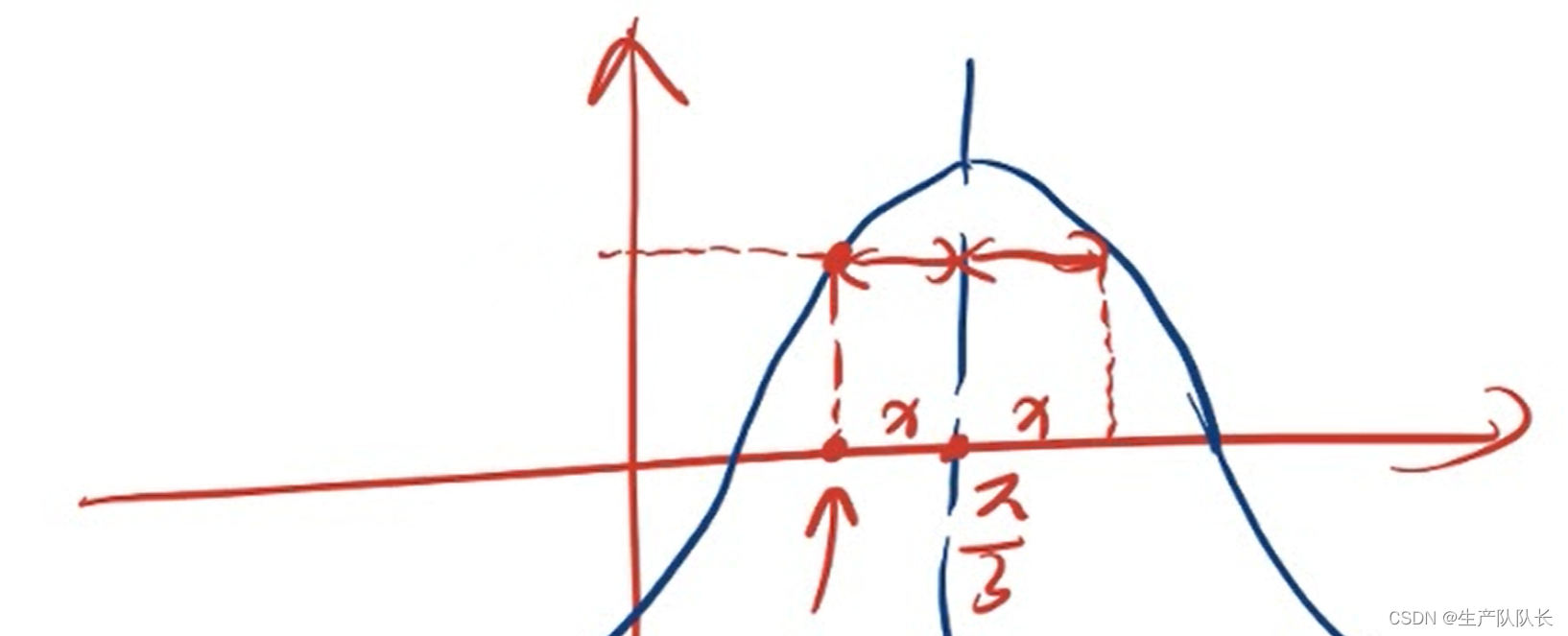
代数表达式

---

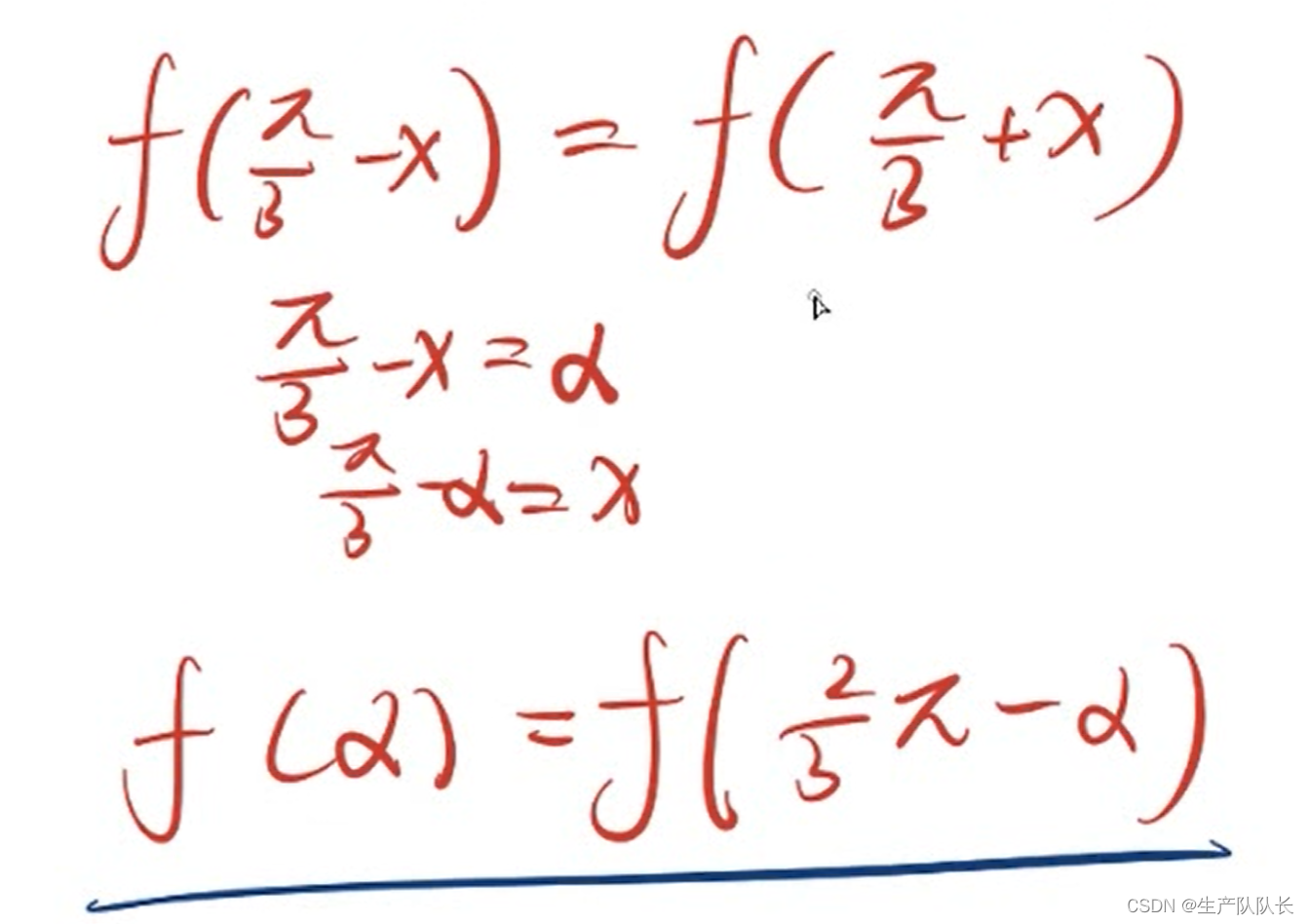
对称点（类似奇函数）

代数表达式

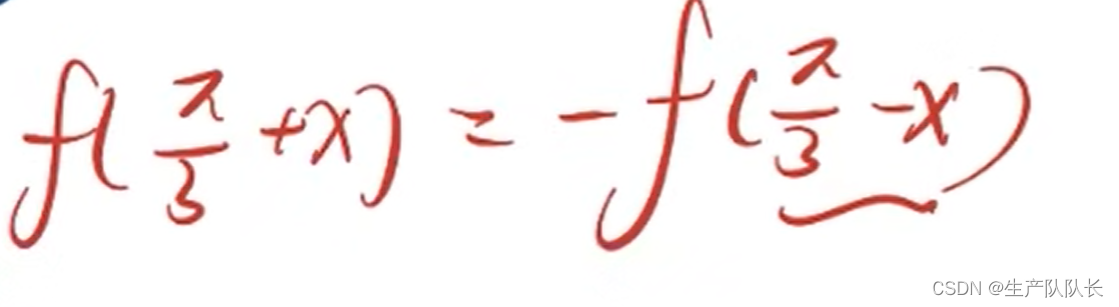
二、练习

例题1

补充条件ω>0

解析

这一题属于情况4，通过给出的条件，我们可以直接得出周期T和振幅A
在用整体换元法，求出相位φ，那么，函数f(x)的表达式就求出来了
然后，通过左加右减的平移规则，得出答案

---

例题2

解析

这一题，和例题1的解题过程差不多，先求出f(x)的表达式

选项A
首先，我们看到是cosx平移得到sinx，是异名函数间的平移问题，所以，自变量的值肯定相差π/2的倍数

选项B就不作解释，比较简单

选项C,D
我们要用整体换元法，把区间范围调整一下

且这两个选项，本质是复合函数问题，所以要记住口诀：同增异减
然后，可以通过画图解答，且离对称轴越远的点，则越大或者越小