牛客寒假集训营总结笔记——7道优质好题
一、Trie树的应用:
题目链接:Tokitsukaze and Min-Max XOR
1、题意

2、题解
1、首先这道题的答案和元素本身的顺序是无关的,因为假如你选择了一些数字,它是默认必须排好序才能记作是答案,所以对于我们枚举的任意一组max和min,位于 m i n ≤ x ≤ m a x min \le x \le max min≤x≤max的x是可取可不取的,所以就是 2 i − j − 1 + 1 2^{i-j-1}+1 2i−j−1+1就是当前位置作为max的贡献,怎么快速得到min呢,我们可以用01trie树得到。
2、01trie树详解(具体看代码):
首先是建树了,在每个节点的周围都放一个val节点存放该节点的儿子节点所有的
∑
(
2
−
i
)
\sum(2^{-i})
∑(2−i)。
然后就是搜索了,我们贪心的来使用trie树,当k在我们枚举的二进制位置为0时,当前二进制位必须和当前的max相抵消才能合法,当我们到达k的二进制为1的位置时,我们就可以直接把1^(max当前的二进制位)的贡献直接加上了,然后继续往下,类似于数位dp一样的思想去看。
3、代码
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 10;
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + 7;
int n,m,cnt;
int a[N];
int son[N*40][2], val[N*40];
int qpow(int x, int y) {
int res = 1;
while(y) {
if(y & 1) res = res * x % mod;
x = x * x % mod;
y >>= 1;
}
return res;
}
// 建树
void insert(int x, int nums) {
int p = 1;
for(int i = 35; i >= 0; -- i ) {
int t = x >> i & 1;
if(!son[p][t]) {
son[p][t] = ++ cnt;
int q = cnt;
son[q][1] = son[q][0] = 0;
val[q]=0;
}
p = son[p][t];
val[p] = (val[p]+nums)%mod;
}
}
//查询操作
int query(int x, int k) {
int res=0,p=1;
for(int i = 35; i >= 0; -- i ) {
int ps = k >> i & 1;
int cur = x >> i & 1;
if(ps) {
if(son[p][cur]) res = (res + val[son[p][cur]]) % mod;
p = son[p][1^cur];
}
else p = son[p][cur];
}
res = (res + val[p]) % mod;
return res;
}
void solve() {
cin >> n >> m;
cnt=1;
for(int i = 1; i <= n; ++ i ) cin >> a[i];
sort(a + 1, a + 1 + n);
val[cnt]=0;
son[cnt][0]=son[cnt][1]=0;
int ans=0;
for(int i = 1; i <= n; ++ i ) {
ans = (ans + 1 + qpow(2,i - 1) * query(a[i],m) % mod) % mod;
insert(a[i],qpow(qpow(2,i),mod-2));
}
cout<<ans<<endl;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T -- ) solve();
return 0;
}
二、朴素懒标记的应用和模板总结:
题目链接: Tokitsukaze and Power Battle (easy)
1、题意:

2、题解
数据范围已经告诉我们了,只会增加非负数并且原数组元素也都是非负数,因为要让差距尽可能的大,所以肯定要从左边一直选择并且另一个玩家选择右边的后一个,保证它是最小的,比如:给定了我们 l , r l,r l,r,那我们需要的方案肯定是 m a x ( s u m [ L . . R ] − a [ R + 1 ] ) max(sum[L..R] - a[R + 1]) max(sum[L..R]−a[R+1]),因为我们贪心可以知道必须选择第一个元素,那么其实我们只需要维护一个 s [ 1.... l ] − a [ l + 1 ] s[1....l] - a[l + 1] s[1....l]−a[l+1],加上懒标记即可,比如我们需要讲将 a x a_x ax改成 y y y,只需要维护区间加法即可,即区间 x . . . n x...n x...n加上 − a x + y {-a_x+y} −ax+y,与此同时我们再维护一个树状数组动态记录数组的前缀和,这样查询的时候我们就可以总结 q u e r y ( 1 , l , r ) − s u m ( l − 1 ) query(1,l,r)-sum(l-1) query(1,l,r)−sum(l−1)。
3、懒标记维护区间加法和区间最大值最小值:
#define int long long
using namespace std;
const int N = 5e5 + 10;
const int inf = 0x3f3f3f3f;
int n, m;
int a[N];
struct node
{
int l, r;
int mx,mn;
int lz;
}tr[N * 4];
void pushup(node &t, node& l, node& r)
{
t.mx = max(l.mx, r.mx);
t.mn = min(l.mn, r.mn);
}
void pushup(int u)
{
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void pushdown(int u)
{
if(!tr[u].lz) return;
node &l = tr[u << 1], &r = tr[u << 1 | 1];
l.mx = l.mx + tr[u].lz, l.lz += tr[u].lz;
r.mx = r.mx + tr[u].lz, r.lz += tr[u].lz;
l.mn = l.mn + tr[u].lz;
r.mn = r.mn + tr[u].lz;
tr[u].lz = 0;
pushup(u);
}
void build(int u, int l, int r)
{
tr[u].l = l, tr[u].r = r;
if(l == r)
{
tr[u].lz = 0;
tr[u].mx = a[l] - (a[l + 1] - a[l]);
tr[u].mn = a[l] - (a[l + 1] - a[l]);
}
else
{
tr[u].lz = 0;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void change(int u, int l, int r, int d)
{
node& t = tr[u];
if(t.l >= l && t.r <= r)
{
t.mx += d;
t.mn += d;
t.lz += d;
}
else
{
pushdown(u);
int mid = t.l + t.r >> 1;
if(l <= mid) change(u << 1, l, r, d);
if(r > mid) change(u << 1 | 1, l, r, d);
pushup(u);
}
}
int query_mx(int u, int l, int r)
{
node t = tr[u];
if(t.l >= l && t.r <= r) return t.mx;
else
{
pushdown(u);
int res = -1e18;
int mid = t.l + t.r >> 1;
if(l <= mid) res = max(res,query_mx(u << 1, l, r));
if(r > mid) res = max(res,query_mx(u << 1 | 1, l, r));
return res;
}
}
int query_mn(int u, int l, int r)
{
node t = tr[u];
if(t.l >= l && t.r <= r) return t.mn;
else
{
pushdown(u);
int res = 1e18;
int mid = t.l + t.r >> 1;
if(l <= mid) res = min(res,query_mn(u << 1, l, r));
if(r > mid) res = min(res,query_mn(u << 1 | 1, l, r));
return res;
}
}
4、代码:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#define int long long
using namespace std;
const int N = 5e5 + 10;
const int inf = 0x3f3f3f3f;
int n, m;
int a[N];
struct node
{
int l, r;
int mx,mn;
int lz;
}tr[N * 4];
void pushup(node &t, node& l, node& r)
{
t.mx = max(l.mx, r.mx);
t.mn = min(l.mn, r.mn);
}
void pushup(int u)
{
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void pushdown(int u)
{
if(!tr[u].lz) return;
node &l = tr[u << 1], &r = tr[u << 1 | 1];
l.mx = l.mx + tr[u].lz, l.lz += tr[u].lz;
r.mx = r.mx + tr[u].lz, r.lz += tr[u].lz;
l.mn = l.mn + tr[u].lz;
r.mn = r.mn + tr[u].lz;
tr[u].lz = 0;
pushup(u);
}
void build(int u, int l, int r)
{
tr[u].l = l, tr[u].r = r;
if(l == r)
{
tr[u].lz = 0;
tr[u].mx = a[l] - (a[l + 1] - a[l]);
tr[u].mn = a[l] - (a[l + 1] - a[l]);
}
else
{
tr[u].lz = 0;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void change(int u, int l, int r, int d)
{
node& t = tr[u];
if(t.l >= l && t.r <= r)
{
t.mx += d;
t.mn += d;
t.lz += d;
}
else
{
pushdown(u);
int mid = t.l + t.r >> 1;
if(l <= mid) change(u << 1, l, r, d);
if(r > mid) change(u << 1 | 1, l, r, d);
pushup(u);
}
}
int query_mx(int u, int l, int r)
{
node t = tr[u];
if(t.l >= l && t.r <= r) return t.mx;
else
{
pushdown(u);
int res = -1e18;
int mid = t.l + t.r >> 1;
if(l <= mid) res = max(res,query_mx(u << 1, l, r));
if(r > mid) res = max(res,query_mx(u << 1 | 1, l, r));
return res;
}
}
int query_mn(int u, int l, int r)
{
node t = tr[u];
if(t.l >= l && t.r <= r) return t.mn;
else
{
pushdown(u);
int res = 1e18;
int mid = t.l + t.r >> 1;
if(l <= mid) res = min(res,query_mn(u << 1, l, r));
if(r > mid) res = min(res,query_mn(u << 1 | 1, l, r));
return res;
}
}
int trr[N];
#define lowbit(x) (x&-x)
void add(int x, int c) {
for(int i = x; i <= n; i += lowbit(i)) trr[i] += c;
}
int sum(int x) {
int res = 0;
for(int i = x; i; i -= lowbit(i)) res += trr[i];
return res;
}
void solve() {
scanf("%lld%lld",&n,&m);
for(int i = 0; i <= n; ++ i ) trr[i] = 0;
for(int i = 1; i <= n; ++ i ) {
scanf("%lld",&a[i]);
add(i,a[i]);
a[i] += a[i - 1];
}
a[n + 1] = a[n];
build(1,1,n);
while(m -- ) {
int x, y, z;
cin >> x >> y >> z;
if(x == 1) {
int tt = sum(y) - sum(y-1);
add(y,z-tt);
change(1,y,n,z-tt);
if(y-1>=1) change(1,y-1,y-1,-(z-tt));
}
else {
cout<<query_mx(1,y,z-1)-sum(y-1)<<endl;
}
}
}
signed main()
{
int ts;
scanf("%lld",&ts);
while(ts -- ) solve();
return 0;
}
三、第二类斯特林数
题目链接:鸡数题
1、题意:

2、题解:
问题可以很容易的转换成将n个小球放到m个盒子的方案,并且每个盒子都要有小球,第二类斯特林数是一个组合数学中的概念,表示将 n n n 个不同的物体划分成 k k k 个非空的不可辨别的集合的方法数。
通项公式为:转自oi-wiki
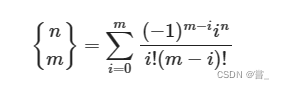
3、代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
int n, m;
int f1[N], f2[N];
int qmi(int x, int y) {
int res = 1;
while(y) {
if(y & 1) res = res * x % mod;
x = x * x % mod;
y >>= 1;
}
return res;
}
int f(int a, int b) {
return f1[a] * f2[a - b] % mod * f2[b] % mod;
}
signed main() {
cin >> n >> m;
if(n < m) {
cout << 0 << endl;
return 0;
}
if(n == m) {
cout << 1 << endl;
return 0;
}
f1[0] = 1, f2[0] = 1;
for(int i = 1; i <= n; ++ i ) {
f1[i] = (f1[i - 1] * i) % mod;
f2[i] = qmi(f1[i], mod - 2);
}
int ans = 0;
for(int i = 0; i <= m; ++ i )
ans = (ans + qmi(-1, i) * f(m, i) % mod * qmi(m - i, n) % mod) % mod;
ans = (ans * f2[m] % mod + mod) % mod;
cout<<ans<<endl;
return 0;
}
四、贡献题的新思路
题目链接:tomorin的字符串迷茫值
1、题意:

2、题解:
一般我们做这种贡献题都是想着每种方案对答案的贡献,这道题换了一种思考的角度,我们对每种情况内的每个子情况对子情况所在的所有情况的贡献,比如mygo,就会有mygo, m_ygo,m_y_go…,m和y,y和g,g和o之间的位置都可以选和不选,求每个位置如果有当前这种情况,两边任意删除的情况就是它对他所在方案内的贡献。
怎么计算两边的任意情况的贡献呢,这里就需要dp了,dp[i]定义为长度为i的字符串,不删除连续位置的所有方案数。那么我们只需要考虑最后一个位置的字符,它既可以删也可以不删,如果保留就是dp[i-1],,如果删除,那就是dp[i-2],因为i-1不能删除,然后就是 d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i] = dp[i-1]+dp[i-2] dp[i]=dp[i−1]+dp[i−2],就是斐波那契数列。
对于任意位置i…j的贡献计算就是: d p [ i − 1 ] ∗ d p [ n − i ] dp[i-1]*dp[n-i] dp[i−1]∗dp[n−i]
3、代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
int n,m,k;
int f[N];
int qpow(int x, int y) {
int res = 1;
while(y) {
if(y&1)res=res*x%mod;
x=x*x%mod;
y>>=1;
}
return res;
}
signed main() {
f[0]=1,f[1]=2;
for(int i = 2; i < N; ++ i ) f[i] = (f[i - 1] + f[i - 2]) % mod;
string s;
cin>>s;
n=s.size();
int ans=0;
for(int i = 0; i < 1<<3; ++ i ) {
string us="m";
if(i>>0&1)us+='1';
us+='y';
if(i>>1&1)us+='1';
us+='g';
if(i>>2&1)us+='1';
us+='o';
int le=us.size();
int t = 0;
for(int j = 0; j + le - 1 < n; ++ j ) {
string tmp = s.substr(j,le);
bool flag=1;
for(int k = 0; k < le; ++ k )
if(us[k]!=tmp[k]&&us[k]!='1') {
flag=0;
break;
}
if(flag) {
ans = (ans + f[j]*f[n-1-(j+le-1)]%mod)%mod;
}
}
}
cout<<ans<<endl;
return 0;
}
五、完全背包变形题
题目链接:soyorin的通知
完全背包板子:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1010 + 10;
int n,m;
int dp[N];
signed main() {
cin>>n>>m;
// memset(dp,-0x3f,sizeof dp);
dp[0]=0;
for(int i = 1; i <= n; ++ i ) {
int v,w;
cin>>v>>w;
for(int i = v; i <= m; ++ i )
dp[i]=max(dp[i],dp[i-v]+w);
}
cout<<dp[m]<<endl;
return 0;
}
1、题意

2、题解
因为刚开始必须要至少先用p的代价先通知一个人,才能进行完全背包,那我们不妨先进行完全背包,然后再枚举用了几次的p,但注意必须至少一次。
3、代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1010;
int n,m;
int dp[N];
int a[N],b[N];
signed main() {
cin>>n>>m;
for(int i = 1; i <= n; ++ i ) cin>>a[i]>>b[i];
memset(dp,0x3f,sizeof dp);
dp[0]=0;
for(int i = 1; i <= n; ++ i ) {
for(int j = 0; j <= n; ++ j )
dp[j]=min(dp[j],dp[max(0ll,j-b[i])]+a[i]);
}
int ans=1e18;
for(int i = 0; i < n; ++ i )
ans=min(ans,dp[i]+(n-i)*m);
// cout<<dp[n]<<endl;
cout<<ans<<endl;
return 0;
}
六、区间贪心问题 陡峭值问题
题目链接: rikki的数组陡峭值
1、题意

2、题解
首先假如我们有一堆的区间
[
l
1
,
r
1
]
,
[
l
2
,
r
2
]
,
.
.
.
,
[
l
n
,
r
n
]
[l_1,r_1],[l_2,r_2],...,[l_n,r_n]
[l1,r1],[l2,r2],...,[ln,rn], 此时我们假设有三个区间,
s
e
g
1
=
[
l
1
,
r
1
]
,
s
e
g
2
=
[
l
2
,
r
2
]
,
s
e
g
3
=
[
l
3
,
r
3
]
seg_1=[l_1,r_1],seg_2=[l_2,r_2],seg_3=[l_3,r_3]
seg1=[l1,r1],seg2=[l2,r2],seg3=[l3,r3]
对于
s
e
g
1
∩
s
e
g
3
=
∅
,
s
e
g
2
∩
s
e
g
3
≠
∅
,
s
e
g
2
∩
s
e
g
1
≠
∅
seg_1 \cap seg_3 = \empty, seg_2 \cap seg_3 \neq \empty, seg_2 \cap seg_1 \neq \empty
seg1∩seg3=∅,seg2∩seg3=∅,seg2∩seg1=∅,
s
e
g
2
seg_2
seg2 无论是和
s
e
g
1
seg_1
seg1或者是
s
e
g
3
seg_3
seg3合并, 结果一定
≥
a
b
s
(
s
e
g
3
.
l
−
s
e
g
1
.
r
)
\geq abs(seg_3.l-seg_1.r)
≥abs(seg3.l−seg1.r),所以我们肯定优先合并
s
e
g
1
seg_1
seg1,因为合并
s
e
g
3
seg_3
seg3会使得后面能合并的区间变少,肯定更劣。
其它情况,很显然是和能合并的区间合并。
3、代码
#include <bits/stdc++.h>
#define lowbit(x) (x&-x)
#define int long long
#define ff first
#define ss second
using namespace std;
using PII = pair<int, int>;
const int N = 3e5 + 10;
const int inf = 1e18;
int n, m, k;
int dp[N][2];
void solve() {
cin>>n;
int l=1,r=1e9;
vector<PII> ve;
for(int i = 1; i <= n; ++ i ) {
int L,R;
cin>>L>>R;
if(i==1) l=L,r=R;
else {
if(R<l||L>r) {
ve.push_back({l,r});
l=L,r=R;
}
else {
l=max(l,L),r=min(r,R);
// cout<<l<<' '<<r<<endl;
}
}
}
ve.push_back({l,r});
// for(int i = 0; i < ve.size(); ++ i ) cout<<ve[i].ff<<" "<<ve[i].ss<<endl;
if(ve.size()==1)cout<<0<<endl;
else {
for(int i = 1; i < ve.size(); ++ i ) {
dp[i+1][0]=min(dp[i][0]+abs(ve[i].ff-ve[i-1].ff),dp[i][1]+abs(ve[i].ff-ve[i-1].ss));
dp[i+1][1]=min(dp[i][0]+abs(ve[i].ss-ve[i-1].ff),dp[i][1]+abs(ve[i].ss-ve[i-1].ss));
}
cout<<min(dp[ve.size()][0],dp[ve.size()][1])<<endl;
}
}
signed main() {
int ts=1;
// cin >> ts;
while(ts -- ) solve();
return 0;
}
七、分部dp解决问题,将一个复杂难以解决的问题拆解。
题目链接:来点每日一题
1、题意

2、题解
一次性考虑所有的情况时间复杂度要做到 O ( n 3 ) O(n^3) O(n3),那肯定是超时了,我们不妨将问题转化成小的问题,先只考虑每段只选6个的方案,即 m x [ i ] [ j ] mx[i][j] mx[i][j],为i道j中选6个数的最优解,再做一遍线性dp,每次把一段看成一个整体, d p [ i ] = m a x ( d p [ i ] , d p [ j − 1 ] + m x [ j ] [ i ] ) dp[i] = max(dp[i], dp[j - 1] + mx[j][i]) dp[i]=max(dp[i],dp[j−1]+mx[j][i]),然后求mx[i][j]的过程也是一个很经典我问题,就是从i到j中选6个数使得它满足题目中的式子最大的方案,因为其中带有负号,所以我们得同时求最小值。
我们分部来看,首先是求 m x [ i ] [ j ] mx[i][j] mx[i][j]的过程:
for(int i = 1; i <= n; ++ i ) {
int f[7][3];
for(int j = 0; j <= 6; ++ j )
f[j][0]=-1e9,f[j][1]=1e9;
f[0][0]=f[0][1]=0;
for(int j = i; j <= n; ++ j ) {
for(int k = 6; k >= 1; -- k ) // 从后往前滚动数组,因为要利用上一个状态更新,不能从小到大,类似降维背包的写法。
for(int t = 0; t <= 1; ++ t)
{
if(abs(f[k-1][t])==1e9)continue; //到不合法不存在的方案要跳过,因为有负号可能会直接更新。
if(k % 2 == 0) {
f[k][0]=max(f[k][0],f[k-1][t]-a[j]);
f[k][1]=min(f[k][1],f[k-1][t]-a[j]);
}
else if(k == 1) {
f[k][0]=max(f[k][0],f[k-1][t]+a[j]);
f[k][1]=min(f[k][1],f[k-1][t]+a[j]);
}
else {
f[k][0]=max(f[k][0],f[k-1][t]*a[j]);
f[k][1]=min(f[k][1],f[k-1][t]*a[j]);
}
}
mx[i][j]=max(mx[i][j], f[6][0]);
}
}
有了 m x [ i ] [ j ] mx[i][j] mx[i][j]一切就很简单了
3、代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1010;
const int inf = 0x3f3f3f3f;
int n,m;
int a[N];
int dp[N],mx[N][N];
signed main() {
cin>>n;
for(int i = 1; i <= n; ++ i ) cin>>a[i];
for(int i = 1; i <= n; ++ i ) {
int f[7][3];
for(int j = 0; j <= 6; ++ j )
f[j][0]=-1e9,f[j][1]=1e9;
f[0][0]=f[0][1]=0;
for(int j = i; j <= n; ++ j ) {
for(int k = 6; k >= 1; -- k )
for(int t = 0; t <= 1; ++ t)
{
if(abs(f[k-1][t])==1e9)continue;
if(k % 2 == 0) {
f[k][0]=max(f[k][0],f[k-1][t]-a[j]);
f[k][1]=min(f[k][1],f[k-1][t]-a[j]);
}
else if(k == 1) {
f[k][0]=max(f[k][0],f[k-1][t]+a[j]);
f[k][1]=min(f[k][1],f[k-1][t]+a[j]);
}
else {
f[k][0]=max(f[k][0],f[k-1][t]*a[j]);
f[k][1]=min(f[k][1],f[k-1][t]*a[j]);
}
}
mx[i][j]=max(mx[i][j], f[6][0]);
}
}
int ans=0;
for(int i = 1; i <= n; ++ i ) {
dp[i]=dp[i-1];
for(int j = 1; j <= i; ++ j )
dp[i] = max(dp[i], dp[j-1]+mx[j][i]),ans=max(ans,dp[i]);
}
cout<<ans<<endl;
return 0;
}