LeetCode第22题：生成括号【22/1000 python 递归|动态规划】

news2024/10/7 8:27:16

作者介绍：10年大厂数据\经营分析经验，现任大厂数据部门负责人。
会一些的技术：数据分析、算法、SQL、大数据相关、python

欢迎加入社区：码上找工作http://t.csdnimg.cn/Q59WX作者专栏每日更新：
LeetCode解锁1000题: 打怪升级之旅

LeetCode解锁1000题: 打怪升级之旅https://blog.csdn.net/cciehl/category_12625714.html
python数据分析可视化：企业实战案例https://blog.csdn.net/cciehl/category_12615648.html
备注说明：方便大家阅读，统一使用python，带必要注释，公众号数据分析螺丝钉一起打怪升级

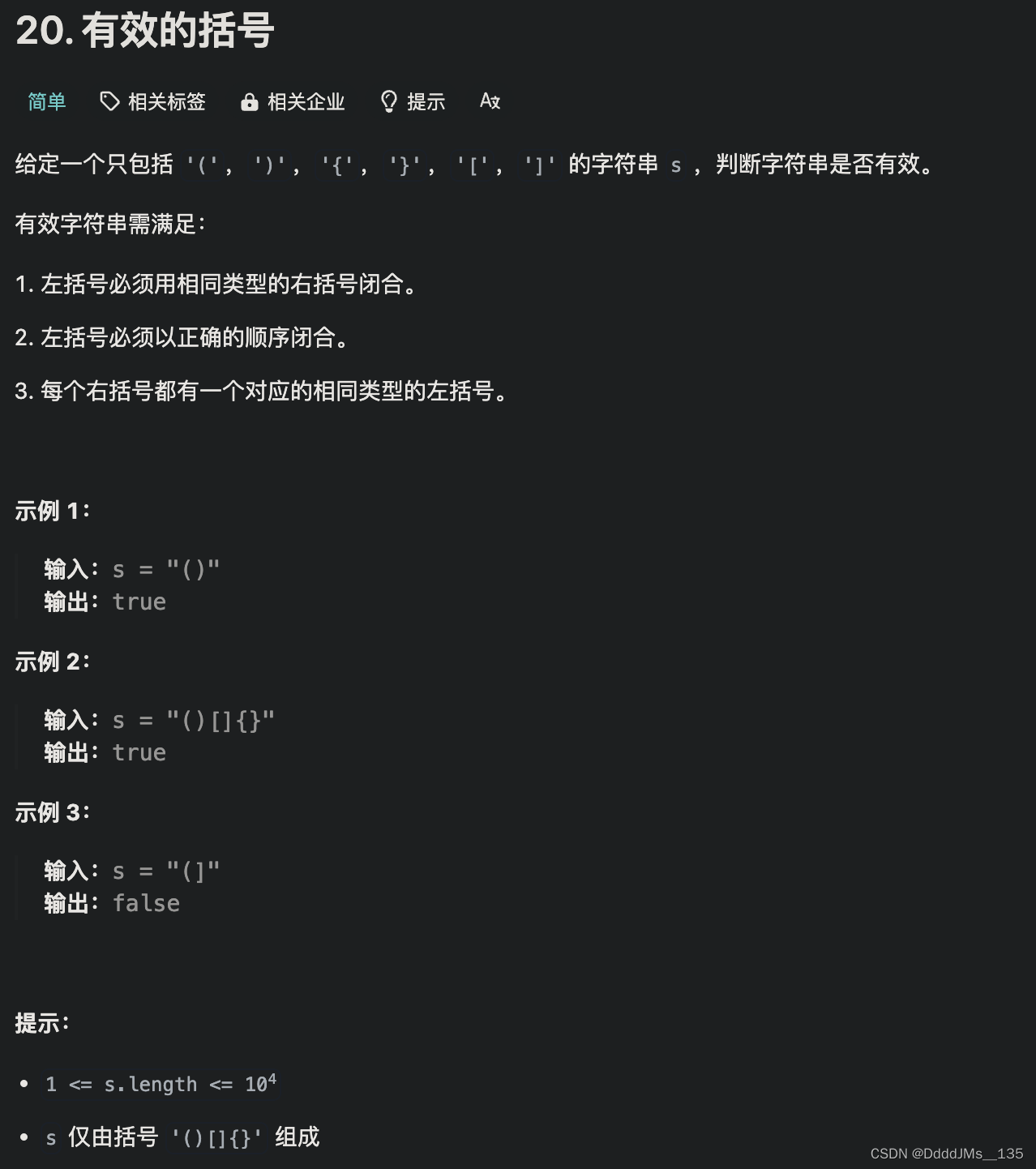
问题描述

给定一个数字 n，要求生成所有可能的并且有效的括号组合。

有效的括号组合需要满足以下条件：

左括号必须以正确的顺序闭合。
左括号和右括号的数量相等。

例如，当 n = 3 时，一个可能的解集为：

[  "((()))",  "(()())",  "(())()",  "()(())",  "()()()"]

解题思路

方法一：递归

解题步骤

要生成所有有效的括号组合，我们可以使用递归来逐步构建字符串。我们维护两个变量：左括号和右括号的剩余数量。在每一步中，我们都有两个选择：

如果左括号的数量不为0，我们可以添加一个左括号。
如果右括号的数量大于左括号的数量，我们可以添加一个右括号。

python示例

主函数 generateParenthesis：
- 输入参数 n 代表一对括号的数量。
- 定义了一个内部的辅助函数 backtrack，用于递归构建有效的括号组合。
- 定义一个列表 results，用来存储所有有效的括号组合。
- 最后，调用 backtrack 函数并返回 results。
辅助函数 backtrack：
- 接收三个参数：当前累积的括号字符串 accumulated，当前开括号的数量 open_brackets，和当前闭括号的数量 close_brackets。
- 递归的基准情况是当累积的字符串长度达到2n时，此时我们找到了一个有效的括号组合，将其添加到结果列表中。
- 如果开括号的数量小于n，我们可以添加一个开括号并递归地调用 backtrack。
- 如果闭括号的数量小于开括号的数量，这意味着我们可以添加一个闭括号而不破坏括号的有效性，因此我们再次递归地调用 backtrack，添加一个闭括号。

下面是一个Python示例代码

from typing import List

def generateParenthesis(n: int) -> List[str]:
    def backtrack(accumulated: str, open_brackets: int, close_brackets: int):
        # 当累积的字符串长度达到2n时，表示形成了一个有效的组合
        if len(accumulated) == 2 * n:
            results.append(accumulated)
            return
        # 如果开括号的数量少于n，可以添加一个开括号
        if open_brackets < n:
            backtrack(accumulated + '(', open_brackets + 1, close_brackets)
        # 如果闭括号数量少于开括号，可以添加一个闭括号
        if close_brackets < open_brackets:
            backtrack(accumulated + ')', open_brackets, close_brackets + 1)

    results = []
    backtrack('', 0, 0)
    return results

算法分析

时间复杂度：O(4^n / sqrt(n))，这是基于卡塔兰数的通项公式。
空间复杂度：O(n)，递归栈的空间。

方法二：动态规划

动态规划是解决这类问题的另一种有效方法，其基本思想是将问题分解为一系列相关的子问题，并存储这些子问题的解，以避免重复计算。

解题步骤

定义一个列表 dp 来存储所有解，其中 dp[i] 包含了所有由 i 对括号能组成的有效组合。
初始化 dp[0] = [""]，即没有括号时认为存在一个空的解。
对于每个 i 从 1 到 n（含），计算 dp[i] 的值：
- 遍历 j 从 0 到 i-1（含），我们将 dp[i] 的解视为在 dp[j] 的解的基础上添加一对括号，然后在里面填充 dp[i-j-1] 的解。
- 具体地，对于 dp[j] 中的每个字符串，我们在其外部添加一对括号，然后在这对括号内部尝试插入 dp[i-j-1] 中的所有可能的字符串。

python示例

def generateParenthesis(n: int) -> List[str]:
    dp = [[] for _ in range(n + 1)]
    dp[0] = [""]  # 初始化基础情况
    for i in range(1, n + 1):
        for j in range(i):
            for a in dp[j]:
                for b in dp[i-j-1]:
                    dp[i].append("(" + a + ")" + b)
    return dp[n]