给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

 graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

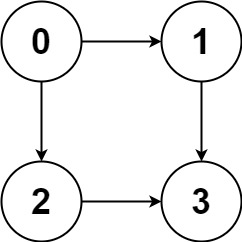
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

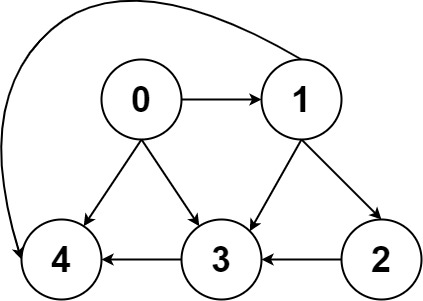
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i（即不存在自环）
• graph[i] 中的所有元素 互不相同
• 保证输入为 有向无环图（DAG）

    static List<List<Integer>> ans = new ArrayList<>();
    static List<Integer> cnt = new ArrayList<>();

    public static void dfs(int[][] graph, int node) {
        // 递归终止条件，如果当前结点等于最后一个结点说明到达终点
        if (node == graph.length - 1) {
            ans.add(new ArrayList<>(cnt));
            // 结束本次收集结果
            return;
        }

        for (int i = 0; i < graph[node].length; i++) {
            // 将当前结点保存至cnt中
            int nodeNode = graph[node][i];
            // 添加到收集路径中
            cnt.add(nodeNode);
            // 寻找下一个周围结点
            dfs(graph, nodeNode);
            // 回溯
            cnt.remove(cnt.size() - 1);
        }
    }


    public static List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        // 默认是从0开始的,所以需要把0加入结果集
        cnt.add(0);
        // 默认也是从0开始遍历的
        dfs(graph, 0);
        return ans;
    }

    public static void main(String[] args) {
        int[][] arr = new int[][]{{1, 2}, {3}, {3}, {}};
        allPathsSourceTarget(arr);
    }