一、AI 讲解
图论是数学的一个分支,主要研究图的性质。在图论中,最短路径问题是一个经典问题,它旨在找到图中两个顶点之间的最短路径长度。这个问题在很多实际应用中都非常重要,比如在网络路由、社交网络分析、城市交通规划等领域。
最短路径可以使用多种算法来计算,其中最著名的有:
-
Dijkstra算法:适用于带权有向图和无向图,可以找到一个顶点到图中所有其他顶点的最短路径。它的基本思想是每次找到离源点最近的一个顶点,然后以这个顶点为中间点,更新源点到其他所有顶点的距离。
-
Bellman-Ford算法:适用于含有负权边的图。这个算法可以检测图中是否存在负权回路,同时找到从单一源点出发到所有其他顶点的最短路径。
-
Floyd-Warshall算法:适用于计算所有顶点对之间的最短路径。该算法以动态规划的思想,逐渐扩展路径长度,最终得到任意两点之间的最短路径。
举个例子,假设你在一个城市的地图上,想要找到从家到办公室的最短路线。这个城市的地图可以被抽象为一个图,其中的顶点表示交叉路口,边表示道路,边的权重可以是距离、时间或者其他代价。使用最短路径算法,就可以计算出最快或距离最短的路线。
二、AI 出题
(1)题目
-
Dijkstra算法适用于以下哪种图?
A. 只有正权边的图
B. 只有负权边的图
C. 既有正权边也有负权边的图
D. 无权图 -
下列关于Bellman-Ford算法的描述中,哪一项是错误的?
A. 能够处理带有负权边的图
B. 无法检测图中的负权回路
C. 适用于有向图和无向图
D. 可以找到从单一源点出发到所有其他顶点的最短路径 -
Floyd-Warshall算法用于解决什么问题?
A. 单源最短路径问题
B. 所有顶点对的最短路径问题
C. 最小生成树问题
D. 最大流问题 -
在使用Dijkstra算法计算最短路径时,若引入了一个新的顶点Q,该顶点与图中某顶点P的距离为最短,那么下一步操作是什么?
A. 更新所有顶点到P的距离
B. 更新所有顶点到Q的距离
C. 仅更新P到源点的距离
D. 仅更新Q到源点的距离 -
如果一个图包含负权回路,那么下列哪个算法能正确处理并报告这一情况?
A. Dijkstra算法
B. Bellman-Ford算法
C. Floyd-Warshall算法
D. Prim算法 -
Dijkstra算法的时间复杂度是什么?
A. O(V^2)
B. O(V+E)
C. O(V*logV)
D. O(V^2 + E) -
Bellman-Ford算法的特点是什么?
A. 高效处理大规模图
B. 不能处理负权边
C. 可以检测负权回路
D. 只适用于无向图 -
Floyd-Warshall算法的时间复杂度是?
A. O(V^2)
B. O(V^3)
C. O(VE)
D. O(V^2*logV) -
在使用Dijkstra算法时,如果图中存在负权边,会出现什么问题?
A. 算法将更加高效
B. 算法无法保证找到最短路径
C. 算法的时间复杂度会降低
D. 不会对算法产生任何影响 -
使用Floyd-Warshall算法处理的图中,如果两个顶点之间不存在路径,则这两个顶点之间的最短路径长度是多少?
A. 0
B. 无穷大
C. 负无穷大
D. 1
(2)答案和解析
- 答案:A。Dijkstra算法只适用于只有正权边的图,因为它是基于贪心算法来寻找最短路径的,不能正确处理负权边。
- 答案:B。Bellman-Ford算法的一个重要特性就是能够检测图中是否存在负权回路。
- 答案:B。Floyd-Warshall算法用于解决所有顶点对的最短路径问题,可以计算图中任意两点间的最短路径长度。
- 答案:B。在Dijkstra算法中,引入新顶点Q后,会更新从源点到所有顶点(包括Q)的最短距离。
- 答案:B。Bellman-Ford算法能
够正确处理含有负权边的图,并能报告图中是否存在负权回路。
6. 答案:A。Dijkstra算法的时间复杂度为O(V^2),但如果使用优先队列优化,复杂度可以降低到O(V+logV)。
7. 答案:C。Bellman-Ford算法的一个显著特点是它可以处理负权边的图,并且能够检测出负权回路。
8. 答案:B。Floyd-Warshall算法的时间复杂度是O(V^3),这使得它适用于节点数量不是很大的图。
9. 答案:B。如果图中存在负权边,使用Dijkstra算法无法保证找到最短路径,因为Dijkstra算法假设所有边的权重都是非负的。
10. 答案:B。在Floyd-Warshall算法中,如果两个顶点之间不存在路径,它们之间的最短路径长度被定义为无穷大。
三、真题
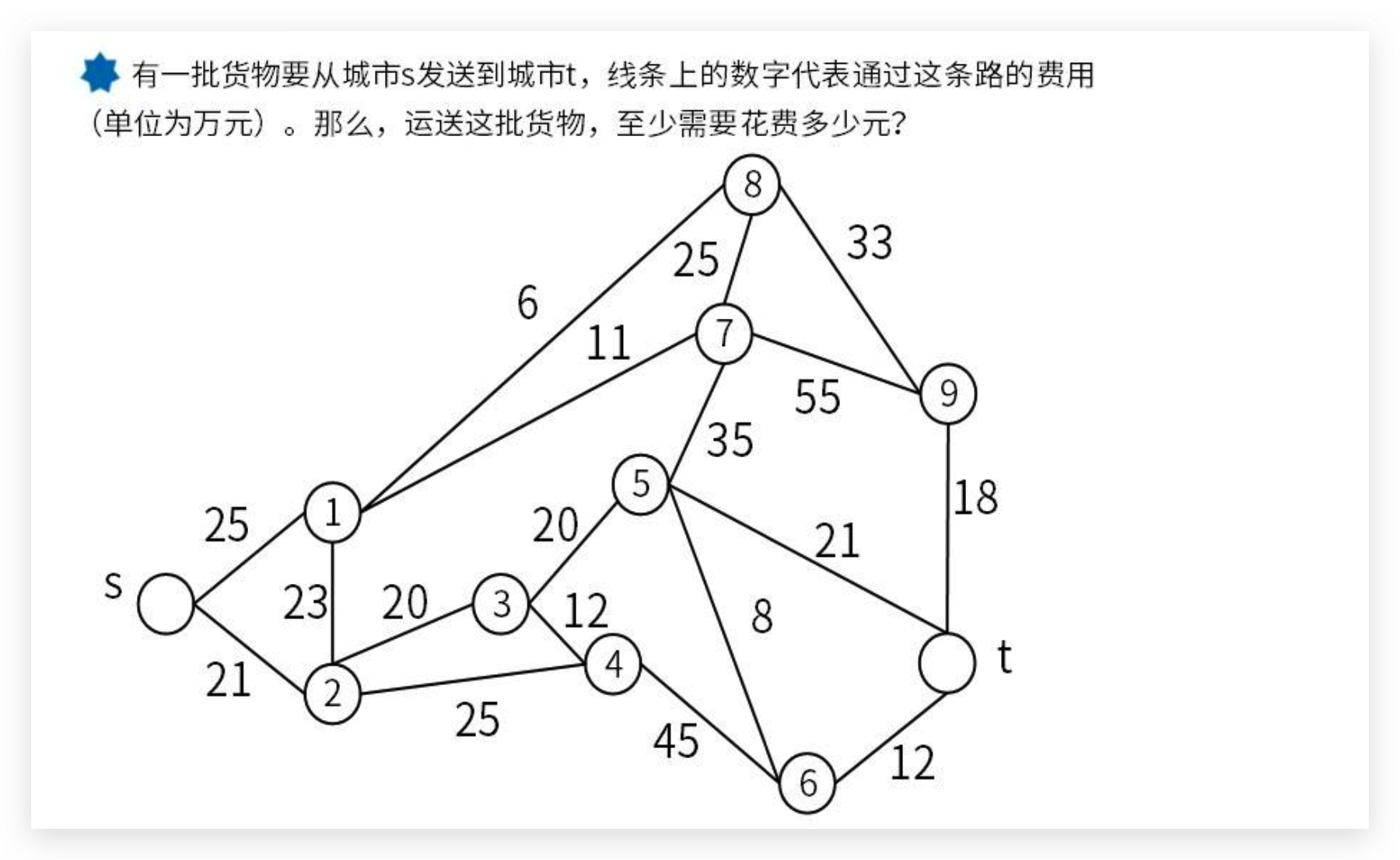
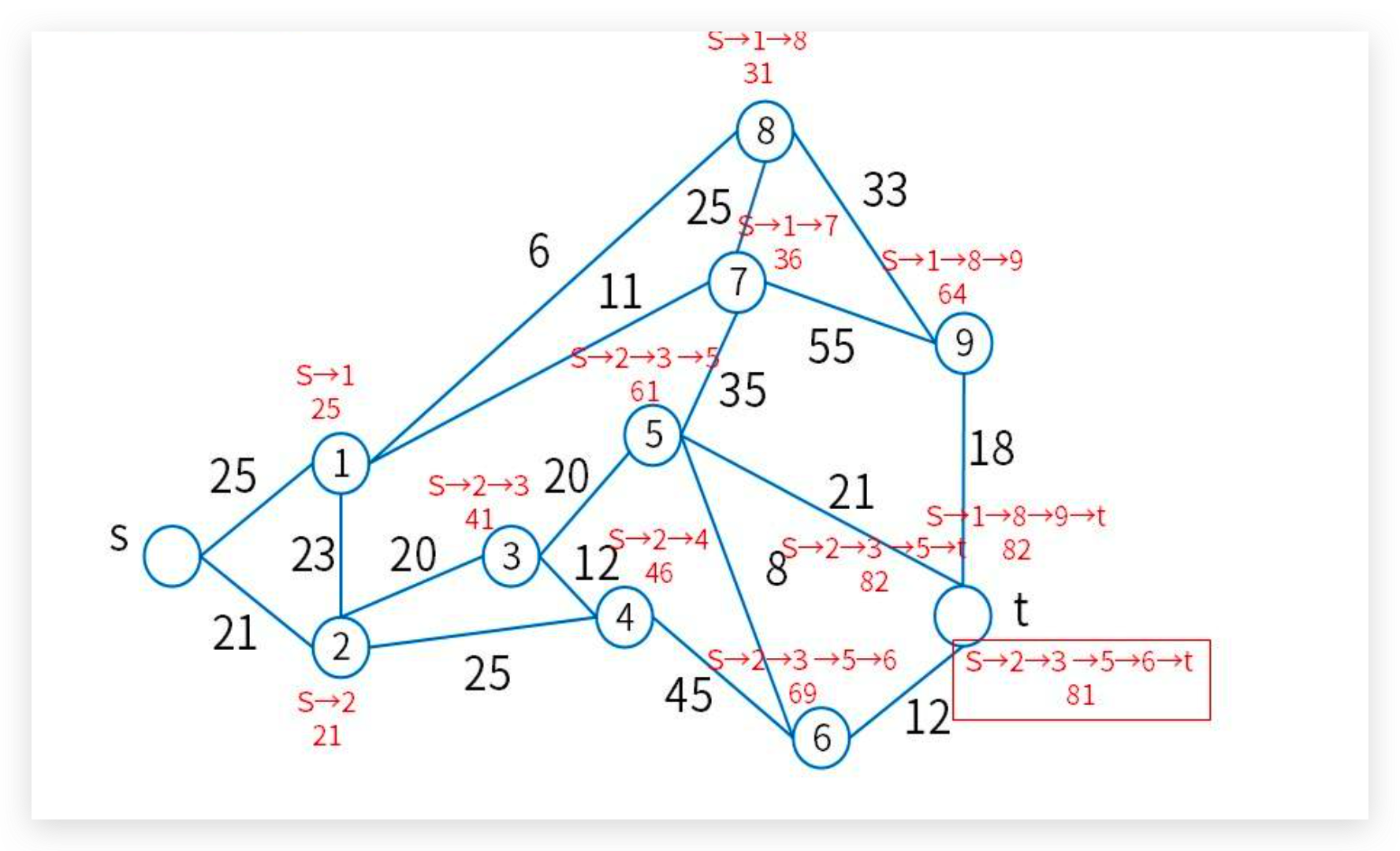










![(我的创作纪念日)[MySQL]数据库原理7——喵喵期末不挂科](https://img-blog.csdnimg.cn/direct/c88efe5d838e43dd83cc8b8918390a3f.png)
