GPT1
文章目录
- GPT1
- 前言
- 正文
- 模型架构
- 无监督学习
- 有监督学习
- 处理不同特定任务
- 实验
- 训练细节
- 实验结果
- 分析
- 预训练层参数转移的影响
- zero-shot的表现
- 消融实验
- 总结
前言
GPT1,出自于OpenAI的论文《Improving Language Understanding by Generative Pre-Training》,是最早的将transformer以多层堆叠的方式构成语言模型的模型,其出现时间早于BERT,但二者有一个最大的区别在于BERT只用的是transformer的encoder层,而GPT1只用了transformer的decoder层。除此以外二者在目标函数等地方也有各自的方法,感兴趣的可以自行阅读对比,这里不再展开。
正文
模型架构
GPT1的训练主要分成无监督预训练和有监督微调两部分:
- 无监督预训练指的是现在大规模语料下,训练一个语言模型;
- 有监督微调指的是基于下游任务的标注数据进行模型参数调整。
无监督学习
给一组无监督学习语料的tokens:
U
=
{
u
1
,
u
2
,
.
.
.
,
u
n
}
\cal{U}=\{u_1, u_2,...,u_n\}
U={u1,u2,...,un},我们以语言模型的目标函数作为目标,最大化其似然函数:
L
1
(
U
)
=
Σ
i
log
P
(
u
i
∣
u
i
−
k
,
.
.
.
,
u
i
−
1
;
Θ
)
(1)
L_1(\cal{U})=\Sigma_{i}{\log{\it{P}}(u_i|u_{i-k},...,u_{i-1};\Theta)} \tag{1}
L1(U)=ΣilogP(ui∣ui−k,...,ui−1;Θ)(1)
其中
k
k
k表示窗口大小,
P
P
P表示由参数
Θ
\Theta
Θ决定的神经网络所输出的条件概率值。
这里再简单用公式阐述下前言中提到的本文核心的多头transformer-decoder层:
h
0
=
U
W
e
+
W
p
h
l
=
t
r
a
n
s
f
o
r
m
e
r
_
b
l
o
c
k
(
h
l
−
1
)
,
∀
i
∈
[
1
,
n
]
P
(
u
)
=
s
o
f
t
m
a
x
(
h
n
W
e
T
)
(2)
h_0=UW_e+W_p\\h_l=\mathrm{transformer\_block}\mathit (h_{l-1}),\forall{i\in[1,n]}\\P(u)=\mathrm{softmax}(\mathit h_nW_e^T)\tag{2}
h0=UWe+Wphl=transformer_block(hl−1),∀i∈[1,n]P(u)=softmax(hnWeT)(2)
其中
U
=
(
u
−
k
,
.
.
.
,
u
−
1
)
U=(u_{-k},...,u_{-1})
U=(u−k,...,u−1)是文本的tokens向量,
n
n
n是transformer的层数,
W
e
W_e
We是token embedding矩阵,
W
p
W_p
Wp是position embedding矩阵。
有监督学习
在完成了无监督学习后,我们希望在有标签的数据集上对模型进行有监督的微调。我们定义标注数据集为
C
\cal{C}
C,对于每一组序列tokens:
x
=
{
x
1
,
x
2
,
.
.
.
,
x
m
}
x=\{x^1,x^2,...,x^m\}
x={x1,x2,...,xm},都对应一个标签
y
y
y。输入
x
x
x通过预训练模型后得到最后一层transformer层的隐向量
h
l
m
h_l^m
hlm,通过一个线性层+softmax预测标签y:
P
(
y
∣
x
1
,
.
.
.
,
x
m
)
=
s
o
f
t
m
a
x
(
h
l
m
W
y
)
(3)
P(y|x^1,...,x^m)=\mathrm{softmax}(h_l^mW_y)\tag{3}
P(y∣x1,...,xm)=softmax(hlmWy)(3)
由此我们的目标是使下面这个目标函数最大化:
L
2
(
C
)
=
Σ
(
x
,
y
)
(
l
o
g
P
(
y
∣
x
1
,
.
.
.
,
x
m
)
)
(4)
L_2(\cal{C})=\Sigma_{(x,y)}(\mathrm{log}\it P(y|x^1,...,x^m))\tag{4}
L2(C)=Σ(x,y)(logP(y∣x1,...,xm))(4)
我们发现在在有监督微调的训练中,如果加入语言模型的目标函数,可以有两个好处:(a)使得有监督模型具备更强的生成能力;(b)加快训练的收敛。所以我们如下定义最终的目标函数:
L
3
(
C
)
=
L
1
(
C
)
+
λ
∗
L
2
(
C
)
L_3(\cal{C})=L_1(\cal{C})+\lambda*L_2(\cal{C})
L3(C)=L1(C)+λ∗L2(C)
处理不同特定任务
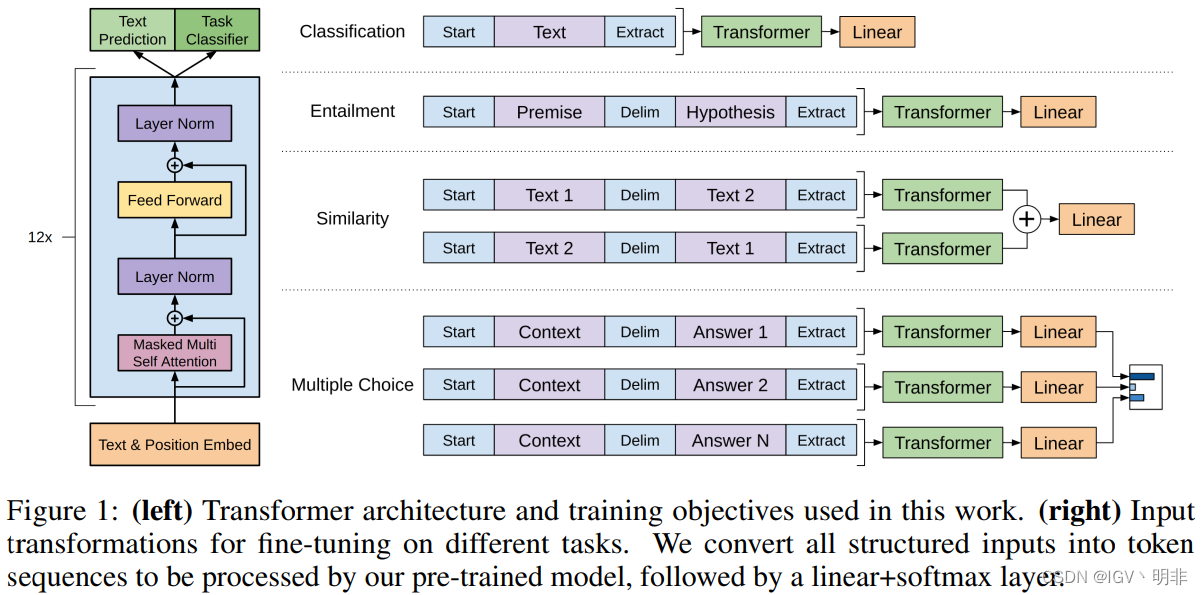
对于某些任务,如文本分类,我们可以直接如上所述对模型进行微调。某些其他任务,如QA或文本蕴含,其具有结构化输入,如有序的句子对,或文档、问题和答案的三元组。因为我们的预训练模型是在连续的文本序列上训练的,我们需要一些修改才能将其应用于这些任务。先前的工作提出了基于迁移学习的学习任务特定架构,这种方法重新引入了大量特定于任务的定制,对这些额外的架构组件使用迁移学习。相反,我们在这里不这么做,我们使用遍历样式方法,将结构化输入转换为预训练模型可以处理的格式,这些输入转换让我们避免对不同的任务都要进行任务架构改变。下面我们通过一些例子和一个示意图来解释。
- 文本蕴含:我们将前提和假设的序列token按照顺序给拼接起来(可以用$等特殊标识符)
- 文本相似度:将两个句子拼接起来,但由于相似度不存在前后关系,所以我们把句子以a b 和 b b和b b和ba两种方式均拼接一遍,最后将输出的两个 h l m h_l^m hlm逐个元素相加后再进入线性输出层。
具体示例如下图所示,包括了transform层的基本结构(mask多头attention+残差链接+LaryerNorm+FNN)
实验
训练细节
包括数据获取,数据处理,无监督训练参数设置,有监督训练参数设置等,这里不一一介绍。
实验结果
首先展示在Natural Language Inference常见公开数据集上的结果,以及和当前一些sota方法的效果对比:
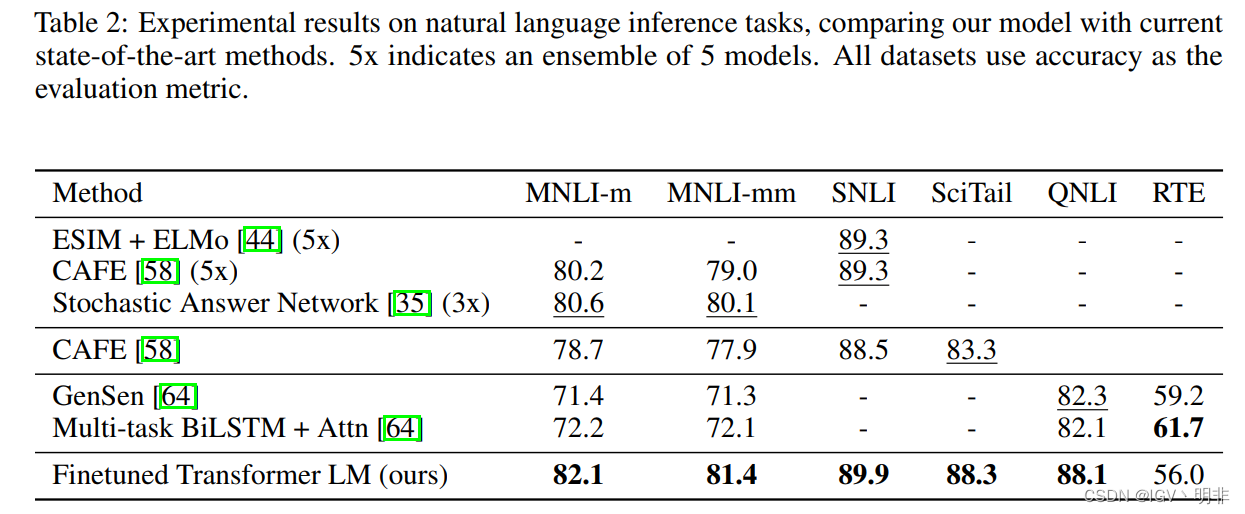 然后是在Question answering and commonsense reasoning常见公开数据集上的结果,以及和当前方法的效果对比:
然后是在Question answering and commonsense reasoning常见公开数据集上的结果,以及和当前方法的效果对比:
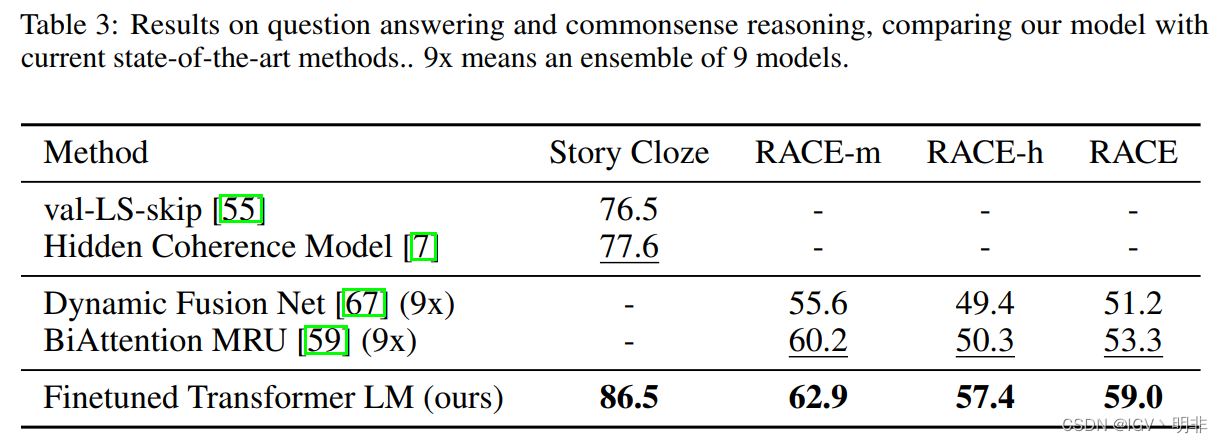 还有文本相似度任务以及分类任务等:
还有文本相似度任务以及分类任务等:
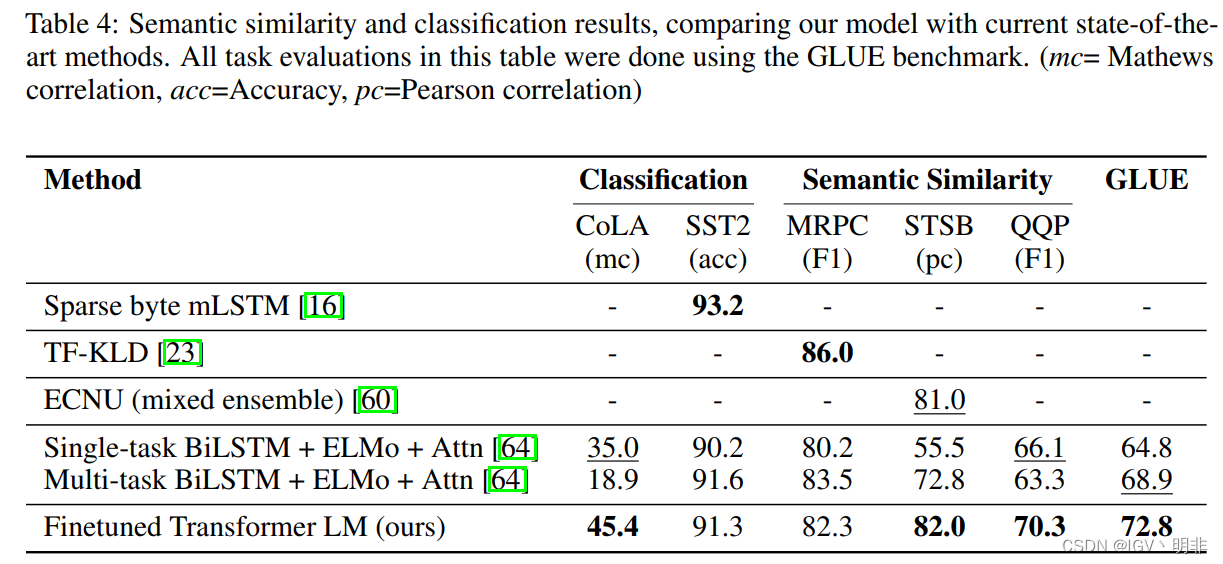
分析
预训练层参数转移的影响
我们想观察下从预训练模型中转移参数值作为有监督学习模型的初始化参数,到底会有多少提升:
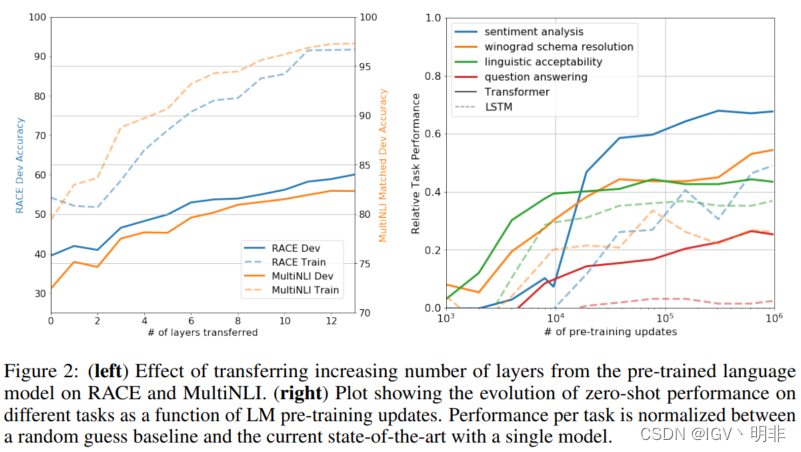 可以看到,如果将模型的参数随机初始化,并在RACE和MultiNLI任务上进行训练,在验证集上的acc只有40%左右,但是如果将预训练模型的参数迁移过来的话,可以使acc提升到80+,这个提升确实十分明显。
可以看到,如果将模型的参数随机初始化,并在RACE和MultiNLI任务上进行训练,在验证集上的acc只有40%左右,但是如果将预训练模型的参数迁移过来的话,可以使acc提升到80+,这个提升确实十分明显。
zero-shot的表现
我们想更好的理解为什么基于transformer的预训练语言模型是有效的。一个假设说一方面,底层的生成模型学习如何在许多我们通常评估的任务上表现更好,以此来提高语言模型的能力;另一方面,transformer比LSTM在迁移学习上表现得更好。我们设计了一系列启发式解决方案,使用底层生成模型执行任务,而无需监督微调,并将其进行饿了可视化(Figure 2的右图)。
我们观察到这些启发式算法的表现是稳定的,并且随着训练而稳步增加,这表明生成性预训练支持多种任务相关功能的学习。另外我们也观察到LSTM在各种任务上的表现参差不齐,而且整体也不如transormer。
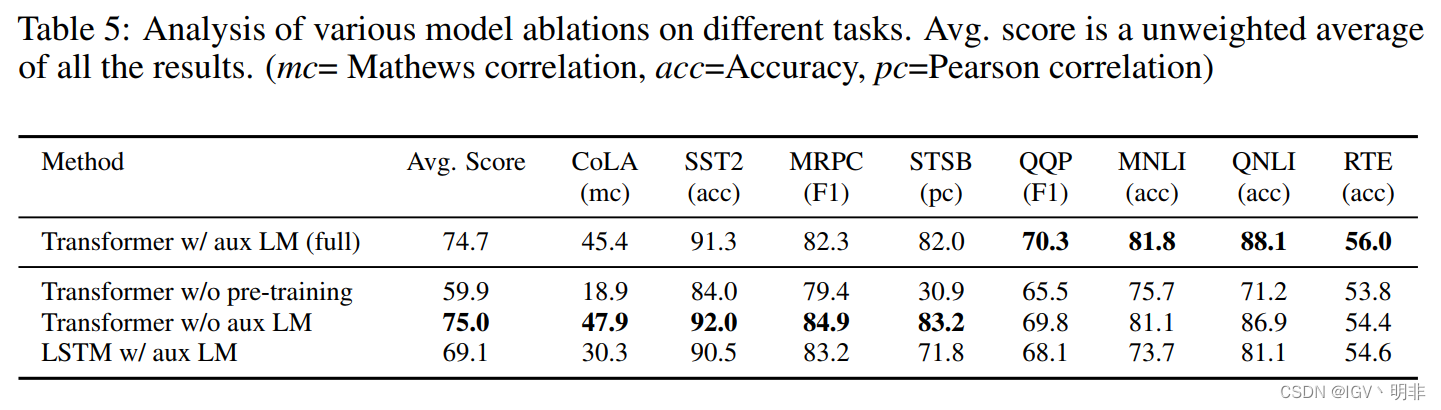
消融实验
最后是喜闻乐见的消融实验,主要关注有监督训练的时候加入aux目标函数对效果的影响,顺便对比了下finetune后的模型、没有进行finetune模型和LSTM模型的效果。transformer的效果显然好于LSTM,不必多说。但加入aux后finetune的模型在不同的任务上表现不一,但总的来说有一个趋势:在大数据集下,加入aux会提升最终的finetune效果,但是小数据集下,不加入aux目标函数效果更好。
总结
我们通过单一任务不可知(task-agnostic)模型实现了一个强大的自然语言理解框架,主要包括生成性预训练和区分性微调两部分。通过在长的连续文本的不同语料库上进行预训练,我们的模型获得了重要的世界知识和处理长距离依赖的能力,然后成功地将这些知识和能力转移到解决诸如问题回答、语义相似性评估、文本蕴含、文本分类等任务上,改善了我们研究的12个数据集中的9个数据集的sota。
长期以来,使用无监督(预)训练来提高辨别性任务的性能一直是机器学习研究的一个重要目标。我们的工作表明,实现显著的性能提升确实是可能的,并提供了关于哪些模型(Transformers)和数据集(具有长范围依赖关系的文本)最适合这种方法的一些提示。我们希望这将有助于对自然语言理解和其他领域的无监督学习进行新的研究,进一步提高我们对无监督学习如何工作的理解。














![最大比例(数论 最大公约数 辗转相减法)[第七届蓝桥杯省赛C++A/B组]](https://img-blog.csdnimg.cn/5c2ddd00d04846b7871f038f800c3635.png)