分类模型绘制决策边界、过拟合、评价指标

news2025/6/23 12:42:06

文章目录

  • 1、线性逻辑回归决策边界
    • 1.2、使用自定义函数绘制决策边界
    • 1.3、三分类的决策边界
    • 1.4、多项式逻辑回归决策边界
  • 2、过拟合和欠拟合
    • 2.2、欠拟合
    • 2.3、过拟合
  • 3、学习曲线
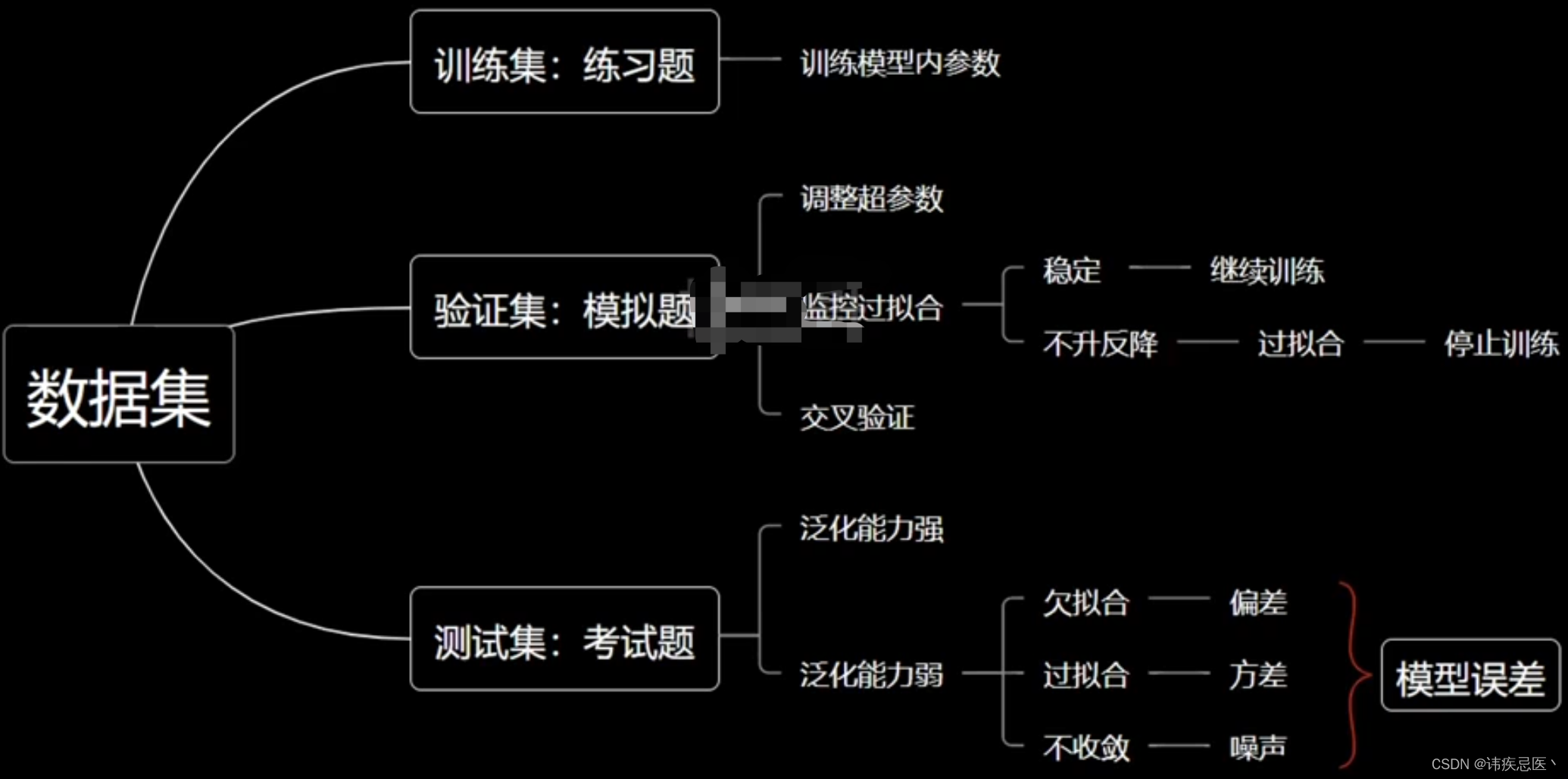
  • 4、交叉验证
  • 5、泛化能力
  • 6、混淆矩阵
  • 7、PR曲线和ROC曲线

x2可以用x1来表示
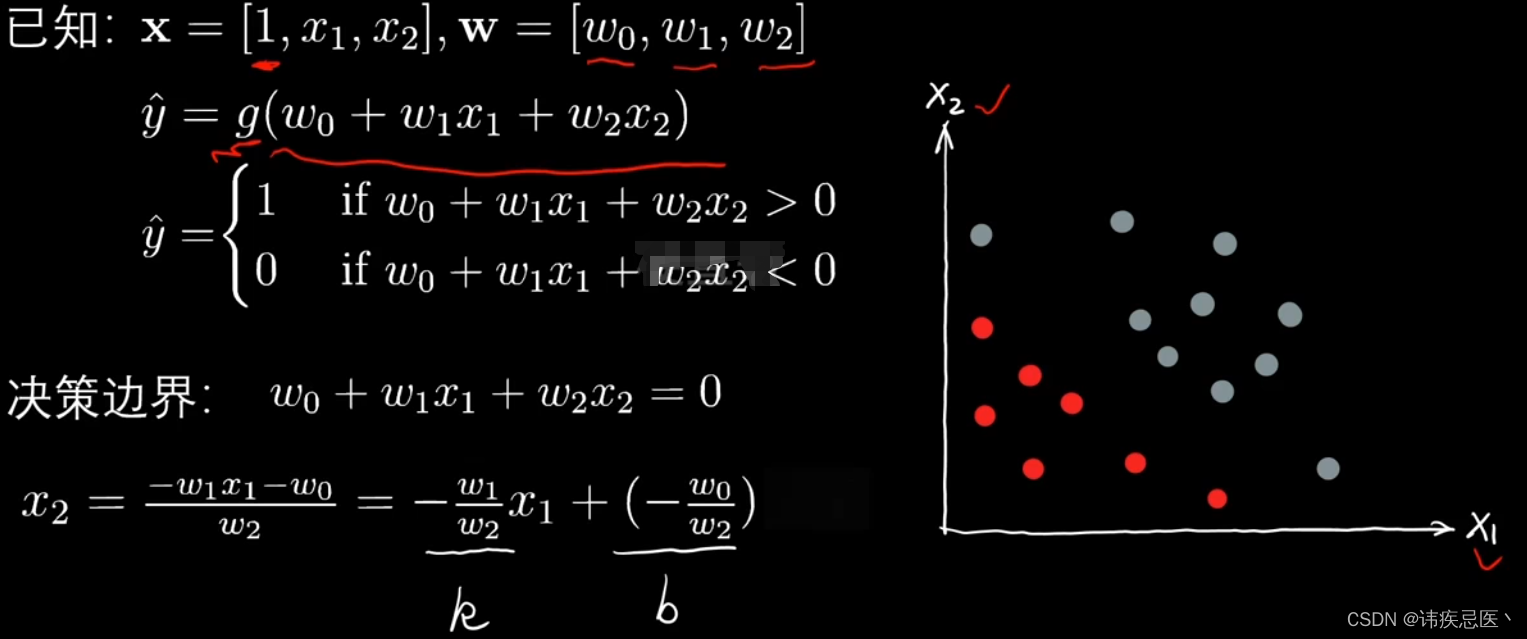
在这里插入图片描述

1、线性逻辑回归决策边界

# 逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
x,y = make_classification(
    n_samples=200,# 样本数
    n_features=2,# 特征数
    n_redundant=0,# 冗余特指数
    n_classes=2,# 类型
    n_clusters_per_class=1,# 族设为1
    random_state=1024
)
x.shape,y.shape

x_train,x_test,y_train,y_test = train_test_split(x,y,train_size=0.7,random_state=1024,stratify=y)
plt.scatter(x_train[:,0],x_train[:,1],c=y_train)

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(x_train,y_train)
clf.score(x_test,y_test)
# clf.predict(x_test)

x1 = np.linspace(-4,4,1000)
x2 = (-clf.coef_[0][0] * x1 -clf.intercept_)/clf.coef_[0][1]
plt.scatter(x_train[:,0],x_train[:,1],c=y_train)
plt.scatter(x1,x2)
plt.show()

在这里插入图片描述

1.2、使用自定义函数绘制决策边界

很多时候不只是画一条线

def decision_boundary_plot(X, y, clf):
    axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
    axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
    
    x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
    z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
    z = z.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])

    plt.contourf(x1, x2, z, cmap=custom_cmap)
    plt.scatter(X[:,0], X[:,1], c=y)
    plt.show()


decision_boundary_plot(x, y ,clf)

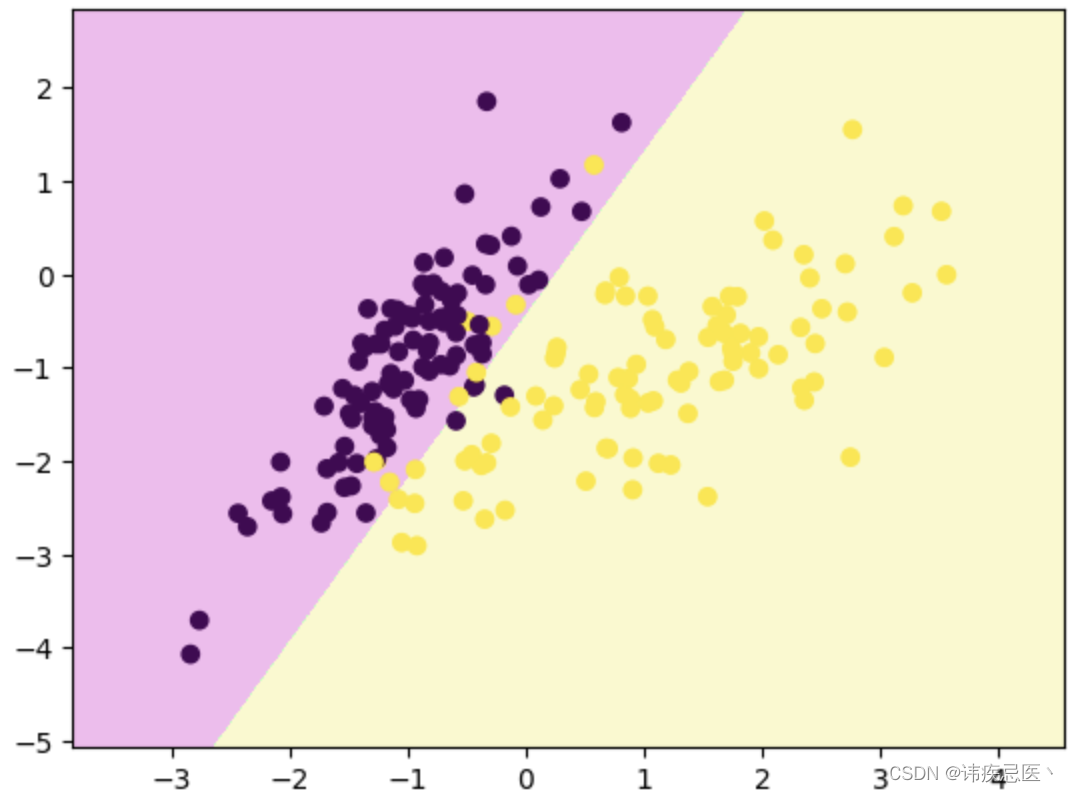
在这里插入图片描述

1.3、三分类的决策边界

from sklearn import datasets
iris = datasets.load_iris()
x = iris.data[:,:2]
y = iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=666)
plt.scatter(x_train[:,0], x_train[:,1], c = y_train)
plt.show()

clf.score(x_test, y_test)
decision_boundary_plot(x, y, clf)

在这里插入图片描述

1.4、多项式逻辑回归决策边界

np.random.seed(0)
x = np.random.normal(0, 1, size=(200, 2))
y = np.array((x[:,0]**2+x[:,1]**2)<2, dtype='int')
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size = 0.7, random_state = 233, stratify = y)
plt.scatter(x_train[:,0], x_train[:,1], c = y_train)
plt.show()


from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
clf_pipe = Pipeline([
        ('poly', PolynomialFeatures(degree=2)),
        ('std_scaler', StandardScaler()),
        ('log_reg', LogisticRegression())
    ])

clf_pipe.fit(x_train, y_train)
decision_boundary_plot(x, y, clf_pipe)

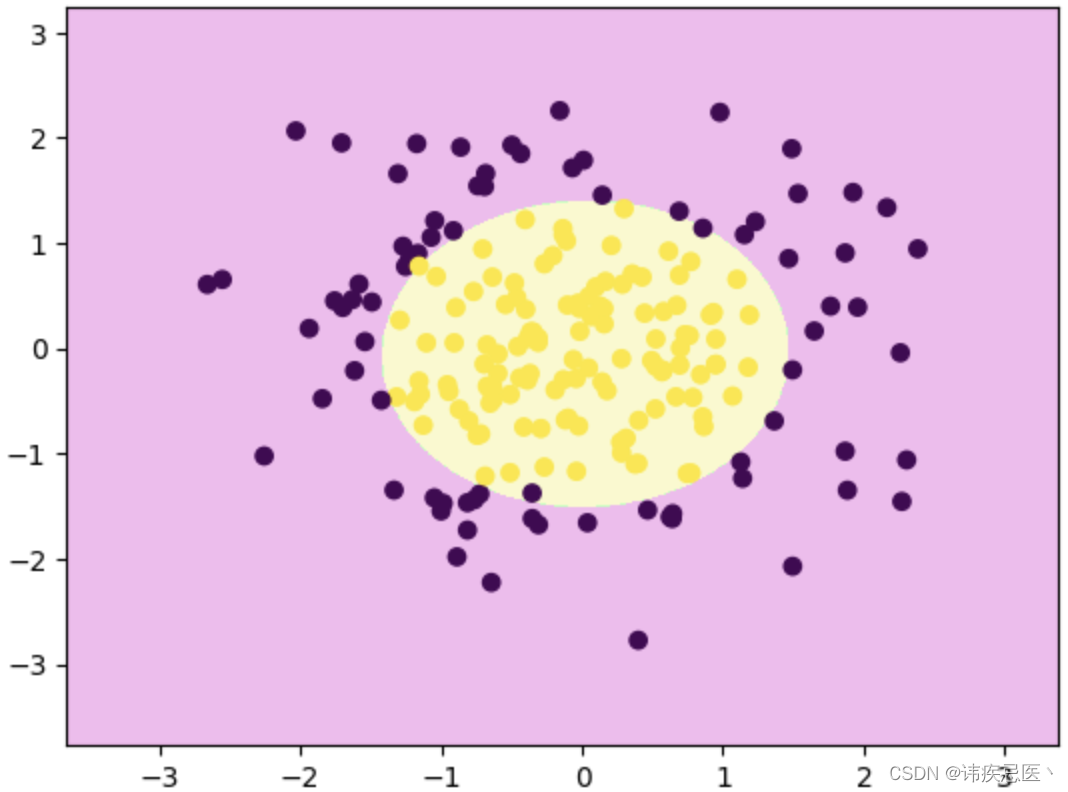
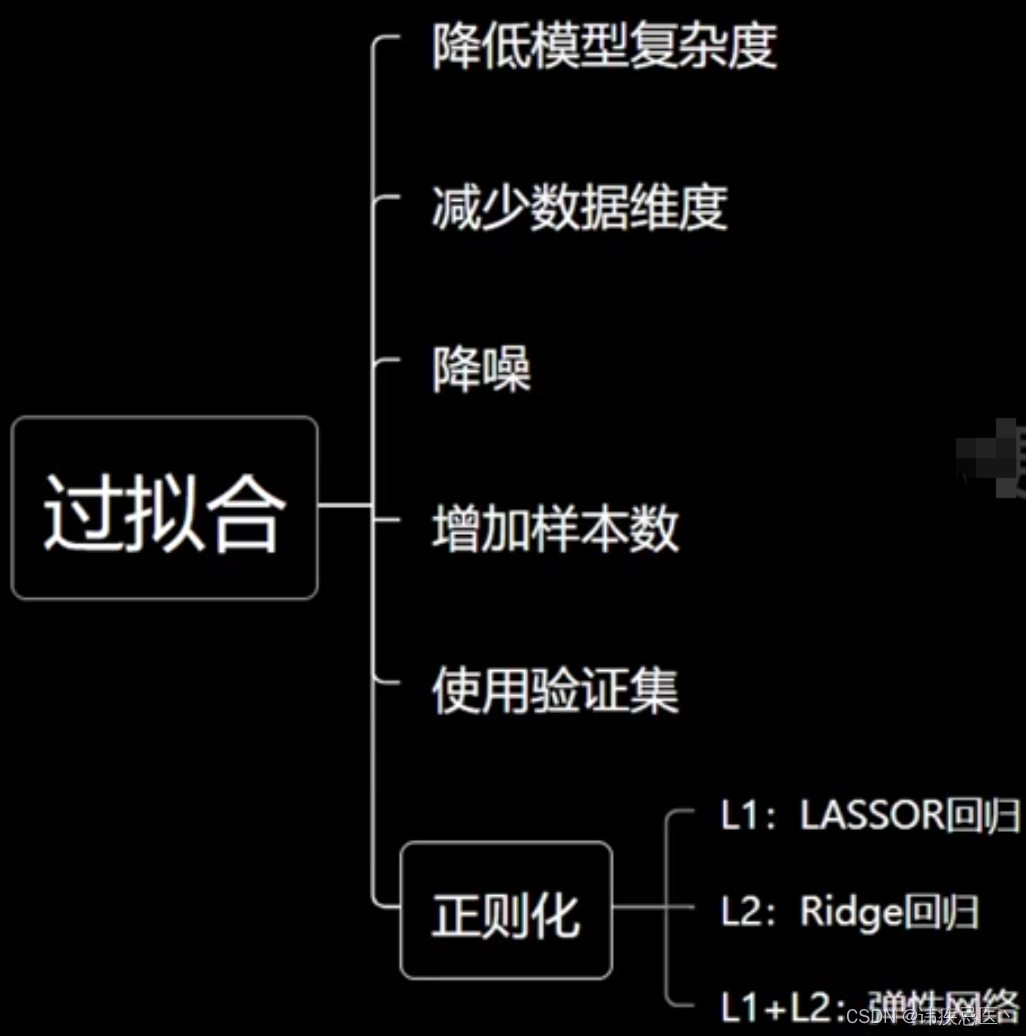
在这里插入图片描述

2、过拟合和欠拟合

2.2、欠拟合

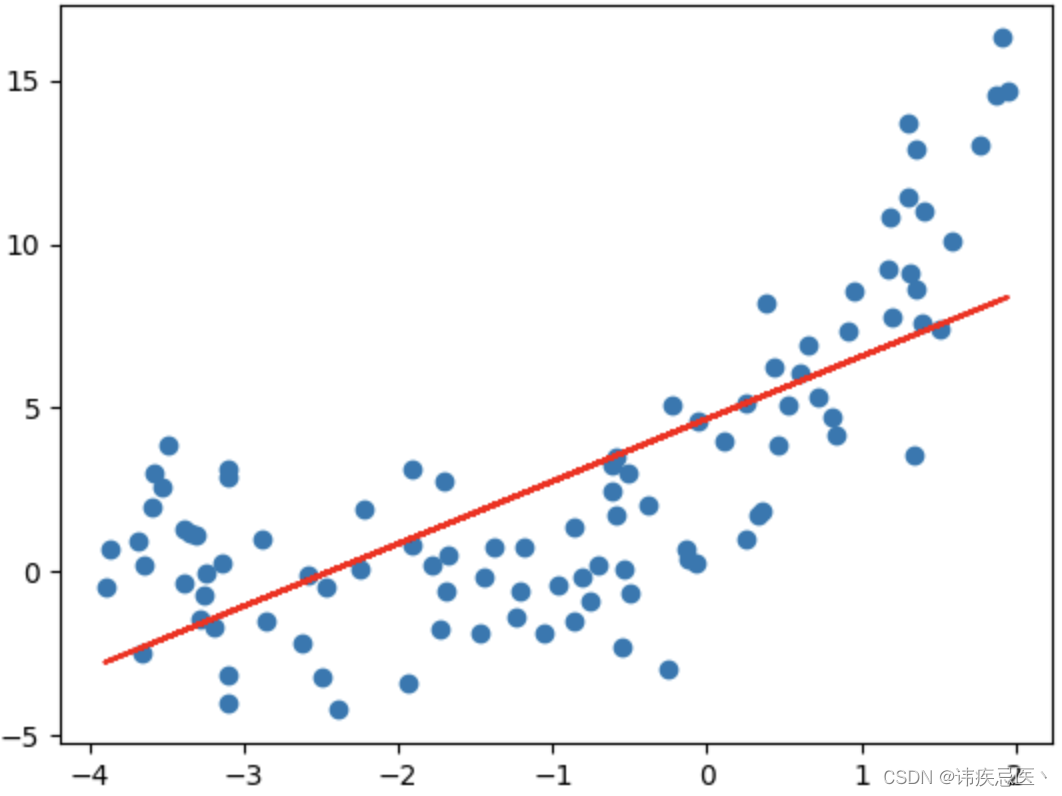
在这里插入图片描述
特征维度不足，模型复杂度角度，无法学习到数据背后的规律，使用一元线性回归拟合抛物线数据自然会导致欠拟合

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(233)
x = np.random.uniform(-4, 2, size = (100))
y = x ** 2 + 4 * x + 3 + 2 * np.random.randn(100)

X = x.reshape(-1, 1)

plt.scatter(x,y)
plt.show()

from sklearn.linear_model import LinearRegression
linear_regression = LinearRegression()
linear_regression.fit(X, y)
y_predict = linear_regression.predict(X)
plt.scatter(x, y)
plt.plot(x, y_predict, color = 'red')
plt.show()

2.3、过拟合

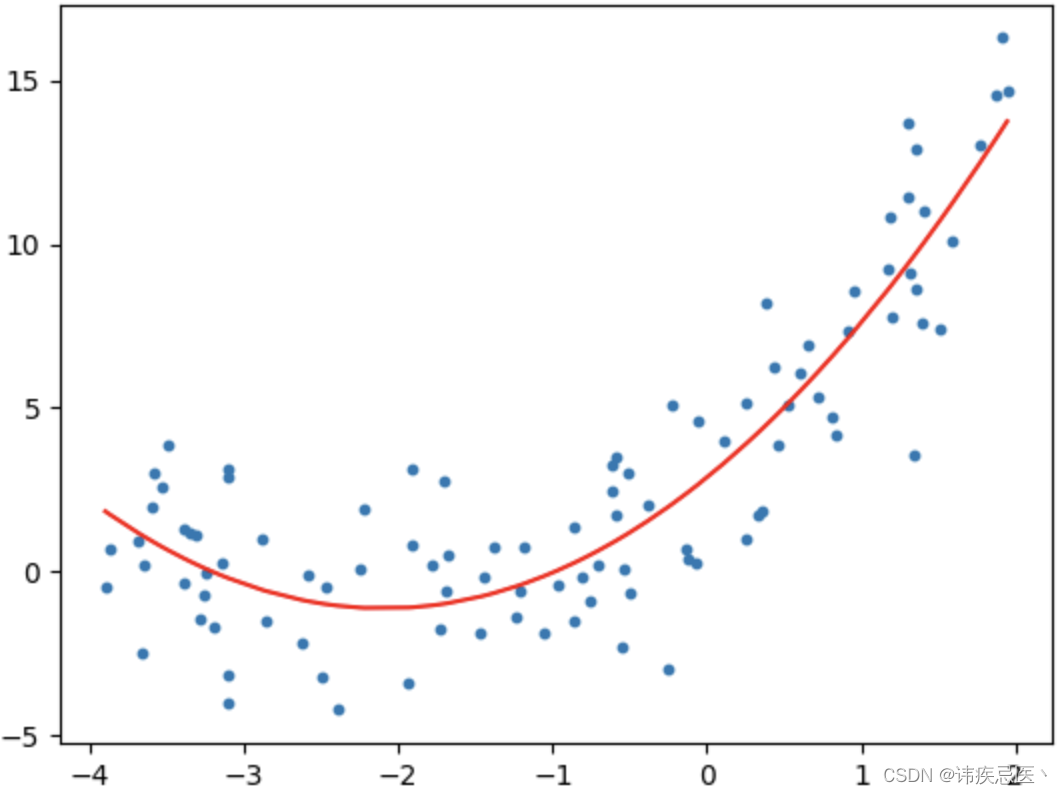
在这里插入图片描述

from sklearn.preprocessing import PolynomialFeatures
polynomial_features = PolynomialFeatures(degree=2)
X_poly = polynomial_features.fit_transform(X)
linear_regression = LinearRegression()
linear_regression.fit(X_poly,y)
y_predict = linear_regression.predict(X_poly)
plt.scatter(x,y,s=10)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='red')
plt.show()

# 另外一种方式
X_new = np.linspace(-5,3,200).reshape(-1,1)
X_new_poly = polynomial_features.fit_transform(X_new)
y_predict = linear_regression.predict(X_new_poly)
plt.scatter(x,y,s=10)
plt.plot(X_new,y_predict,color='red')
plt.show()
print("degree:",2,"score:",linear_regression.score(X_poly,y))

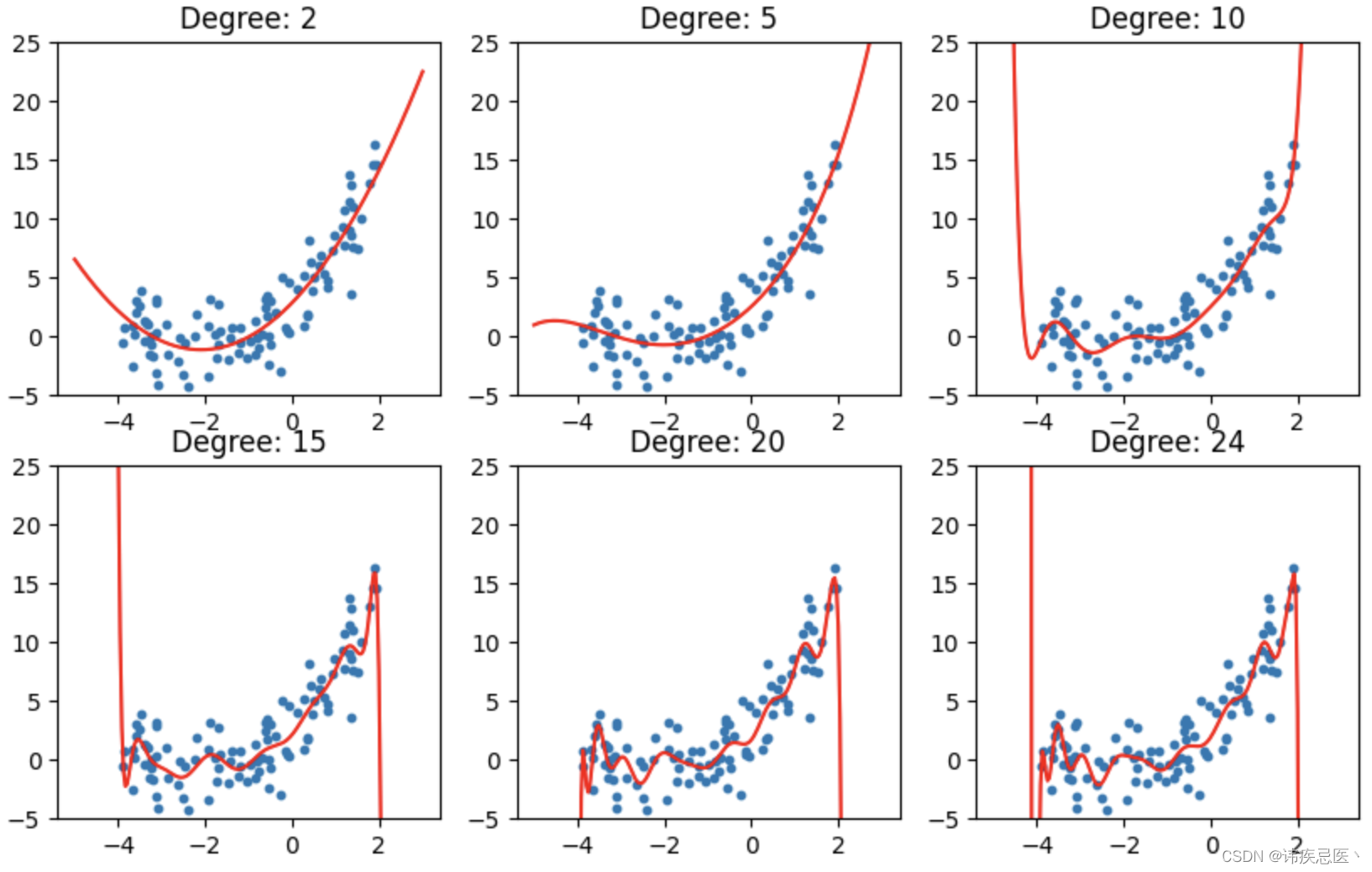
在这里插入图片描述
下面三种情况，曲线越来越复杂，与我们的数据相差很远，如果划分了训练集测试机，往往就会在训练集上效果很好，在测试集上效果很差，通俗来讲就是死记了所有习题，但是一考试分数就很低，泛化能力太差。

plt.rcParams["figure.figsize"] = (10, 6)

degrees = [2, 5, 10, 15, 20, 24]
for i, degree in enumerate(degrees):
    polynomial_features = PolynomialFeatures(degree = degree)
    X_poly = polynomial_features.fit_transform(X)
    
    linear_regression = LinearRegression()
    linear_regression.fit(X_poly, y)
    
    X_new = np.linspace(-5, 3, 200).reshape(-1, 1)
    X_new_poly = polynomial_features.fit_transform(X_new)
    y_predict = linear_regression.predict(X_new_poly)
    
    plt.subplot(2, 3, i + 1)
    plt.title("Degree: {0}".format(degree))
    plt.scatter(x, y, s = 10)
    plt.ylim(-5, 25)
    plt.plot(X_new, y_predict, color = 'red')
    
    print("Degree:", degree, "Score:", linear_regression.score(X_poly, y))
    
plt.show()

3、学习曲线

在这里插入图片描述
从曲线图可以看出来，degree为1的时候误差值比较大，明显是欠拟合状态，为2的时候效果比较好，为5，20的时候明显过拟合状态，训练误差比较小，但是测试误差很大。
在这里插入图片描述

from sklearn.metrics import mean_squared_error

plt.rcParams["figure.figsize"] = (12, 8)

degrees = [1, 2, 5, 20]
for i, degree in enumerate(degrees):
    polynomial_features = PolynomialFeatures(degree = degree)
    
    X_poly_train = polynomial_features.fit_transform(x_train.reshape(-1, 1))
    X_poly_test = polynomial_features.fit_transform(x_test.reshape(-1, 1))
    
    train_error, test_error = [], []
    for k in range(len(x_train)):
        linear_regression = LinearRegression()
        linear_regression.fit(X_poly_train[:k + 1], y_train[:k + 1])

        y_train_pred = linear_regression.predict(X_poly_train[:k + 1])
        train_error.append(mean_squared_error(y_train[:k + 1], y_train_pred))

        y_test_pred = linear_regression.predict(X_poly_test)
        test_error.append(mean_squared_error(y_test, y_test_pred))
    
    plt.subplot(2, 2, i + 1)
    plt.title("Degree: {0}".format(degree))
    plt.ylim(-5, 50)
    plt.plot([k + 1 for k in range(len(x_train))], train_error, color = "red", label = 'train')
    plt.plot([k + 1 for k in range(len(x_train))], test_error, color = "blue", label = 'test')
    plt.legend()

plt.show()

4、交叉验证

有没有一种可能就是，模型正好在测试数据集上跑的效果正常，而真实情况是过拟合的，只是没有跑出来，这样的情况下准确性和学习曲线上看似良好，一跑真实数据效果就很差。
解决方法：
多抽几组数据来验证，比如：训练集比作练习题，验证机比作模拟测试，测试机比作考试题。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

iris = load_iris()
x = iris.data
y = iris.target

x_train, x_test, y_train, y_test = train_test_split(x, y, train_size = 0.7, random_state = 233, stratify = y)
x_train.shape, x_test.shape, y_train.shape, y_test.shape

from sklearn.model_selection import cross_val_score

neigh = KNeighborsClassifier()
cv_scores = cross_val_score(neigh, x_train, y_train, cv = 5)
print(cv_scores)

best_score = -1
best_n = -1
best_weight = ''
best_p = -1
best_cv_scores = None
for n in range(1, 20):
    for weight in ['uniform', 'distance']:
        for p in range(1, 7):
            neigh = KNeighborsClassifier(
                n_neighbors = n,
                weights = weight,
                p = p
            )
            cv_scores = cross_val_score(neigh, x_train, y_train, cv = 5)
            score = np.mean(cv_scores)
            if score > best_score:
                best_score = score
                best_n = n
                best_weight = weight
                best_p = p
                best_cv_scores = cv_scores

print("n_neighbors:", best_n)
print("weights:", best_weight)
print("p:", best_p)
print("score:", best_score)
print("best_cv_scores:", best_cv_scores)

5、泛化能力

机器学习算法对新鲜事物样本的适应能力，奥卡姆剃刀法则：能简单别复杂，泛化理论：衡量模型复杂度
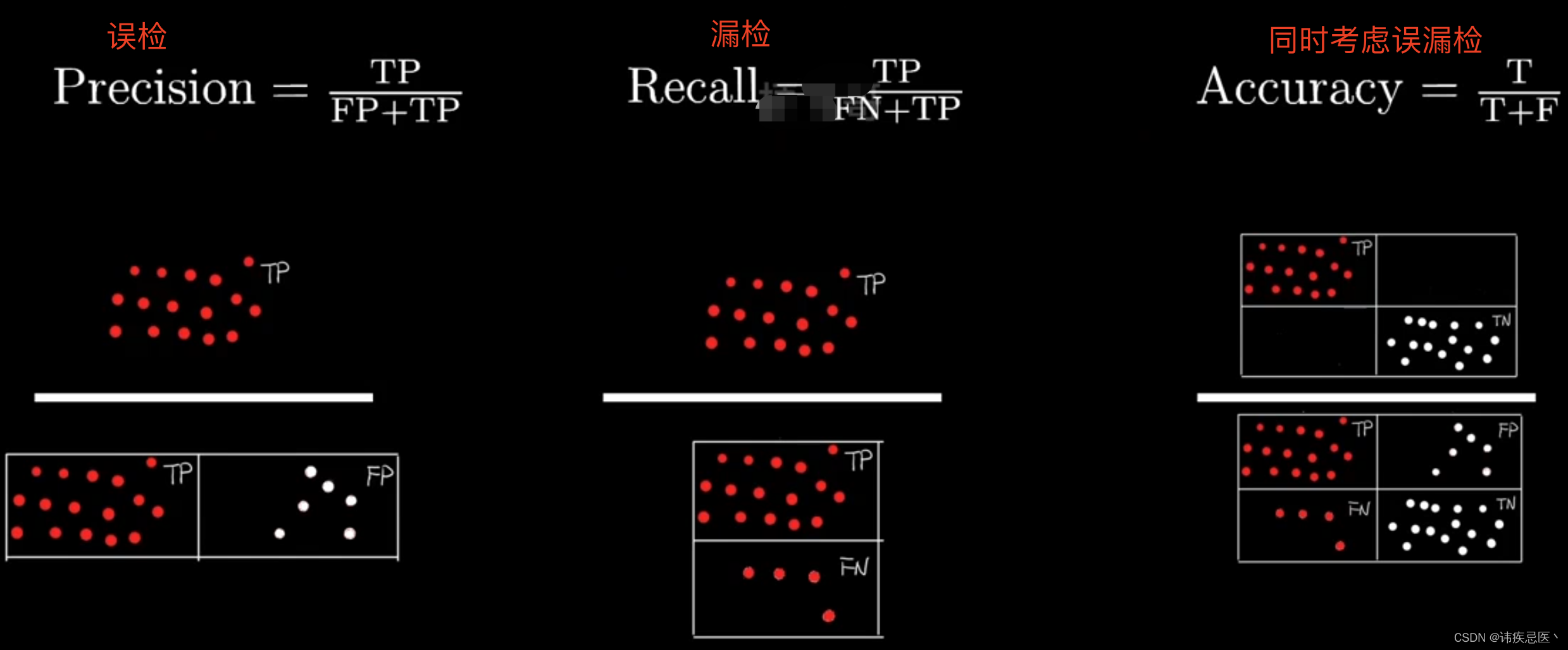
在这里插入图片描述
在这里插入图片描述

6、混淆矩阵

在这里插入图片描述
在这里插入图片描述
F1 Score
在这里插入图片描述

iris = datasets.load_iris()
X = iris.data
y = iris.target.copy()

# 变成二分类
y[y!=0] = 1

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

logistic_regression = LogisticRegression()
logistic_regression.fit(X_train,y_train)
y_predict = logistic_regression.predict(X_test)

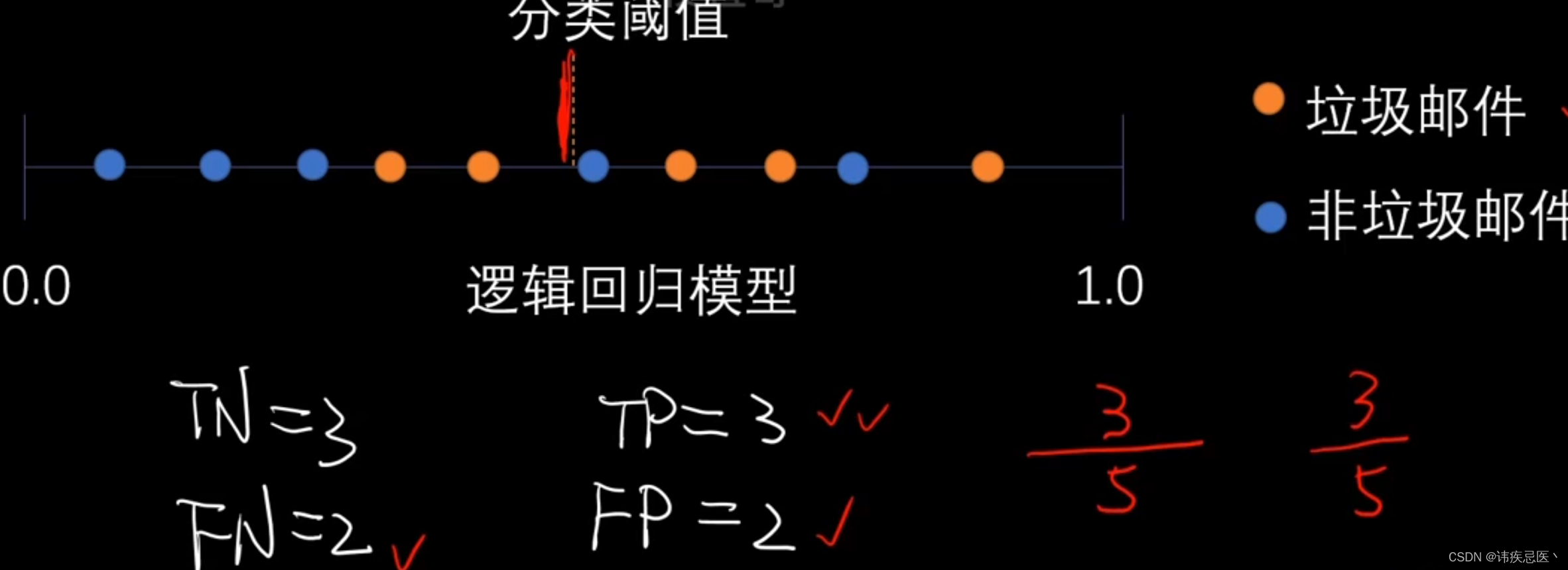
TN = np.sum((y_predict==0)&(y_test==0))
TN

FP = np.sum((y_predict==1)&(y_test==0))
FP

FN = np.sum((y_predict==0)&(y_test==1))
FN

TP = np.sum((y_predict==1)&(y_test==1))
TP

confusion_matrix = np.array([
    [TN, FP],
    [FN, TP]
])

confusion_matrix

precision = TP/ (TP+FP)
precision

recall = TP/(FN+TP)
recall

f1_score = 2*precision*recall /(precision+recall)
f1_score

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test,y_predict)

from sklearn.metrics import precision_score
precision_score(y_test,y_predict)

from sklearn.metrics import recall_score
recall_score(y_test,y_predict)

from sklearn.metrics import f1_score
f1_score(y_test,y_predict)

7、PR曲线和ROC曲线

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target.copy()

# 转化为二分类问题
y[y!=0] = 1

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

logistic_regression = LogisticRegression()
logistic_regression.fit(X_train,y_train)
y_predict = logistic_regression.predict(X_test)
y_predict

decision_scores = logistic_regression.decision_function(X_test)
decision_scores

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score

precision_scores = []
recall_scores = []
thresholds = np.sort(decision_scores)
for threshold in thresholds:
    y_predict = np.array(decision_scores>=threshold,dtype='int')
    precision = precision_score(y_test,y_predict)
    recall = recall_score(y_test,y_predict)
    precision_scores.append(precision)
    recall_scores.append(recall) 
    
plt.plot(thresholds, precision_scores, color='r',label="precision")
plt.plot(thresholds, recall_scores, color='b',label="recall")
plt.legend()
plt.show()

plt.plot(recall_scores,precision_scores)
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.show()

sklearn中实现

# sklearn中
from sklearn.metrics import precision_recall_curve

precision_scores, recall_scores,thresholds =  precision_recall_curve(y_test,decision_scores)

plt.plot(thresholds, precision_scores[:-1], color='r',label="precision")
plt.plot(thresholds, recall_scores[:-1], color='b',label="recall")
plt.legend()
plt.show()

plt.plot(recall_scores,precision_scores)
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.show()


# ROC曲线
from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_test,decision_scores)
plt.plot(fpr,tpr)
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.show()

# AUC
from sklearn.metrics import roc_auc_score

auc = roc_auc_score(y_test,decision_scores)
auc

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1584568.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

TQ15EG开发板教程：在MPSOC上运行ADRV9009

TQ15EG开发板教程：在MPSOC上运行ADRV9009

首先需要在github上下载两个文件&#xff0c;本例程用到的文件以及最终文件我都会放在网盘里面&#xff0c; 地址放在最后面。在github搜索hdl选择第一个&#xff0c;如下图所示 GitHub网址&#xff1a;https://github.com/analogdevicesinc/hdl/releases 点击releases选择版…
阅读更多...
Vue 读取后台二进制文件流转为图片显示

Vue 读取后台二进制文件流转为图片显示

Vue 读取后台二进制文件流转为图片显示 后台返回格式 <img :src"payImg" id"image" style"width: 150px;height: 150px;" alt"">axios写法 重点 responseType: ‘blob’ &#xff0c; 使用的是res中的data blob this.$axios.…
阅读更多...
科学计算最新成果！基于多分支物理信息深度算子神经网络的快速通用热仿真模型...

科学计算最新成果！基于多分支物理信息深度算子神经网络的快速通用热仿真模型...

热仿真在各个领域中起着至关重要的作用&#xff0c;通常涉及复杂的偏微分方程&#xff08;PDE&#xff09;仿真以进行热优化。为了解决通过传统方法求解复杂的偏微分方程所面临的挑战&#xff0c;我们利用神经网络进行热预测&#xff0c;尤其是采用深度神经网络作为PDE的通用求…
阅读更多...
HTML5学习记录

HTML5学习记录

简介 超文本标记语言&#xff08;HyperText Markup Language&#xff0c;简称HTML&#xff09;&#xff0c;是一种用于创建网页的标准标记语言。 编辑器 下载传送门https://code.visualstudio.com/ 下载编辑器插件 标题 标题通过 <h1> - <h6> 标签进行定义。 …
阅读更多...
花样鼠标悬停特效

花样鼠标悬停特效

代码&#xff1a; <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><style&…
阅读更多...
头歌-机器学习 第9次实验 随机森林

头歌-机器学习 第9次实验 随机森林

第1关&#xff1a;Bagging 任务描述 本关任务&#xff1a;补充 python 代码&#xff0c;完成 BaggingClassifier 类中的 fit 和 predict 函数。请不要修改 Begin-End 段之外的代码。 相关知识 为了完成本关任务&#xff0c;你需要掌握&#xff1a; 什么是 Bagging&#xf…
阅读更多...
python 有哪些函数

python 有哪些函数

Python内置的函数及其用法。为了方便记忆&#xff0c;已经有很多开发者将这些内置函数进行了如下分类&#xff1a; 数学运算(7个) 类型转换(24个) 序列操作(8个) 对象操作(7个) 反射操作(8个) 变量操作(2个) 交互操作(2个) 文件操作(1个) 编译执行(4个) 装饰器(3个) …
阅读更多...
PHP自助建站系统，小白也能自己搭建网站

PHP自助建站系统，小白也能自己搭建网站

无需懂代码&#xff0c;用 自助建站 做企业官网就像做PPT一样简单&#xff0c;您可以亲自操刀做想要的效果&#xff01; 自助建站是一款简单、快捷、高效的工具&#xff0c;可以帮助您制作响应式网站。我们的自助建站系统&#xff0c;将传统的编码工作转化为直观的拖拽操作和文…
阅读更多...
功能测试_验证两个两位数整数边界数据的求和_边界值分析法

功能测试_验证两个两位数整数边界数据的求和_边界值分析法

验证两个两位数整数边界数据的求和 上点&#xff1a;刚好等于边界的值 &#xff08;取值不考虑开闭区间&#xff09; 离点&#xff1a;刚好小于/大于边界上的值 &#xff08;取值类型看需求&#xff09; 内点&#xff1a;边界范围内的任何取值 &#xff08;取中间的值&#…
阅读更多...
2024年 前端JavaScript 进阶 第4天 End 笔记

2024年 前端JavaScript 进阶 第4天 End 笔记

4.1-内容和浅拷贝 4.2-递归函数 4.3-深拷贝实现 4.4-利用lodash和JSON实现深 4.5-异常处理-throw和try、catch 4.6-普通函数和箭头函数的this 4.7-call方法改变this指向 4.8-apply方法 4.9-bind方法以及总结 4.10-什么是防抖以及底层实现 4.11-什么是节流以及底层实现 4.12-节流…
阅读更多...
【教学类-50-07】20240411“数一数”图片中四种图形出现的数量随机或固定

【教学类-50-07】20240411“数一数”图片中四种图形出现的数量随机或固定

背景需求 今天孩子们点数时&#xff0c;我核对答案&#xff0c;突然发现有两张图片上的三角、正方、椭圆、圆形只有1个&#xff0c;我感觉这个随机的概率有问题。 仔细点数后发现以下代码生成的几何图形数量是相同的 &#xff08;如果三角有3个&#xff0c;那么正方形、圆形…
阅读更多...
LangChain-15 Manage Prompt Size 管理上下文大小，用Agent的方式询问问题，并去百科检索内容，总结后返回

LangChain-15 Manage Prompt Size 管理上下文大小，用Agent的方式询问问题，并去百科检索内容，总结后返回

背景描述 这一节内容比较复杂&#xff1a; 涉及到使用工具进行百科的检索&#xff08;有现成的插件&#xff09;有AgentExecutor来帮助我们执行后续由于上下文过大&#xff0c; 我们通过计算num_tokens&#xff0c;来控制我们的上下文 安装依赖 pip install --upgrade --qu…
阅读更多...
上海亚商投顾：创业板指低开低走 低空经济概念股尾盘拉升

上海亚商投顾：创业板指低开低走 低空经济概念股尾盘拉升

上海亚商投顾前言&#xff1a;无惧大盘涨跌&#xff0c;解密龙虎榜资金&#xff0c;跟踪一线游资和机构资金动向&#xff0c;识别短期热点和强势个股。 一.市场情绪 三大指数昨日集体调整&#xff0c;沪指午后跌超1%&#xff0c;深成指、创业板指盘中跌超2%&#xff0c;尾盘跌…
阅读更多...
【机器学习】数学基础详解

【机器学习】数学基础详解

线性代数&#xff1a;构建数据的骨架 数学对象 标量&#xff08;Scalar&#xff09; 标量是最基本的数学对象&#xff0c;代表了单个的数值&#xff0c;无论是整数还是实数。在机器学习中&#xff0c;标量可以用来表示一个模型的单个参数&#xff0c;如偏差&#xff08;bias&…
阅读更多...
appium driver install uiautomator2 安装失败

appium driver install uiautomator2 安装失败

报错 Installing ‘uiautomator2’ using NPM install spec ‘appium-uiautomator2-driver’ Error: Encountered an error when installing package: npm command ‘install --save-dev --no-progress --no-audit --omitpeer --save-exact --global-style --no-package-lock…
阅读更多...
深度学习之使用BP神经网络识别MNIST数据集

深度学习之使用BP神经网络识别MNIST数据集

目录 补充知识点 torch.nn.LogSoftmax() torchvision.transforms transforms.Compose transforms.ToTensor transforms.Normalize(mean, std) torchvision.datasets MNIST&#xff08;手写数字数据集&#xff09; torch.utils.data.DataLoader torch.nn.NLLLoss() to…
阅读更多...
LVM逻辑卷管理器

LVM逻辑卷管理器

LVM是Linux系统对硬盘分区进行管理的一种机制&#xff0c;在硬盘分区和文件系统之间添加了一个逻辑层&#xff0c;它提供了一个抽象的卷组&#xff0c;可以把多块硬盘进行卷组合并。这样&#xff0c;用户无需关心物理硬盘设备的底层架构和布局&#xff0c;就可以实现对硬盘分区…
阅读更多...
智过网：注册安全工程师注册有效期与周期解析

智过网：注册安全工程师注册有效期与周期解析

在职业领域&#xff0c;各种专业资格认证不仅是对从业者专业能力的认可&#xff0c;也是保障行业安全、规范发展的重要手段。其中&#xff0c;注册安全工程师证书在安全生产领域具有举足轻重的地位。那么&#xff0c;注册安全工程师的注册有效期是多久呢&#xff1f;又是几年一…
阅读更多...
Unity 九宫格

Unity 九宫格

1. 把图片拖拽进资源文件夹 2.选中图片&#xff0c;然后设置图片 3.设置九宫格 4.使用图片&#xff0c;在界面上创建2个相同的Image,然后使用图片&#xff0c;修改Image Type 为Sliced
阅读更多...
图书推荐：《和AI一起编程》

图书推荐：《和AI一起编程》

《Coding with AI For Dummies》这本书由Chris Minnick撰写&#xff0c;主要分为四个部分&#xff0c;涵盖了与AI相结合的编程技术、AI编码工具的应用、利用AI编写代码的具体实践&#xff0c;以及测试、文档编制和维护代码的相关内容。 克里斯明尼克(Chris Minnick)&#xff1a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023