题目1 300 最长递增子序列
题目链接 300 最长递增子序列
题意
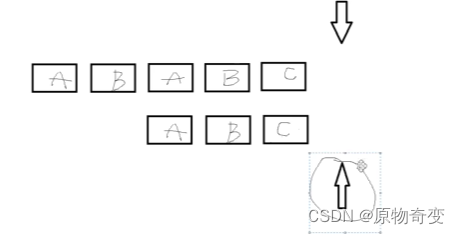
找到整数数组nums的最长严格递增子序列的长度(子序列并不改变原始的顺序,但是可以删除元素)
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i] 表示以nums[i]为结尾的最长递增子序列的长度
2)dp数组初始化
根据定义 长度至少是1 dp[i] = 1
3)递推公式
j从0到i-1各个位置的最长升序子序列 + 1 的最大值
要计算每个当前值dp[i]与现在遍历的nums[j]的长度的大小关系 每一个值都要进行比较
if(nums[i] > nums[j]) dp[i] = max(dp[j]+1,dp[i])
4)遍历顺序
根据递推公式 当前长度依赖于之前的结果 i从小到大遍历 j的遍历顺序无所谓,只要把i-1的范围内的值遍历完就ok
for(i=1;i<nums.size(); i++){
for(j=0;j<i;j++){
}
}
5)打印dp数组
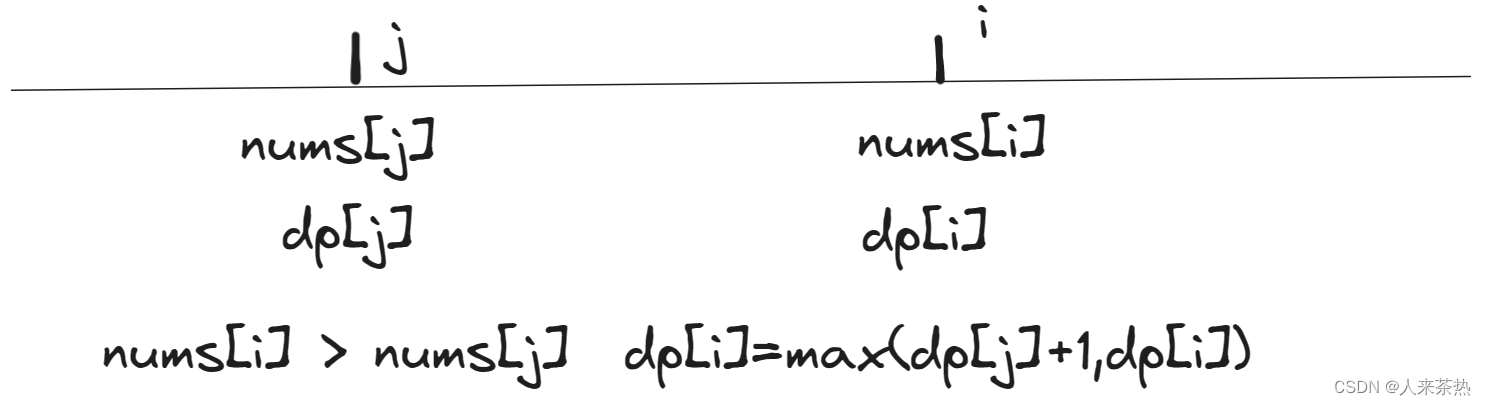
代码
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
//定义dp数组 初始化
vector<int> dp(nums.size(), 1);
int result = 0;
for(int i = 0; i < nums.size(); i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]) dp[i] = max(dp[j] + 1, dp[i]);
}
result = max(result, dp[i]);
}
return result;
}
};- 时间复杂度: O(n^2)
- 空间复杂度: O(n)
题目2 674 最长连续递增子序列
题目链接 674 最长连续递增序列
题意
找到未排序的整数数组的最长且连续递增的子序列的长度(不能删减元素了)
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i] 表示以nums[i]为结尾的最长连续递增子序列的长度
2)dp数组初始化
至少包含1个元素 dp[i] = 1
3)递推公式
只比较nums[i]与nums[i-1]即可,这样才可以保证是连续
不用去比较nums[j]与nums[i] (j是在0到i之间遍历)
if(nums[i] > nums[i-1]) dp[i] = dp[i-1] + 1
4)遍历顺序
根据递推公式 dp[i]依赖于dp[i-1] 从前往后推导
5)打印dp数组
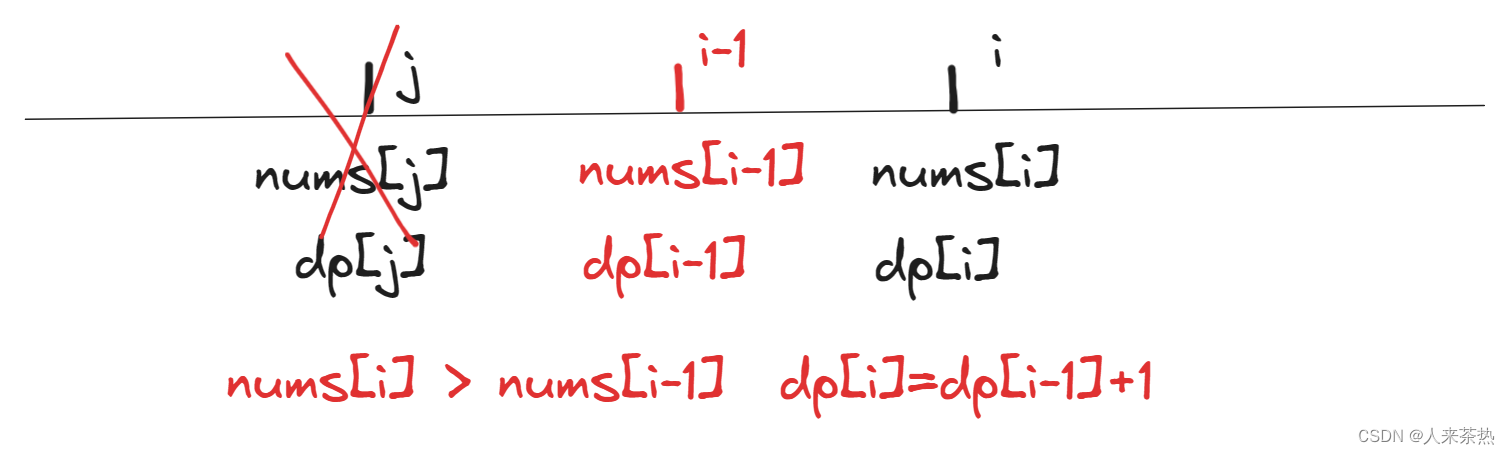
代码
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
//定义dp数组 初始化
vector<int> dp(nums.size(), 1);
int result = 1; //对于只有1个元素的数组
for(int i = 1; i < nums.size(); i++){
if(nums[i] > nums[i-1]) dp[i] = dp[i-1] + 1;
result = max(result, dp[i]);
}
return result;
}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
题目3 718 最长重复子数组
题目链接 718 最长重复子数组
题意
返回两个整数数组nums1和nums2的公共的最长子数组的长度
动态规划
动规五部曲
1)dp数组及下标i的含义
想到使用二维dp数组可以记录两个字符串的所有比较情况
dp[i][j] 表示以nums1[i-1]结尾的数组和以nums2[j-1]结尾的数组的公共最长子数组的长度
2)dp数组初始化
根据递推公式 初始化第一行第一列
根据dp数组定义 dp[i][0] 与 dp[0][j] 没有意义
根据递推公式 是在上一个基础上加1 应该从0开始往上加 dp[i-1][0] = 0 dp[0][j-1] = 0 其他下标可初始为任意值
3)递推公式
根据dp数组的定义 dp[i][j]以nums1[i-1]结尾 nums2[j-1]结尾 所以比较nums1[i-1]与nums2[j-1]
if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1
4)遍历顺序
遍历2个数组的顺序谁先谁后均可 只要把两个数组遍历完即可
之所以有等号,根据dp数组的定义 dp[i][j]以nums1[i-1]结尾 nums2[j-1]结尾
等号代表 nums1[nums1.size()-1] nums2[nums2.size()-1]
for(i=1;i<=nums1.size();i++){
for(j=1;j<=nums2.size();j++){
}
}
5)打印dp数组

代码
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
//定义dp数组 初始化dp数组
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
int result = 0;
for(int i = 1; i <= nums1.size(); i++){
for(int j = 1; j <= nums2.size(); j++){
if(nums1[i-1] == nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}
result = max(result, dp[i][j]);
}
}
return result;
}
};- 时间复杂度:O(n × m),n 为nums1长度,m为nums2长度
- 空间复杂度:O(n × m)