本文为离散数据与组合数学电子科技大学王丽杰老师的课程笔记，详细视频参考
【电子科技大学】离散数学（上） 王丽杰
【电子科技大学】离散数学（下） 王丽杰
latex的离散数学写法参考： 离散数学与组合数学-01

离散数学公式
!符号 代码 含义
$\wedge$ \wedge 且
$\vee$ \vee 或
$\cap$ \cap 交
$\cup$ \cup 并
$\subseteq$ \subseteq 子集
$⊈$ \nsubseteq 不是子集
$\subset$ \subset 真子集
$\not\subset$ \not\subset 不是真子集
$\in$ \in 属于
$\notin$ \not\in 不属于
$\leftrightarrow$ \leftrightarrow 等价
$\iff$ \Leftrightarrow 等值
$\neg$ \neg或\lnot 非
$\mathbb{R}$ \mathbb{R} 实数集
$\mathbb{Z}$ \mathbb{Z} 整数集
$\varnothing$ \varnothing 空集
$\forall$ \forall 对任意的
$\exists$ \exists 存在
$\ge$ \geq大于等于
$\le$ \leq 小于等于

$R/$ R\mkern-10.5mu/ 数值越大，斜杆越往字母左侧移动

离散数学与组合数学-02二元关系上

2.1 序偶和笛卡尔积

2.1.1 有序组的定义

2.1.2 笛卡儿积

笛卡儿积的性质

由笛卡儿积定义可以看出:
1 设 A, B 是任意两个集合，则不一定有 A × B = B × A，即笛卡儿积不满足交换律；
2 A × B = ∅ 当且仅当 A = ∅ 或者 B = ∅；
3 设 A,B, C 是任意三个集合，则不一定有 A × (B × C) = (A × B) × C，即笛卡儿积不满足结合律；
4 当集合 A, B 都是有限集时，|A × B| = |B × A| = |A| × |B|。
5 笛卡儿积对并运算和交运算满足分配律。

2.2 关系的定义

2.2.1 二元关系定义与案例

设 A, B 为两个非空集合，称A × B 的任意子集 R 为从 A 到 B 的一个二元关系，简称关系 (relation)。其中，
A 称为关系 R 的前域，
B 称为关系 R 的后域。
如果A = B，则称 R为A 上的一个二元关系。
案例:

1.令 A 为某大学所有学生的集合，B 表示该大学开设的所有课程的集合，则 A × B 可表示该校学生选课的所有可能情况。而真正的选课情况（即选课关系）则会是 A × B 的某一个子集。
2 令 F 为某地所有父亲的集合，S 表示该地所有儿子的集合，则 F × S 可表示父子关系的所有可能情况。 而真正的父子关系则会是 F × S 的某一个子集。

2.2.2 二元关系的数学符号

定义

1 若序偶 $<x,y>\in R$，通常把这一事实记为 xRy，读作“x 对 y 有关系 R”；
2 若序偶 $<x,y>\notin R$，通常把这一事实记为 $xR/y$，读作“x 对 y 没有关系 R”。

案例

设 $R_1$ 为自然数集合上的小于关系，则 $<2,3>\notin R_1(或2R_{1}3)，$但$<5,5>\notin R1$(或$5R/5$)；
2 设 $R_2$ 为中国城市的地区归属关系，则 $成都R_2四川$，但 $重庆R/四川$.

枚举二元关系

2.2.3 定义域和值域

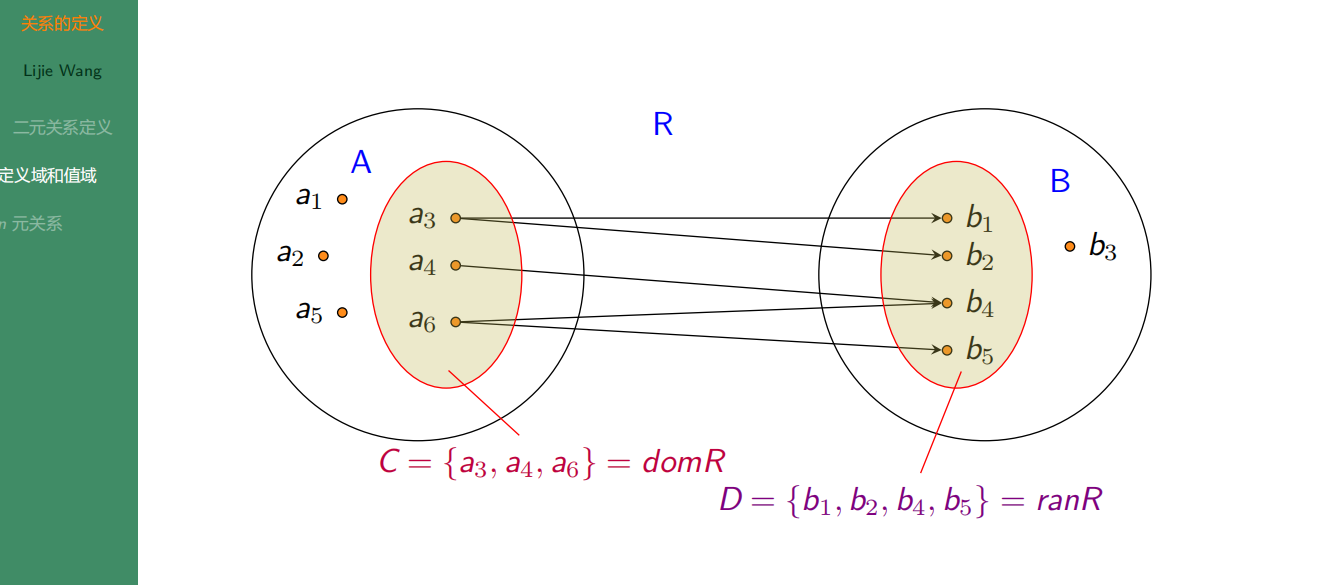
2.2.4 二元关系概念的推广

2.3 关系的表示

2.3.1 集合表示法

2.3.2 图形表示关系

2.3.3 关系矩阵表示法

2.3.4 布尔矩阵运算

布尔矩阵的并和交运算

案例：

布尔矩阵的积运算

2.4 关系的运算

2.4.1 关系的并交差补运算

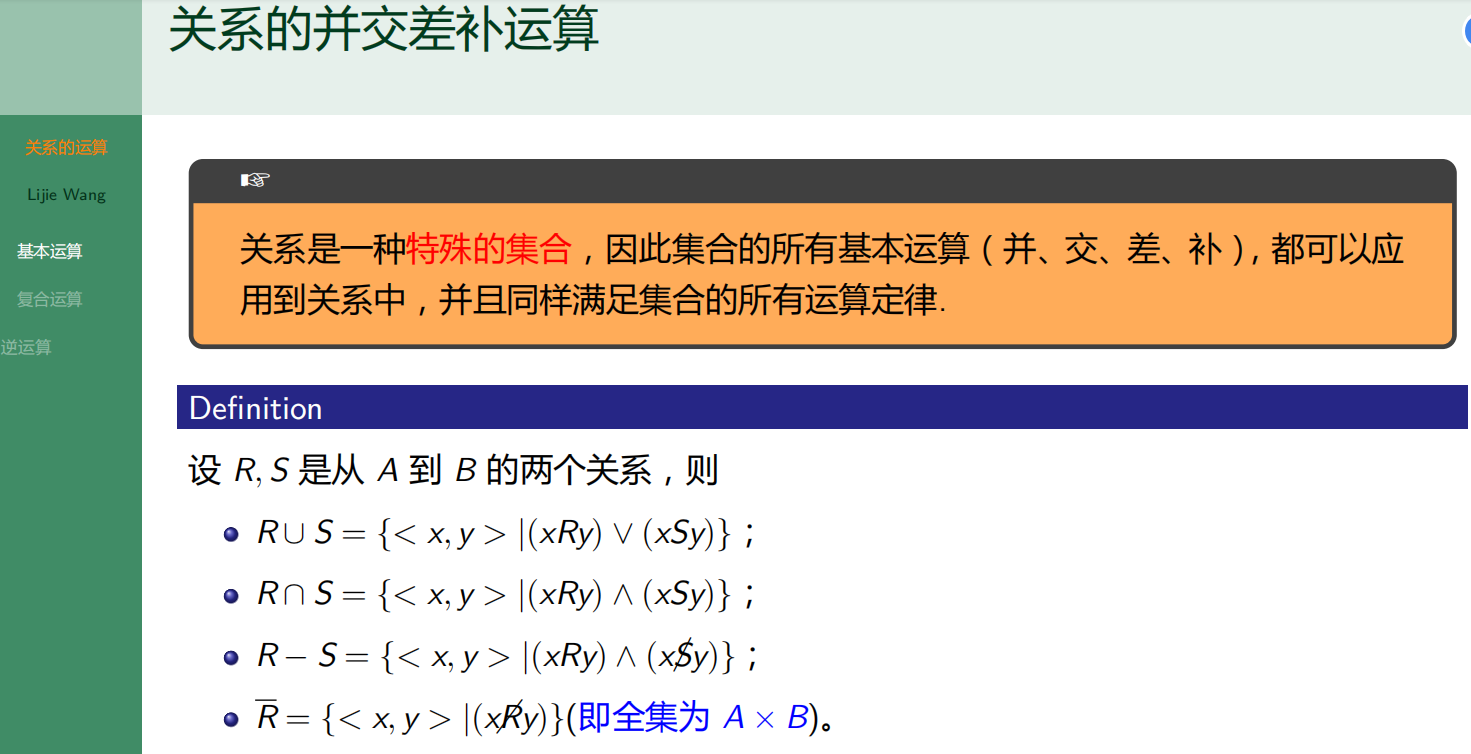
2.4.2 关系的复合运算

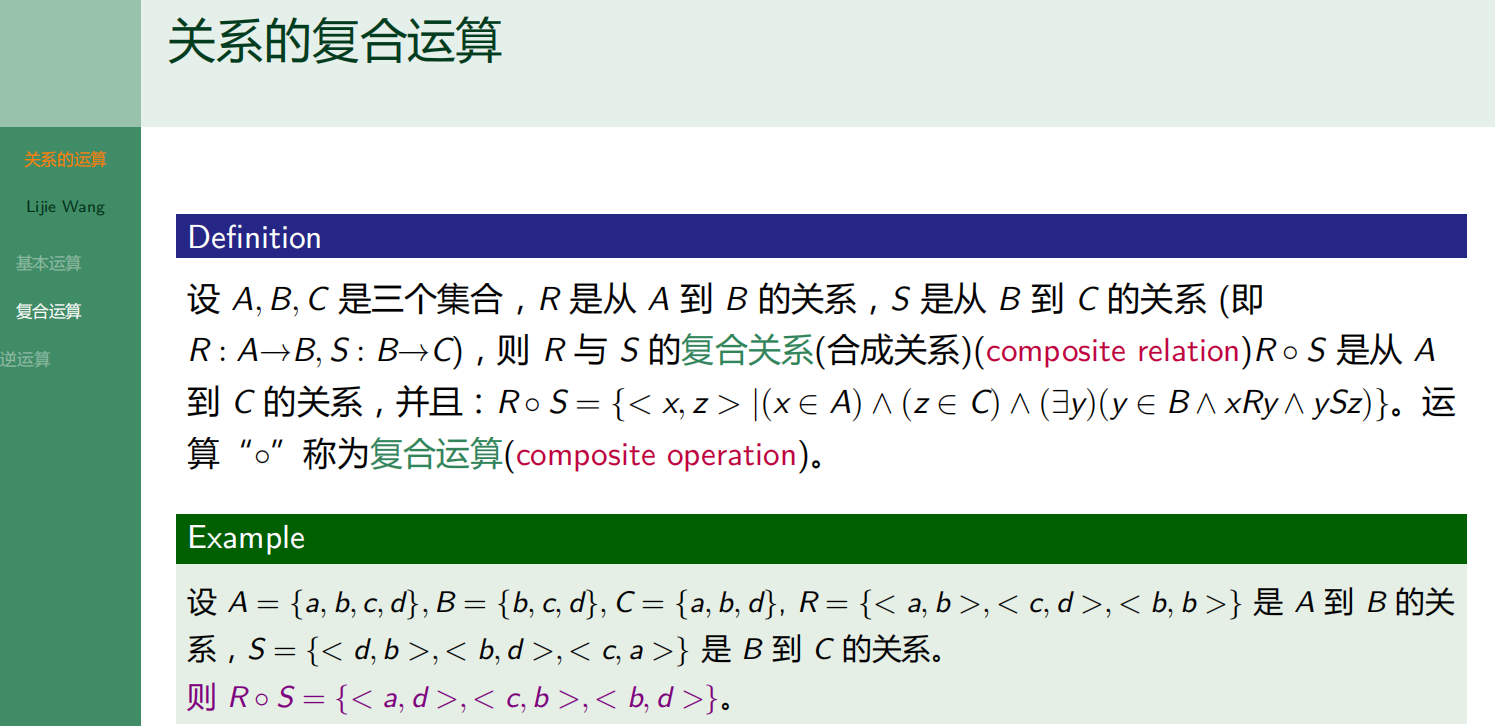
关系图和关系矩阵进行符合运算

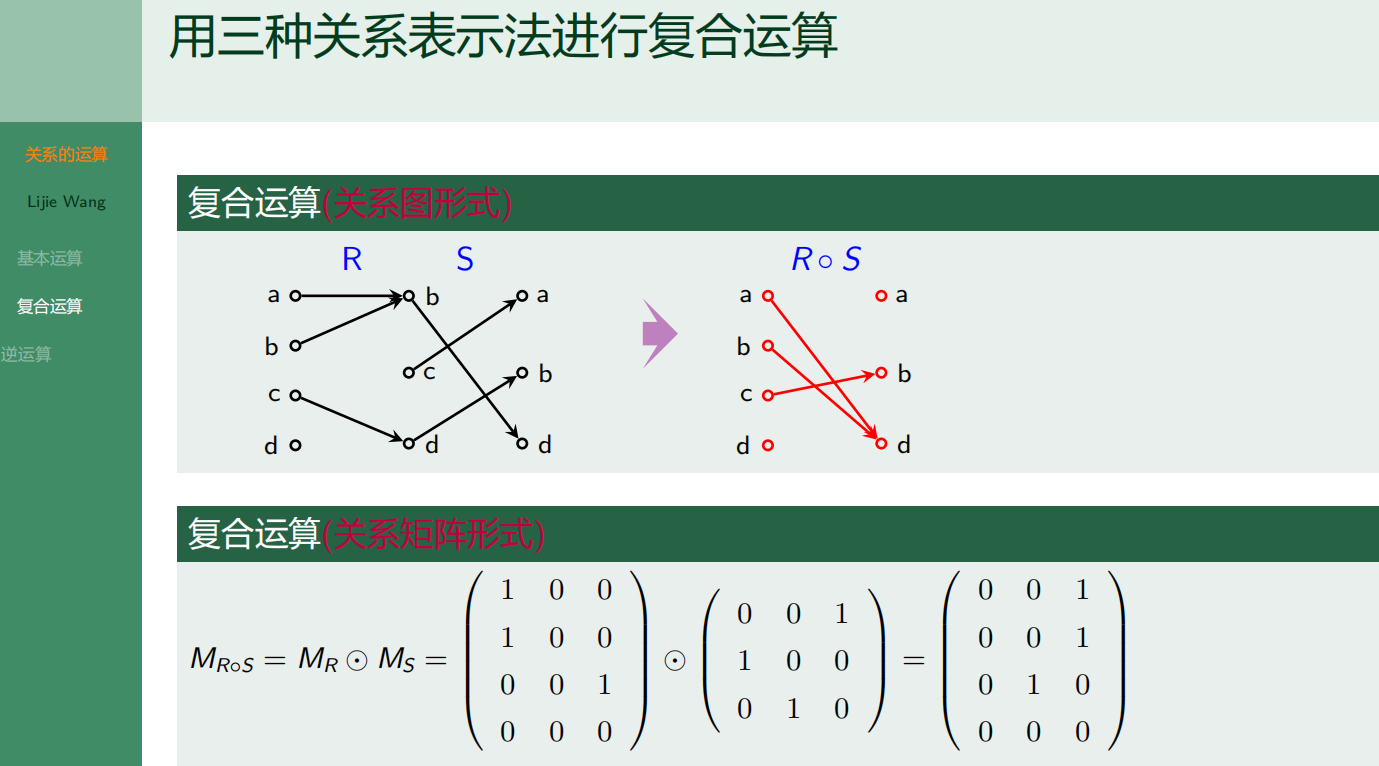
2.4.3 关系的逆运算

2.5关系的运算性质

2.5.1 复合预算性质

结合律和同一律

分配率

2.5.2 逆运算性质定律

2.6关系的幂运算

~~未完待续~~
见系列博客下

2.7关系的性质1

~~未完待续~~
见系列博客下

2.8关系的性质2

~~未完待续~~
见系列博客下

2.9关系的闭包

~~未完待续~~
见系列博客下

2.10 等价关系

~~未完待续~~
见系列博客下

2.11 次序关系

~~未完待续~~
见系列博客下