题目描述

原题链接：222. 完全二叉树的节点个数

解题思路

1、普通二叉树节点个数求法

（1）迭代：层序遍历BFS

遍历一层获取一层结点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(!root)       return 0;
        int res = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int n = que.size();
            while(n--) {
                TreeNode* node = que.front();
                que.pop();
                res++;
                if(node->left)      que.push(node->left);
                if(node->right)     que.push(node->right);
            }
        }
        return res;
    }
};

时间复杂度 $O(n)$
空间复杂度 $O(n)$

（2）递归：先序遍历DFS

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int nums = 0;
    int countNodes(TreeNode* root) {
        if(!root)       return 0;
        nums++;                             // 中：每遍历一个非空结点，加一
        if(!root->left && !root->right)     return 1;    // 刚开始遍历时，树中若只有一个结点，则返回1
        countNodes(root->left);             // 左
        countNodes(root->right);            // 右
        return nums;    // 最后从栈一个弹出的函数，有nums的最终值
    }
};

时间复杂度 $O(n)$
空间复杂度 $O(logn)$ （不考虑系统栈）

（3）迭代：后序遍历（子问题分解）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(!root)       return 0;
        int leftcnt = countNodes(root->left);       // 左
        int rightcnt = countNodes(root->right);     // 右
        return leftcnt + rightcnt + 1;              // 中：将结果返回给上一层
    }
};

时间复杂度 $O(n)$
空间复杂度 $O(logn)$ （不考虑系统栈）

2、完全二叉树性质求节点个数

满二叉树的特点：左子树左侧边的高度=右子树右侧边的高度，节点个数=$2^n-1$。
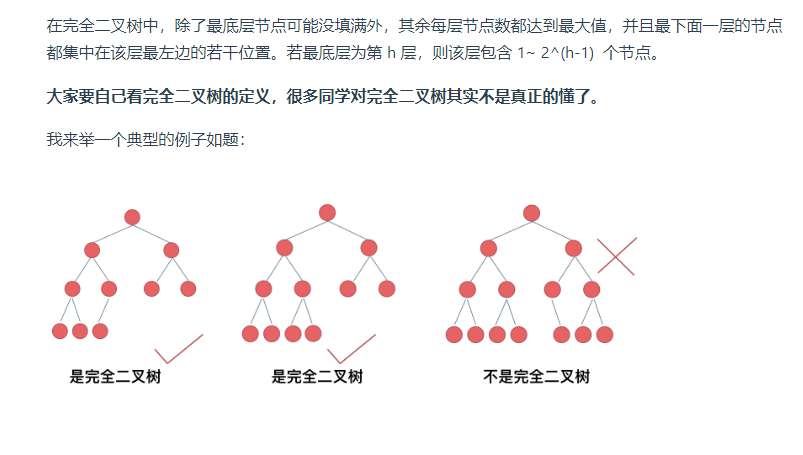
完全二叉树的特点：除了最后一层外，其余层全部为满二叉树。

可以将这个问题分解成子问题，求根节点所拥有的左右子树节点个的结点个数，最后得到整棵树的总个数。而每遍历到一颗子树时，可以利用满二叉树的特点查看该子树是否为一颗满二叉树，若为满二叉树，直接根据节点个数公式返回即可，若为不满二叉树，则算上该节点（总结点个数加一），然后再向下递归计算其左右子树结点个数。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int level = 0;
    int countNodes(TreeNode* root) {
        if(!root)       return 0;        
        // 先求左子树左侧高度和右子树右侧高度
        TreeNode* leftnode = root->left;
        TreeNode* rightnode = root->right;
        int leftLevel = 0, rightLevel = 0;      // 2左移从0开始，1左移从1开始
        while(leftnode) {
            leftLevel++;
            leftnode = leftnode->left;            
        }
        while(rightnode) {
            rightLevel++;
            rightnode = rightnode->right;
        }
        // 若为满二叉树，左子树左侧高度应该等于右子树右侧高度
        if(leftLevel == rightLevel)      return (1 << leftLevel) - 1;       // 2<<0 = 2 , 2<<n = 2^(n+1)，因此规定从0开始
        // 若不为满二叉树，则算此结点个数，并求再求左右子树的结点个数
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

时间复杂度 $O(lo{g}^{2}n)$
空间复杂度 $O(logn)$

注：$0<n\le 4$时，$O(n)\ge O(lo{g}^{2}n)$；当$n\ge 5$时，$O(n)＜O(lo{g}^{2}n)$

参考文章：222.完全二叉树的节点个数、如何计算完全二叉树的节点数