循环神经网络RNN和长短期记忆神经网络LSTM

欢迎访问Blog总目录！

1.循环神经网络RNN（Recurrent Neural Network）

1.1.学习链接

一文看尽RNN（循环神经网络） - 知乎 (zhihu.com)

一文搞懂RNN（循环神经网络）基础篇 - 知乎 (zhihu.com)

1.2.RNN结构

循环神经网络（Recurrent Neural Network, RNN）是一类以 序列（sequence）数据为输入，在序列的演进方向进行 递归（recursion）且所有节点（循环单元）按链式连接的 递归神经网络（recursive neural network）。

RNN的输入不仅与当前时刻的输入有关，还与之前时刻的状态（输出）有关。（记忆功能）

RNN的基本结构：

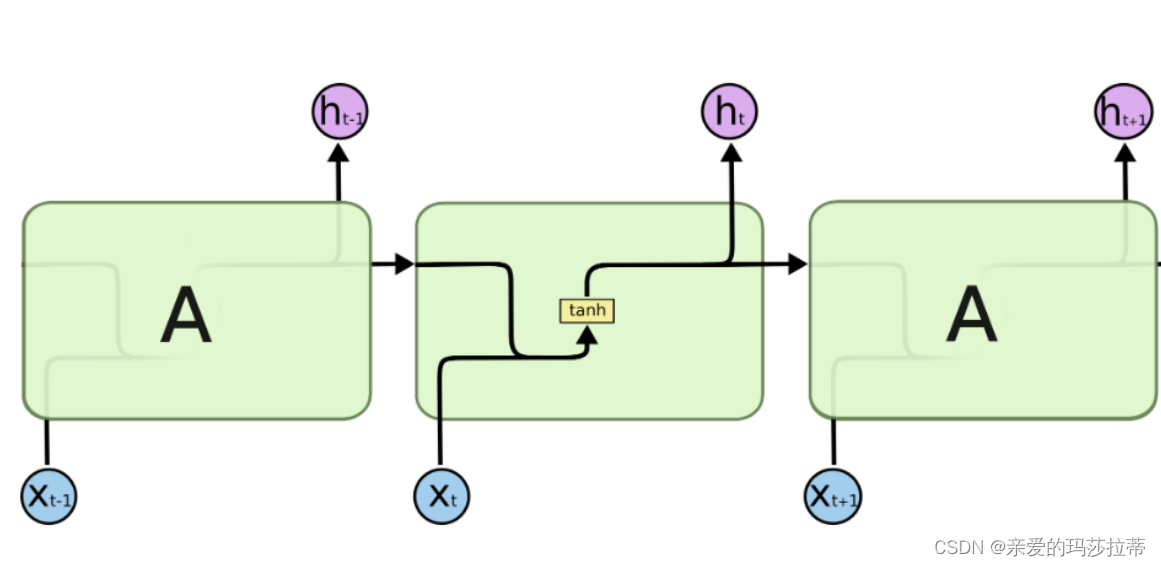
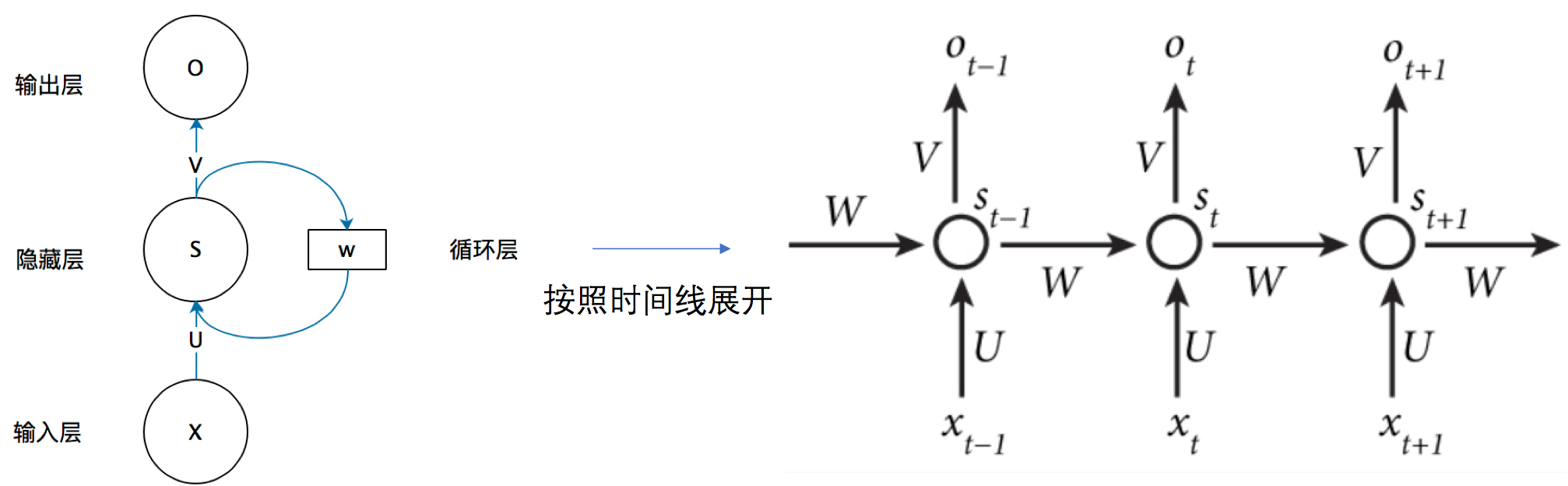
RNN结构公式：
$$\begin{gathered} O_t=g(V\cdot S_t) \\ {S}_t=f(U\cdot X_t+W\cdot S_{t-1}) \end{gathered}$$

1.3.RNN缺点

梯度弥散：在误差反向传播上，误差会逐级*W，当W小于1时，误差在传递过程中会越来越小。到第一级时，误差会趋近于0，这会影响神经网络的训练修正。这种现象为梯度弥散。

梯度爆炸：在误差反向传播上，误差会逐级*W，当W大于1时，误差在传递过程中会越来越大。到第一级时，误差会非常大，这会影响神经网络的训练修正。这种现象为梯度爆炸。这也是RNN无法回忆久远记忆的原因。

长期依赖问题：由于只能回忆起$S_{t-1}$，所以RNN只能处理比较接近的上下文信息。

2.长短期记忆递归神经网络LSTM（Long Short Term Memory）

2.1学习链接

LSTM - 长短期记忆递归神经网络 - 知乎 (zhihu.com)

简单理解LSTM神经网络-CSDN博客

Understanding LSTM Networks – colah’s blog

2.2.LSTM结构

LSTM有效解决了RNN的梯度问题和长期依赖问题。使用LSTM可以有效地、有选择地传递和表达长时间序列中的信息并且不会导致长时间前的有用信息被忽略（遗忘）。

【直观理解】LSTM相较于RNN，多了输入控制器、输出控制器和忘记控制器，以及全局记忆。假设全局记忆为故事主线，原本的RNN体系为直线剧情。如果分线剧情对主线剧情非常重要，输入控制器就会将该分线剧情写入主线。如果分线剧情对主线剧情有影响，忘记控制器会忘记之前的部分主线剧情，按比例替换成现在的新剧情。故主线剧情的更新取决于输入和忘记控制器。

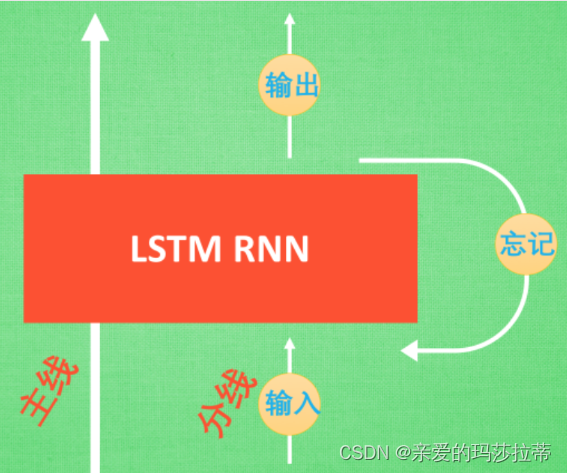
2.2.1.基本结构

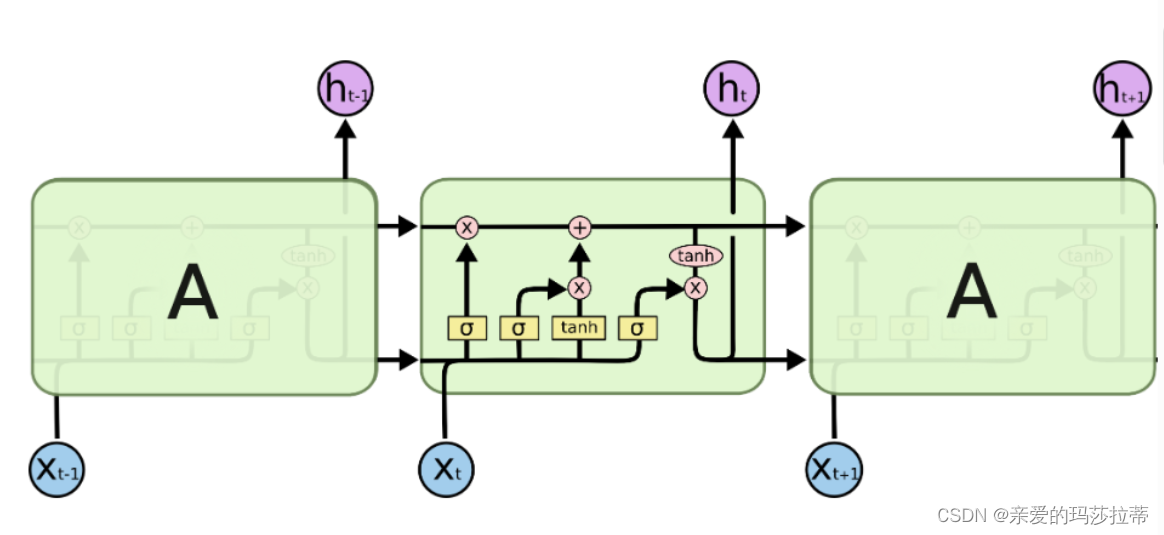
2.2.1.1.隐藏态（单元状态）

隐藏态即为主线，递归神经网络对于输入数据的“记忆”，用$C_t$表示神经元在$t$时刻过后的“记忆”，这个向量涵盖了在$t+1$ 时刻前神经网络对于所有输入信息的“概括总结”。

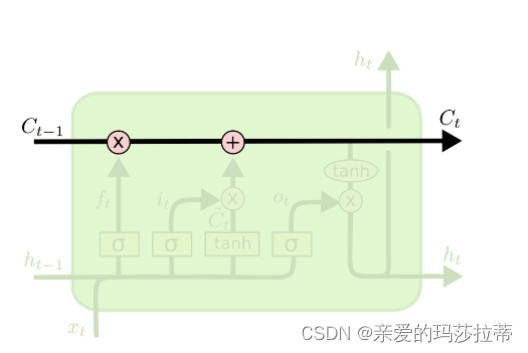
2.2.1.2.遗忘门

$\sigma$为sigmoid神经层，sigmoid 函数会将任意输入压缩到 (0,1) 的区间上。遗忘门输入新的输入和上一时刻的输出，通过sigmoid 函数后，如果向量某个分量在通过sigmoid层后变为0，那么显然单元状态在对位相乘后对应的分量也会变成0，即“遗忘”了这个分量上的信息；如果向量某个分量在通过sigmoid层后变为1，即单元状态会“保留完整记忆”。遗忘门输出为（0,1）。

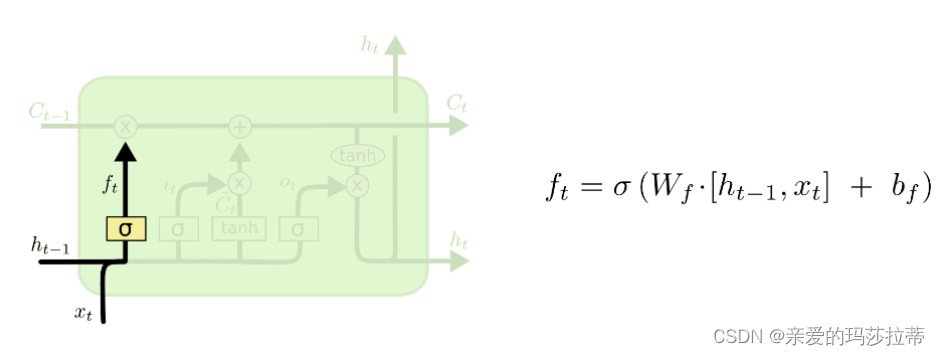
2.2.1.3.记忆门

tanh层将任意输入压缩到（-1，1）的区间上。首先，用tanh层将现在的输入向量中的有效信息提取出来，然后使用左侧的sigmoid函数来控制这些记忆要放“多少”进入单元状态。

在选择信息后，需要将信息并入“主线”单元状态中。

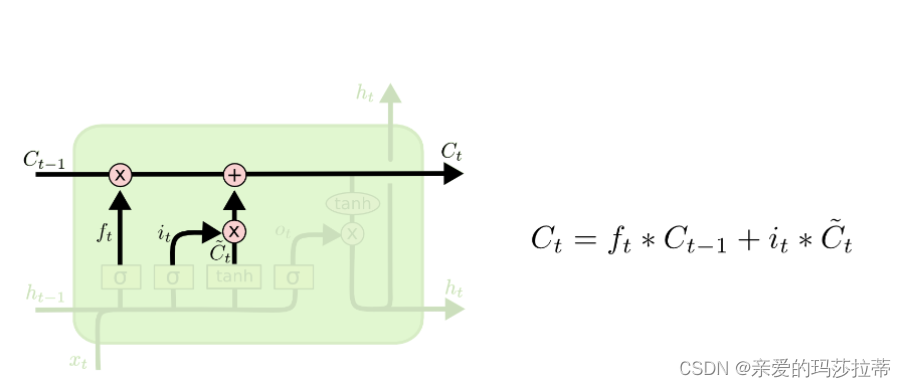
2.2.1.4.输出门

模型的输出，首先是通过sigmoid层来得到一个初始输出，然后使用tanh将值缩放到-1到1间（对先前信息的压缩处理），再与sigmoid得到的输出逐对相乘，从而得到模型的输出$h_t$。

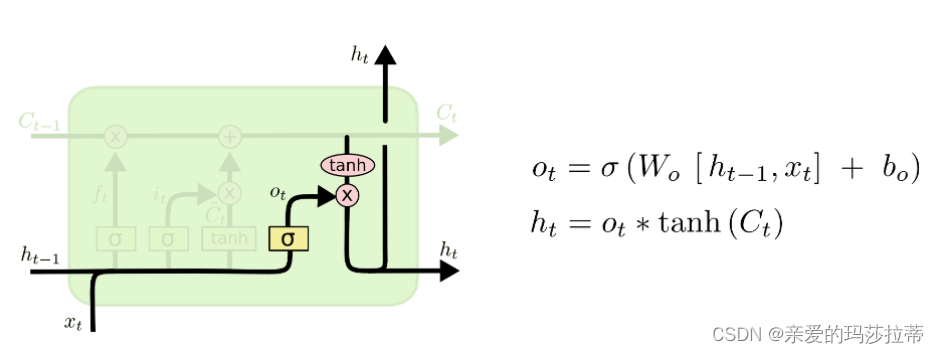
2.2.2.核心要素

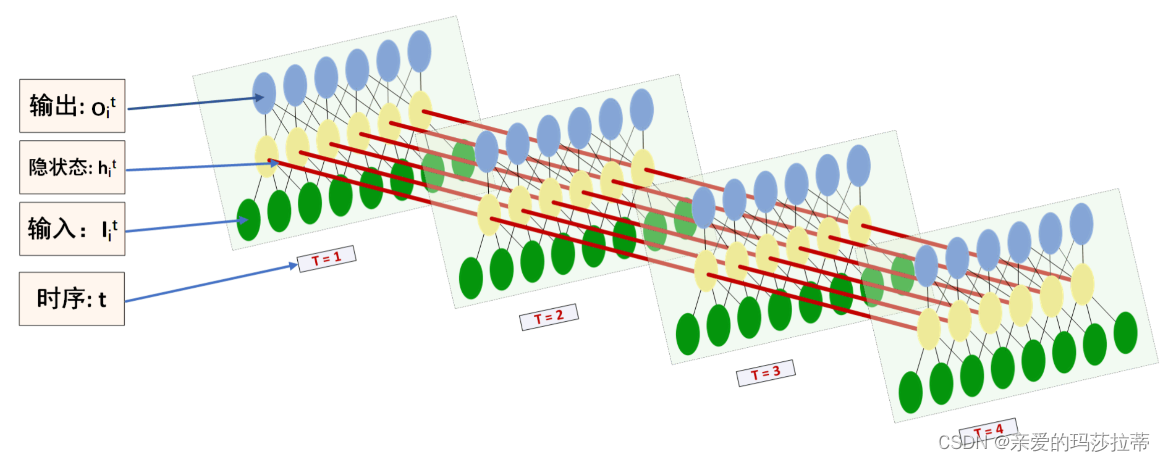
名称	name	含义
时间长度	Time_step	是指输入x数据的时间长度，对应$x_1,x_2,...,x_T$
输入尺寸	input_size	是指输入x数据的数据大小。
隐藏层尺寸	hidden_size	是指隐藏层输出数据h的数据大小。 注意：网络输出数据的大小=隐藏层数据大小。

2.3.pytorch LSTM

2.3.1.API

API:LSTM — PyTorch 2.2 documentation

class RNNBase(Module):
	...
    def __init__(self, mode, input_size, hidden_size,
                 num_layers=1, bias=True, batch_first=False,
                 dropout=0., bidirectional=False):

参数	含义
input_size	输入$x_t$数据的数据大小
hidden_size	隐藏层的大小（即隐藏层节点数量），输出向量h和output的维度等于隐藏节点数
num_layers	LSTM块的级联数量（非时间尺度上的）
batch_first	默认为False，也就是说官方不推荐我们把batch放在第一维，此时输入输出的各个维度含义为 (seq_length,batch,feature)，True即为放在第一位

输入数据： input, (h_0,c_0)

参数	含义	维度
input	输入数据$x_t$	(time_step, batch, input_size) time_step为序列时间长度； input_size为单个时刻的数据长度
h_0	隐藏层输出	(num_layers * num_directions, batch, hidden_size)|如果LSTM为双向（单向），则num_directions=2（1）
c_0		(num_layers * num_directions, batch, hidden_size)

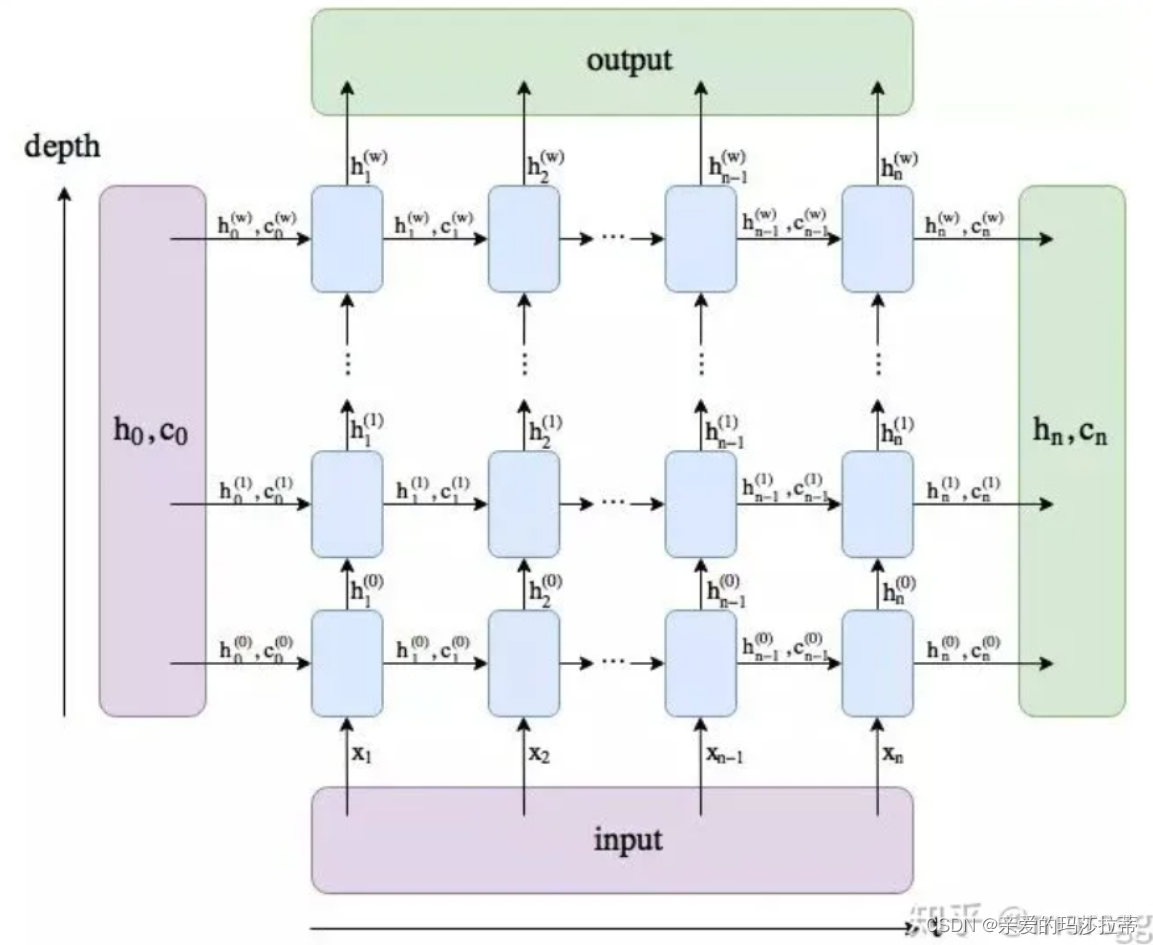
输出数据： output，(h_n, c_n)

参数	含义	维度
output	输出数据$x_t$	(time_step, batch, num_directions * hidden_size)
h_T	最后一个time_step的隐藏层输出	(num_layers * num_directions, batch, hidden_size)
c_T	最后一个time_step的cell输出	(num_layers * num_directions, batch, hidden_size)

2.3.2.LSTM的搭建

案例：使用$sint$预测$cost$的取值

class Lstm(nn.Module):
    def __init__(self):
        super(Lstm, self).__init__()

        self.lstm = nn.LSTM(
            input_size=INPUT_SIZE,  # 1 数据长度为1
            hidden_size=32,  # rnn hidden unit 隐藏层节点数
            num_layers=1,  # number of rnn layer
            batch_first=True,  # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
        )
        self.out = nn.Linear(32, 1)

    def forward(self, x, h_state):
        # x (batch, time_step, input_size)
        # h_state (n_layers, batch, hidden_size)
        # r_out (batch, time_step, hidden_size)
        r_out, h_state = self.lstm(x, h_state)

        outs = []  # save all predictions
        for time_step in range(r_out.size(1)):  # calculate output for each time step
            outs.append(self.out(r_out[:, time_step, :]))
        return torch.stack(outs, dim=1), h_state

rnn = Lstm()
print(rnn)
'''
Lstm(
  (lstm): LSTM(1, 32, batch_first=True)
  (out): Linear(in_features=32, out_features=1, bias=True)
)'''

2.3.3.示意图⭐️