题目描述：

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

解题思路一：回溯。回溯三部曲

1. 递归函数参数
   首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示:

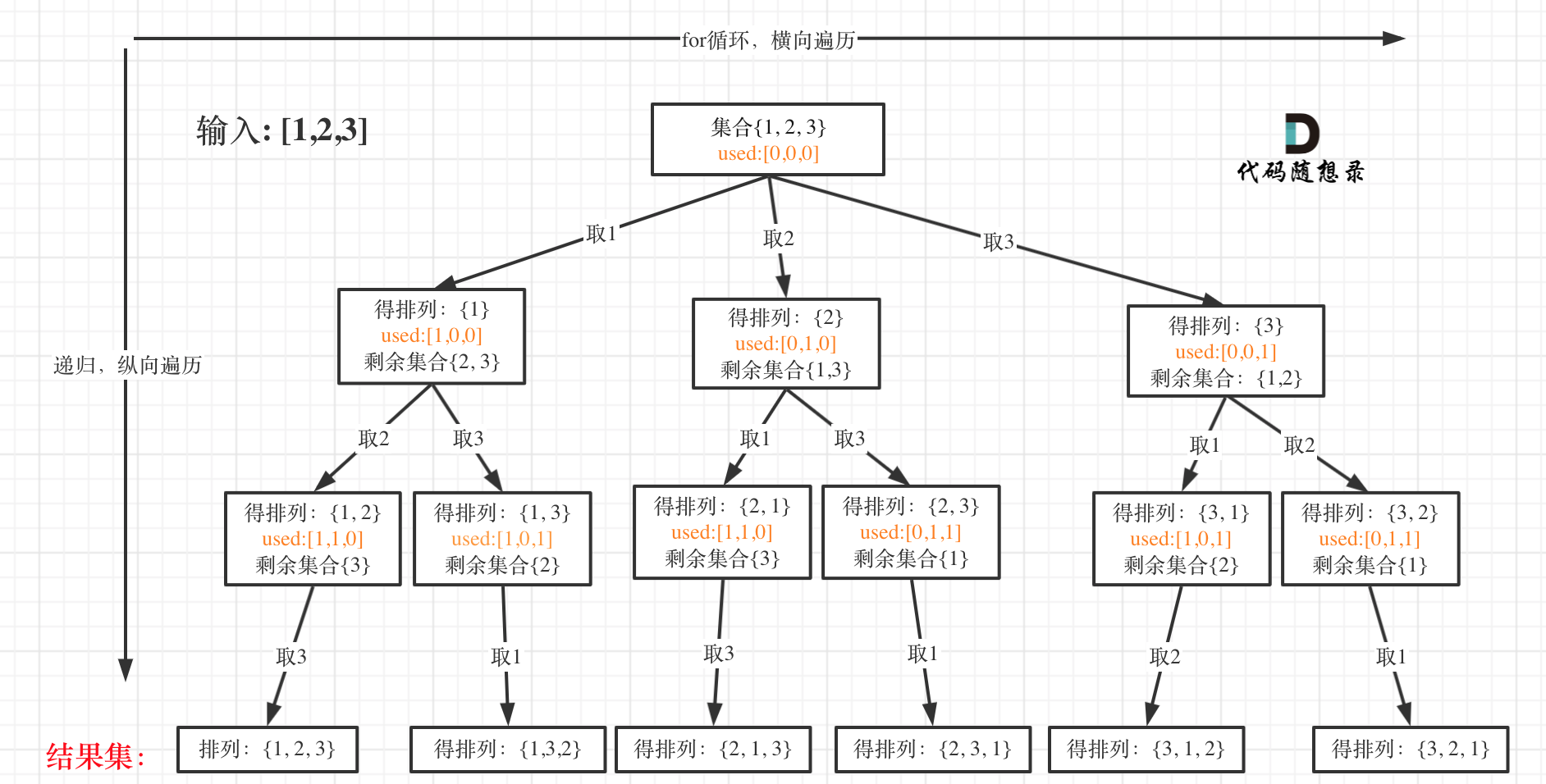
2. 递归终止条件
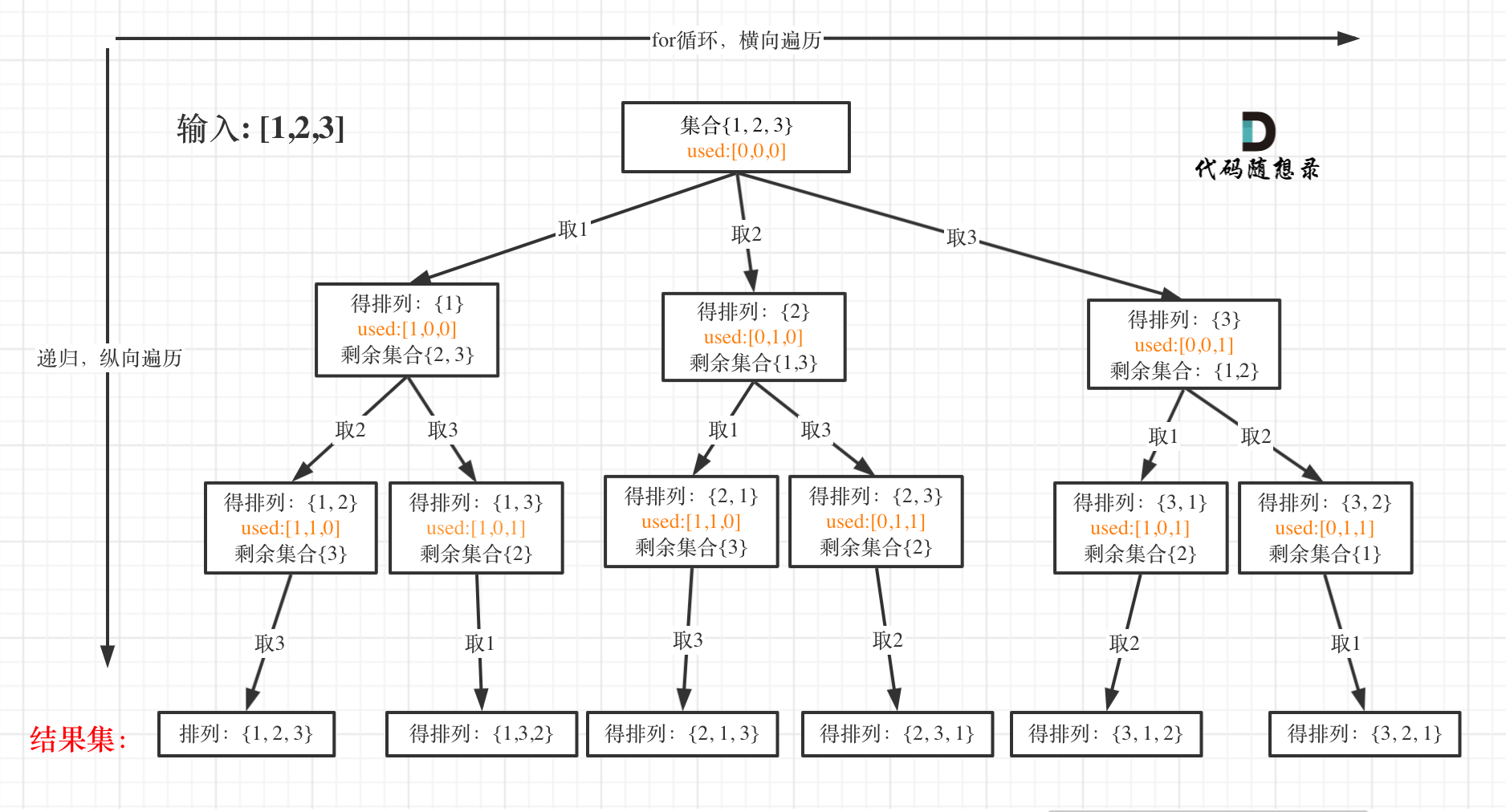可以看出叶子节点，就是收割结果的地方。

那么什么时候，算是到达叶子节点呢？

当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。
3. 单层搜索的逻辑
这里和77.组合问题 (opens new window)、131.切割问题 (opens new window)和78.子集问题 (opens new window)最大的不同就是for循环里不用startIndex了。

因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。

而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []
        self.backtracking(nums, [False] * len(nums), [], res)
        return res

    def backtracking(self, nums, used, path, res):
        if len(path) == len(nums):
            res.append(path[:])
            return
        for i in range(len(nums)):
            if used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, used, path, res)
            used[i] = False
            path.pop()

时间复杂度：O(n×n!)
空间复杂度：O(n)

解题思路二：0

时间复杂度：O(n)
空间复杂度：O(n)

解题思路三：0

时间复杂度：O(n)
空间复杂度：O(n)