浮点数在内存中的存储
- 浮点数存储规则
- 小数点后数值的二进制转换
- float和double存储图示
- 优化存储方案
- E不全为0或不全为1
- E全为0
- E全为1
浮点数存储规则
大家都知道整型数据是以补码的方式存放在内存中。以下几个概念是需要知道的:
- 原码,补码,反码都是以二进制形式表示的。
- 正整数的原码,反码,补码都相同。
- 负整数的补码=反码+1=原码的符号位不变,数值位按位取反。
但是浮点数不同,浮点数有着一套自己的存储规则。
根据国际标准IEEE(电气和电子工程协会) 754,任意一个二进制浮点数V可以表示成下面的形式:
- (-1)^S * M * 2^E
- (-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。
- M表示有效数字,大于等于1,小于2。
- 2^E表示指数位。
- E是一个无符号整数。
小数点后数值的二进制转换
大家对于整数的二进制转换是了熟于心,但是往往会忽略了小数的二进制转换。
7.25
例如上面的十进制数字7.25,小数点前的7可以转换为:
4
+
2
+
1
=
2
2
+
2
1
+
2
0
=
111
4+2+1=2^{2}+2^{1}+2^{0}=111
4+2+1=22+21+20=111
小数点后的数值0.25转换为:
1
4
=
1
2
2
=
2
−
2
=
.
01
\frac{1}{4}=\frac{1}{2^{2}}=2^{-2}=.01
41=221=2−2=.01
所以:
7.25=111.01
所以按照规则,用float来存储7.25的话:7.25=111.01 = ( − 1 ) 0 ∗ 1.1101 ∗ ( 2 ) 2 (-1)^{0}*1.1101*(2)^{2} (−1)0∗1.1101∗(2)2
- S=0
- M = 1.1101
- E = 2
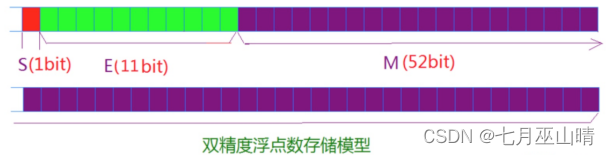
float和double存储图示
IEEE 754规定: 对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位为有效数字M。
对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。
优化存储方案
前面提到的规则是0<=M<=1。这就导致当浮点数不为0时,M一定是1.***这样的格式的,小数点前面一定会有一个1。每次都存储这个1显得冗余浪费空间。因此IEE 754规定存储在内存中时,去除掉小数点前的1,只将小数点后面的二进制数值存进去。
下面我们来看一种情况:
0.5的存储
(
0.5
)
10
(0.5)_{10}
(0.5)10=
(
0.1
)
2
(0.1)_{2}
(0.1)2 =
(
−
1
)
0
∗
1.0
∗
(
2
)
−
1
(-1)^{0}*1.0*(2)^{-1}
(−1)0∗1.0∗(2)−1
我们会发现一个特别的现象,E=-1,前面说过,E是一个无符号整数,那这个-1该怎么存储呢?
IEE 754规定:
存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
所以这里是float类型,E=-1,存储时加上127,也就是真正存入内存的是:-1+127=126。
另外E从内存中取出还有三种情况值得我们注意:
E不全为0或不全为1
这就是上面我们讨论的那种情况,
- 如果是float类型的,取出来的数直接减去127,就可得到E的真实值。
- 如果是double类型的,取出来的数直接减去1023,就可得到E的真实值。
E全为0
这个作为特殊对待,如果E全为0,说明真实值为-127,也就是这个数是一个
1
2
127
\frac{1}{2^{127}}
21271的,这已经是一个很小很小的数了,无限接近于0了。
因此,IEEE 754规定,
- 如果是float类型的,
E全为0时,E=1-127(可不是前面说的-127,那只是举例)。 - 如果是double类型的,
E全为0时,E=1-1023 - 既然此时数值无限接近0,那么M也就不需要再加上1,但是S依旧需要,用来标识±0。
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);