0. 简介
介绍计算机中数的表示方法,主要内容来自 c s a p p csapp csapp。
1. 整数的表示
包括有符号整数与无符号整数的表示。
假设
w
→
=
[
w
n
−
1
w
n
−
2
.
.
.
w
0
]
\overrightarrow w=[w_{n-1}w_{n-2}...w_0]
w=[wn−1wn−2...w0]
为一种整数。
1.1 无符号整数
计算机是二进制的,且数据长度固定。
所以无符号二进制数实际上直接表示即可。
B 2 U ( w → ) = ∑ i = 0 n − 1 w i × 2 i B2U(\overrightarrow w)=\sum_{i=0}^{n-1}w_i \times 2^{i} B2U(w)=i=0∑n−1wi×2i
1.2 有符号整数
-
补码编码
最高位来表示符号位
B 2 T ( w → ) = − w n − 1 ∗ 2 n − 1 + ∑ i = 0 n − 2 w i × 2 i B2T(\overrightarrow w)=-w_{n-1}*2^{n-1}+\sum_{i=0}^{n-2}w_i\times2^i B2T(w)=−wn−1∗2n−1+i=0∑n−2wi×2i
所以范围为有符号整数范围为 − 2 n − 1 ∼ 2 n − 1 − 1 -2^{n-1}\sim 2^{n-1}-1 −2n−1∼2n−1−1 -
反码编码
B 2 O ( w → ) = − w n − 1 ∗ ( 2 n − 1 − 1 ) + ∑ i = 0 n − 2 w i × 2 i B2O(\overrightarrow w)=-w_{n-1}*(2^{n-1}-1)+\sum_{i=0}^{n-2}w_i\times2^i B2O(w)=−wn−1∗(2n−1−1)+i=0∑n−2wi×2i -
原码编码
B 2 S ( w → ) = ( − 1 ) w n − 1 ⋅ ∑ i = 0 n − 2 w i × 2 i B2S(\overrightarrow w)=(-1)^{w_{n-1}} \cdot \sum_{i=0}^{n-2}w_i \times2^i B2S(w)=(−1)wn−1⋅i=0∑n−2wi×2i
为什么使用补码?原码和反码的表示中,对于 0 0 0的表示有歧义。 + 0 ( 0000 0000 ) +0(0000\ 0000) +0(0000 0000), − 0 ( 1000 0000 ) -0(1000\ 0000) −0(1000 0000)
1.3 有符号数与无符号数间转换
无符号数转有符号数
B
2
U
(
w
→
)
=
∑
i
=
0
n
−
1
w
i
×
2
i
=
w
n
−
1
∗
2
n
−
1
+
∑
i
=
0
n
−
2
w
i
×
2
i
B
2
T
(
w
→
)
=
−
w
n
−
1
∗
2
n
−
1
+
∑
i
=
0
n
−
2
w
i
×
2
i
\begin{align} B2U(\overrightarrow w)=\sum_{i=0}^{n-1}w_i \times 2^i=w_{n-1} *2^{n-1} +\sum_{i=0}^{n-2}w_i \times 2^i\\ B2T(\overrightarrow w)=-w_{n-1}*2^{n-1}+\sum_{i=0}^{n-2}w_i\times2^i \end{align}
B2U(w)=i=0∑n−1wi×2i=wn−1∗2n−1+i=0∑n−2wi×2iB2T(w)=−wn−1∗2n−1+i=0∑n−2wi×2i
(
2
)
−
(
1
)
(2)-(1)
(2)−(1)得到
B
2
T
(
w
→
)
−
B
2
U
(
w
→
)
=
−
w
n
−
1
∗
2
n
B2T(\overrightarrow w)-B2U(\overrightarrow w)=-w_{n-1} *2^{n}
B2T(w)−B2U(w)=−wn−1∗2n
所以
U
2
T
(
w
→
)
=
−
w
n
−
1
∗
2
n
+
B
2
U
(
w
→
)
U2T(\overrightarrow w)=-w_{n-1}*2^n+B2U(\overrightarrow w)
U2T(w)=−wn−1∗2n+B2U(w)
分类讨论下最高位情况
l
e
t
u
=
B
2
U
(
w
→
)
U
2
T
(
u
)
=
{
u
,
u
≤
T
M
a
x
n
(
w
n
−
1
=
1
)
u
−
2
n
,
u
>
T
M
a
x
n
let\ u=B2U(\overrightarrow{w})\\ \begin{equation} U2T(u )= \begin{cases} u,\quad u \le TMax_{n}(w_{n-1} =1)\\ u-2^n,\quad u \gt TMax_{n} \end{cases} \end{equation}
let u=B2U(w)U2T(u)={u,u≤TMaxn(wn−1=1)u−2n,u>TMaxn
同理可得有符号转无符号数
B
2
U
(
w
→
)
=
U
2
T
(
w
→
)
+
w
n
−
1
∗
2
n
B2U(\overrightarrow w)=U2T(\overrightarrow w)+w_{n-1}*2^n
B2U(w)=U2T(w)+wn−1∗2n
同样分类讨论最高位情况
l
e
t
t
=
U
2
T
(
w
→
)
T
2
U
(
t
)
=
{
t
,
t
≥
0
)
t
+
2
n
,
t
<
0
let\ t=U2T(\overrightarrow w)\\ \begin{equation} T2U(t)= \begin{cases} t,\quad t \ge 0)\\ t+2^n,\quad t \lt 0 \end{cases} \end{equation}
let t=U2T(w)T2U(t)={t,t≥0)t+2n,t<0
1.4 数位扩展
无符号数扩展,直接在前面添加 0 0 0即可。
u
→
=
[
u
n
−
1
u
n
−
2
⋯
u
0
]
u
′
→
=
[
0
⋯
u
n
−
1
⋯
u
0
]
\overrightarrow u=[u_{n-1}u_{n-2}\cdots u_0]\\ \overrightarrow {u'}= [0\cdots u_{n-1}\cdots u_0]
u=[un−1un−2⋯u0]u′=[0⋯un−1⋯u0]
根据
B
2
U
(
w
→
)
=
∑
i
=
0
n
−
1
w
i
×
2
i
B2U(\overrightarrow w)=\sum_{i=0}^{n-1}w_i \times 2^{i}
B2U(w)=i=0∑n−1wi×2i
u
→
=
u
′
→
\overrightarrow {u}=\overrightarrow{u'}
u=u′
补码符号扩展,在前面不断添加最高位数字即可
证明
B
2
T
t
+
k
(
[
w
t
−
1
w
t
−
1
w
t
−
2
⋯
w
0
]
)
=
−
2
t
+
k
−
1
∗
w
n
−
1
+
∑
i
=
0
t
+
k
−
2
2
i
∗
w
i
=
−
2
t
+
k
−
1
∗
w
t
−
1
+
2
t
+
k
−
2
∗
w
t
−
1
+
∑
i
=
0
t
+
k
−
3
2
i
∗
w
i
=
−
2
t
+
k
−
2
∗
w
t
−
1
+
∑
i
=
0
t
+
k
−
3
2
i
∗
w
i
⋯
=
−
2
t
−
1
∗
w
t
−
1
+
∑
i
=
0
t
−
2
2
i
∗
w
i
=
B
2
T
t
(
w
t
−
1
w
t
−
2
⋯
w
0
)
\begin{align} B2T_{t+k}([w_{t-1}w_{t-1}w_{t-2}\cdots w_0]) &= -2^{t+k-1}*w_{n-1}+\sum_{i=0}^{t+k-2}2^{i} *w_i \nonumber\\ &= -2^{t+k-1}*w_{t-1}+2^{t+k-2}*w_{t-1}+\sum_{i=0}^{t+k-3}2^{i} *w_i \nonumber\\ &=-2^{t+k-2}*w_{t-1}+\sum_{i=0}^{t+k-3}2^{i} *w_i \nonumber\\ &\cdots \nonumber \\ &=-2^{t-1} *w_{t-1} + \sum_{i=0}^{t-2}2^{i} *w_i \nonumber \\ &= B2T_{t}(w_{t-1}w_{t-2}\cdots w_0) \nonumber \end{align}
B2Tt+k([wt−1wt−1wt−2⋯w0])=−2t+k−1∗wn−1+i=0∑t+k−22i∗wi=−2t+k−1∗wt−1+2t+k−2∗wt−1+i=0∑t+k−32i∗wi=−2t+k−2∗wt−1+i=0∑t+k−32i∗wi⋯=−2t−1∗wt−1+i=0∑t−22i∗wi=B2Tt(wt−1wt−2⋯w0)
1.5 数位截断
无符号数的截断,直接取 k k k位即可。
证明
B
2
U
t
(
[
w
t
−
1
w
t
−
2
⋯
w
0
]
)
m
o
d
2
k
=
[
∑
i
=
0
t
−
1
w
i
∗
2
i
]
m
o
d
2
k
=
[
∑
i
=
0
k
−
1
w
i
∗
2
i
]
m
o
d
2
k
=
[
∑
i
=
0
k
−
1
w
i
∗
2
i
]
=
B
2
U
k
(
w
k
−
1
w
k
−
2
⋯
w
0
)
\begin{align} B2U_t([w_{t-1}w_{t-2}\cdots w_0]) \bmod 2^k &=[\sum_{i=0}^{t-1}w_i *2^i] \bmod 2^k \nonumber\\ &= [\sum_{i=0}^{k-1}w_i *2^i] \bmod 2^k \nonumber\\ &= [\sum_{i=0}^{k-1}w_i *2^i] \nonumber\\ &= B2U_k(w_{k-1}w_{k-2} \cdots w_0)\nonumber\\ \end{align}
B2Ut([wt−1wt−2⋯w0])mod2k=[i=0∑t−1wi∗2i]mod2k=[i=0∑k−1wi∗2i]mod2k=[i=0∑k−1wi∗2i]=B2Uk(wk−1wk−2⋯w0)
利用了
∀
i
>
=
k
,
2
i
m
o
d
2
k
=
0
\forall i>=k, 2^i \bmod2^k=0
∀i>=k,2imod2k=0
有符号数(补码)的截断
B
2
T
t
(
[
w
t
−
1
w
t
−
2
⋯
w
0
]
)
m
o
d
2
k
=
U
2
T
t
(
B
2
U
t
(
[
w
t
−
1
w
t
−
2
⋯
w
0
]
)
)
m
o
d
2
k
l
e
t
u
=
B
2
U
t
(
[
w
t
−
1
w
t
−
2
⋯
w
0
]
)
根据公式
(
3
)
=
[
u
−
(
i
×
2
t
)
]
m
o
d
2
k
=
u
m
o
d
2
k
=
U
2
T
t
(
B
2
U
t
(
[
w
t
−
1
w
t
−
2
⋯
w
0
]
)
m
o
d
2
k
)
\begin{align} B2T_t([w_{t-1}w_{t-2}\cdots w_0]) \bmod 2^k&= U2T_t(B2U_t([w_{t-1}w_{t-2}\cdots w_0])) \bmod 2^k \nonumber \\ &let\ u =B2U_t([w_{t-1}w_{t-2}\cdots w_0])\nonumber \\ 根据公式(3)\nonumber \\ &=[u-(i \times 2^{t})] \bmod 2^k\nonumber \\ &= u \bmod 2^k\nonumber\\ &= U2T_t(B2U_t([w_{t-1}w_{t-2}\cdots w_0])\bmod 2^k) \nonumber \\ \end{align}
B2Tt([wt−1wt−2⋯w0])mod2k根据公式(3)=U2Tt(B2Ut([wt−1wt−2⋯w0]))mod2klet u=B2Ut([wt−1wt−2⋯w0])=[u−(i×2t)]mod2k=umod2k=U2Tt(B2Ut([wt−1wt−2⋯w0])mod2k)
2. 整数的运算
2.1 整数加法
无符号整数加法
∀ x , y , 0 ≤ x , y < 2 w x + w u y = { x + y , x + y < 2 w x + y − 2 w , 2 w ≤ x + y < 2 w + 1 ( 溢出 ) \forall x,y, 0 \le x,y\lt2^w\\ x+^{u}_{w}y= \begin{cases} x+y, \quad x+y \lt 2^w\\ x+y-2^w,\quad 2^{w} \le x+y \lt 2^{w+1}(溢出) \end{cases} ∀x,y,0≤x,y<2wx+wuy={x+y,x+y<2wx+y−2w,2w≤x+y<2w+1(溢出)
检测无符号数
∀
x
,
y
,
0
≤
x
,
y
<
2
w
l
e
t
s
=
x
+
w
u
y
,
s
<
x
则发生溢出。
溢出时,
x
+
w
u
y
=
x
+
y
−
2
w
x
,
y
<
2
w
y
−
2
w
<
0
,
x
−
2
w
<
0
x
+
y
−
2
w
<
x
,
y
+
x
−
2
w
<
y
\forall x,y, 0 \le x,y\lt2^w\\ let\ s=x+^{u}_wy,s<x则发生溢出。\\ 溢出时,x+^{u}_wy=x+y-2^w\\ x,y \lt 2^w\\ y-2^{w} \lt 0,x-2^w \lt 0\\ x+y-2^w \lt x,y+x-2^w \lt y
∀x,y,0≤x,y<2wlet s=x+wuy,s<x则发生溢出。溢出时,x+wuy=x+y−2wx,y<2wy−2w<0,x−2w<0x+y−2w<x,y+x−2w<y
无符号数求反
−
w
u
x
=
{
0
,
x
=
0
2
w
−
x
,
x
≠
0
-^u_wx= \begin{cases} 0, \quad x=0\\ 2^w-x, x \ne 0 \end{cases}
−wux={0,x=02w−x,x=0
补码加法
∀
x
,
y
,
−
2
w
−
1
≤
x
,
y
≤
2
w
−
1
−
1
x
+
w
t
y
=
{
x
+
y
−
2
w
,
2
w
−
1
≤
x
+
y
x
+
y
,
−
2
w
−
1
≤
x
+
y
≤
2
w
−
1
x
+
y
+
2
w
,
x
+
y
≤
−
2
w
−
1
\forall x,y, -2^{w-1} \le x, y \le 2^{w-1} -1\\ x+^{t}_{w}y= \begin{cases} x+y-2^w, \quad 2^{w-1}\le x+y\\ x+y,\quad -2^{w-1} \le x+y \le 2^{w-1}\\ x+y+2^{w},\quad x+y\le -2^{w-1} \end{cases}
∀x,y,−2w−1≤x,y≤2w−1−1x+wty=⎩
⎨
⎧x+y−2w,2w−1≤x+yx+y,−2w−1≤x+y≤2w−1x+y+2w,x+y≤−2w−1
由于补码表示与无符号位表示相似
则我们可以转换为无符号再进行计算
x
+
w
t
y
=
U
2
T
w
(
T
2
U
w
(
x
)
+
T
2
U
w
(
y
)
)
=
U
2
T
w
[
(
x
w
−
1
2
w
+
x
+
y
w
−
1
2
w
+
y
)
m
o
d
2
w
]
=
U
2
T
w
[
(
x
+
y
)
m
o
d
2
w
]
\begin{align} x+^t_wy&= U2T_w(T2U_w(x)+T2U_w(y)) \nonumber \\ &= U2T_w[(x_{w-1}2^w+x+y_{w-1}2^w+y) \bmod 2^w]\nonumber \\ &= U2T_w[(x+y) \bmod 2^w]\nonumber \\ \end{align}
x+wty=U2Tw(T2Uw(x)+T2Uw(y))=U2Tw[(xw−12w+x+yw−12w+y)mod2w]=U2Tw[(x+y)mod2w]
检测补码加法中的溢出
s
=
x
+
w
t
y
x
>
0
,
y
>
0
,
s
≤
0
,
正溢出
x
<
0
,
y
<
0
,
s
≥
0
负溢出
s=x+^t_wy\\ x \gt 0, y \gt 0,s\le0,正溢出\\ x \lt 0,y\lt 0,s \ge 0负溢出
s=x+wtyx>0,y>0,s≤0,正溢出x<0,y<0,s≥0负溢出
补码的非
−
w
t
x
=
{
T
m
i
n
w
,
x
=
T
m
i
n
w
−
x
,
x
>
T
m
i
n
w
-^t_wx = \begin{cases} Tmin_w, \quad x=Tmin_w\\ -x,\quad x \gt Tmin_w \end{cases}
−wtx={Tminw,x=Tminw−x,x>Tminw
2.2 整数乘法
无符号乘法
x
∗
w
u
y
=
(
x
∗
y
)
m
o
d
2
w
x * ^u_wy=(x*y) \bmod 2^w
x∗wuy=(x∗y)mod2w
补码乘法
x ∗ w t y = U 2 T w ( ( x ∗ y ) m o d 2 w ) x * ^t_wy=U2T_w((x*y) \bmod 2^w) x∗wty=U2Tw((x∗y)mod2w)
证明
T
2
B
w
(
x
∗
w
t
y
)
=
U
2
B
w
(
x
′
∗
w
t
y
′
)
x
′
=
x
+
x
w
−
1
2
w
y
′
=
y
+
y
w
−
1
w
w
(
x
′
∗
y
′
)
m
o
d
2
w
=
(
x
+
x
w
−
1
2
w
)
(
y
+
y
w
−
1
2
w
)
m
o
d
2
w
=
(
x
y
)
m
o
d
2
w
T2B_w(x*^t_wy)=U2B_w(x'*^t_wy')\\ x' = x +x_{w-1}2^w\\ y' = y+y_{w-1}w^w\\ (x' * y') \bmod 2^w= (x +x_{w-1}2^w)(y+y_{w-1}2^w) \bmod 2^w=(xy) \bmod 2^w
T2Bw(x∗wty)=U2Bw(x′∗wty′)x′=x+xw−12wy′=y+yw−1ww(x′∗y′)mod2w=(x+xw−12w)(y+yw−12w)mod2w=(xy)mod2w
乘以2的
k
k
k次幂,左移
k
k
k位
B
2
U
w
+
k
(
[
x
w
−
1
x
w
−
2
⋯
0
]
)
=
∑
i
=
0
w
−
1
x
i
2
i
+
k
=
[
∑
i
=
0
w
−
1
x
i
2
i
]
×
2
k
=
x
2
k
B2U_{w+k}([x_{w-1}x_{w-2}\cdots 0]) = \sum_{i=0}^{w-1}x_i2^{i+k}=[\sum_{i=0}^{w-1}x_i2^i]\times2^k=x2^k
B2Uw+k([xw−1xw−2⋯0])=i=0∑w−1xi2i+k=[i=0∑w−1xi2i]×2k=x2k
3. 浮点数
3.1 浮点数表示
V
=
(
−
1
)
s
×
M
×
2
E
V=(-1)^s\times M \times2^E
V=(−1)s×M×2E
在内存中的布局
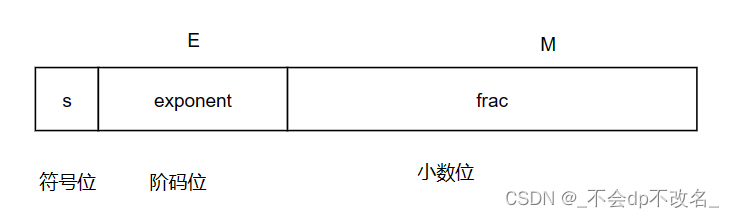
E
=
e
−
B
i
a
s
e
=
B
2
U
(
e
k
−
1
e
k
−
2
⋯
e
0
)
B
i
a
s
=
2
k
−
1
−
1
f
=
B
2
U
(
[
f
n
−
1
f
n
−
2
⋯
f
0
]
)
/
2
n
E=e-Bias\\ e=B2U(e_{k-1}e_{k-2}\cdots e_0)\\ Bias=2^{k-1}-1\\ f=B2U([f_{n-1}f_{n-2} \cdots f_0])/2^{n}
E=e−Biase=B2U(ek−1ek−2⋯e0)Bias=2k−1−1f=B2U([fn−1fn−2⋯f0])/2n
总体分三种情况
- 标准化值
阶码部分不全为0或不全为1
M = 1 + f M=1+f M=1+f - 非标准化值
阶码部分全为0
M = f M=f M=f - 特殊值
阶码全为1,小数域全为0,对应 − ∞ , + ∞ -\infin ,+\infin −∞,+∞,
小数域非0,对应 N a N NaN NaN,表示不是一个数。


![[WIP]Sora相关工作汇总VQGAN、MAGVIT、VideoPoet](https://img-blog.csdnimg.cn/direct/22aa1d0fcceb4c4081e72bd8d52d6907.png)