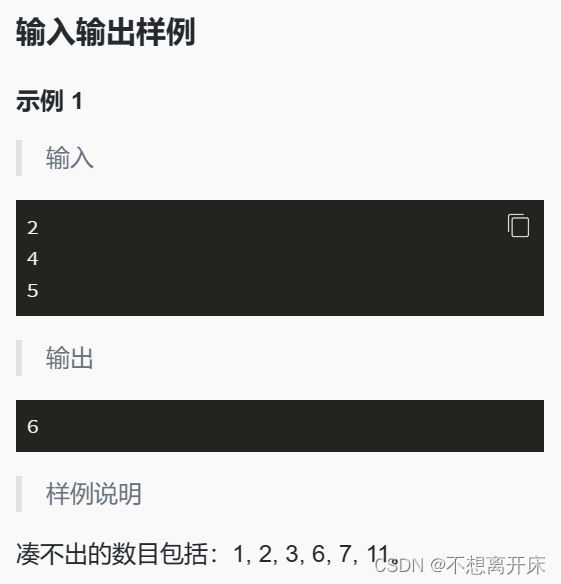
包子凑数

完全背包

完全背包问题和01背包的区别就是，完全背包问题每一个物品能取无限次。
思路：当n个数的最大公约数不为1，即不互质时，有无限多个凑不出来的，即n个数都可以表示成kn，k为常数且不为1。当n个数的最大公约数为1，到了某个数之后就全都可以凑出来。
根据本题的数据，可以直接遍历到10010就行

#include<iostream>
using namespace std;
//dp[i]表示i这个数可不可以被凑出来
int dp[10010];
//欧几里得算法求最大公约数
int gcd(int a,int b)
{
    return (b==0)?a:gcd(b,a%b);
}
int main()
{
    int n;
    cin>>n;
    int a[n],g;
    for(int i=0;i<n;i++) 
    {
        cin>>a[i];
        if(i==0) g=a[i];
        else g=gcd(g,a[i]);
    }
    if(g!=1)
    {
        cout<<"INF"<<endl;
        return 0;
    }
    dp[0]=1;
    //完全背包
    for(int i=0;i<n;i++)
    {
        for(int j=a[i];j<10010;j++)
        {
            dp[j]=max(dp[j],dp[j-a[i]]);
        }
    }
    int ans=0;
    for(int i=0;i<10010;i++)
    {
        if(!dp[i]) ans++;
    }
    cout<<ans<<endl;
    return 0;
}