一、概述
本篇blog写明了介绍的是STL(标准模板库)中的stack和queue,栈和队列虽然在处理数据的方式上有明显的不同,但它们作为操作受限的线性数据结构,在学习和应用中经常被放在一起讨论,以便更全面地理解数据结构的概念和使用。
在开始之前,先给大家做个知识补充,因为下面说的stack和queue实际上都是容器适配器。所以先介绍一下容器适配器。适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。虽然stack和queue中也可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配器,这是因为stack和队列只是对其他容器的接口进行了包装,STL中stack和queue默认使用deque。至于deque我们可以在最后面提一提。
二、stack
stack的介绍
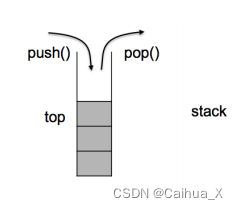
stack的接口
| 函数说明 | 接口说明 |
|
stack()
|
构造空的栈
|
|
empty()
|
检测
stack
是否为空
|
|
size()
|
返回
stack
中元素的个数
|
|
top()
|
返回栈顶元素的引用
|
|
push()
|
将元素
val
压入
stack
中
|
|
pop()
|
将
stack
中尾部的元素弹出
|
其实这些接口的使用都是十分清晰且基础的,没有二异性,不用专门写程序对其进行解释,不过我们可以通过题目来加固对这些接口的使用。
Leecode——最小栈


class MinStack {
public:
MinStack() {
}
void push(int val) {
_elem.push(val);
// 如果x小于_min中栈顶的元素,将x再压入_min中
if (_min.empty() || val <= _min.top())
_min.push(val);
}
void pop() {
// 如果_min栈顶的元素等于出栈的元素,_min顶的元素要移除
if (_min.top() == _elem.top())
_min.pop(); // 保证 _min 的数据是有效的
_elem.pop();
}
int top() {
return _elem.top();
}
int getMin() {
return _min.top();
}
private:
// 创建这两个对象,马上就使用里面的接口来实现这个题目
stack<int> _elem;
stack<int> _min;
};
牛客——栈的压入、弹出序列


class Solution {
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
if (pushV.size() != popV.size())
return false;
// 用s来模拟入栈与出栈的过程
int outIdx = 0;
int inIdx = 0;
stack<int> s;
while (outIdx < popV.size())
{
// 如果s是空,或者栈顶元素与出栈的元素不相等,就入栈
while (s.empty() || s.top() != popV[outIdx])
{
if (inIdx < pushV.size())
s.push(pushV[inIdx++]);
else
return false;
}
// 栈顶元素与出栈的元素相等,出栈
s.pop();
outIdx++;
}
return true;
}
};逆波兰表达式求值
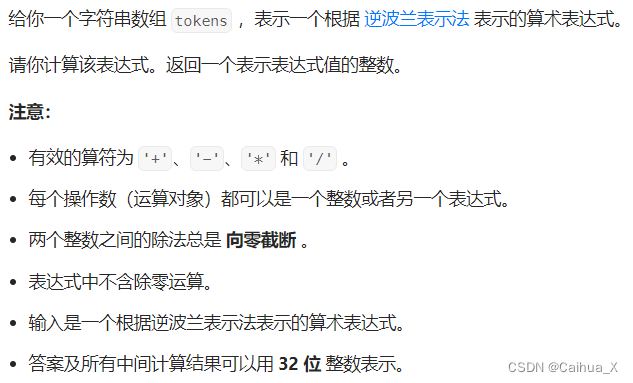

class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> s; // 使用栈s来存储中间计算结果
for (size_t i = 0; i < tokens.size(); ++i) // 遍历tokens中的每个元素
{
string& str = tokens[i];
// 判断str是否是操作符
if (!("+" == str || "-" == str || "*" == str || "/" == str)) {
// 如果str是数字,将其转换为int并入栈
s.push(atoi(str.c_str()));
}
else {
// 如果str是操作符,从栈中弹出两个元素作为操作数
int right = s.top(); // 第二个操作数
s.pop();
int left = s.top(); // 第一个操作数
s.pop();
// 根据操作符计算结果,并将结果入栈
switch (str[0]) {
case '+':
s.push(left + right); // 加法运算
break;
case '-':
s.push(left - right); // 减法运算
break;
case '*':
s.push(left * right); // 乘法运算
break;
case '/':
s.push(left / right); // 除法运算,已假设除数不为0
break;
}
}
}
// 返回栈顶元素,即整个表达式的计算结果
return s.top();
}
};
这样我们就使用了接口实现了一些比较复杂的算法。怎么样,是不是很有成就感。
三、queue
queue的介绍
stack的接口
|
函数声明
|
接口说明
|
|
queue()
|
构造空的队列
|
|
empty()
|
检测队列是否为空,是返回
true
,否则返回
false
|
|
size()
|
返回队列中有效元素的个数
|
|
front()
|
返回队头元素的引用
|
|
back()
|
返回队尾元素的引用
|
|
push()
|
在队尾将元素
val
入队列
|
|
pop()
|
将队头元素出队列
|
这些接口和stack的十分类似。相信大家稍微变通一下就可以知道了。在这里我就不进行举例了。
四、priority_queue的介绍和使用
priority_queue的接口
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使priority_queue。注意:默认情况下priority_queue是大堆(大顶堆)。
| 函数接口 | 接口说明 |
|
priority_queue()/priority_queue(first,
last)
|
构造一个空的优先级队列
|
|
empty( )
|
检测优先级队列是否为空,是返回
true
,否则返回
false
|
|
top( )
|
返回优先级队列中最大
(
最小元素
)
,即堆顶元素
|
|
push(x)
|
在优先级队列中插入元素
x
|
|
pop
()
|
删除优先级队列中最大
(
最小
)
元素,即堆顶元素
|
接口不用一个一个试了,写两个程序带大家理解一下这个priority_queue。
程序例子
默认情况下,priority_queue是大堆
#include <iostream>
#include <vector>
#include <queue>
#include <functional> // greater算法的头文件
using namespace std;
void TestPriorityQueue()
{
// 默认情况下,创建的是大堆,其底层按照小于号比较
vector<int> v{ 3,2,7,6,0,4,1,9,8,5 };
priority_queue<int> q1;
for (auto& e : v)
q1.push(e);
cout << q1.top() << endl;
// 输出 9
// 如果要创建小堆,将第三个模板参数换成greater比较方式
priority_queue<int, vector<int>, greater<int>> q2(v.begin(), v.end());
cout << q2.top() << endl;
// 输出 0
}
int main()
{
TestPriorityQueue();
return 0;
}#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
#include <queue>
#include <functional> // greater算法的头文件
using namespace std;
class Date
{
public:
Date(int year = 1900, int month = 1, int day = 1)
: _year(year)
, _month(month)
, _day(day)
{}
// 重载 < 符号
bool operator<(const Date& d)const
{
return (_year < d._year) ||
(_year == d._year && _month < d._month) ||
(_year == d._year && _month == d._month && _day < d._day);
}
// 重载 > 符号
bool operator>(const Date& d)const
{
return (_year > d._year) ||
(_year == d._year && _month > d._month) ||
(_year == d._year && _month == d._month && _day > d._day);
}
// friend 使其的封装性失效了 ,这行代码的意思是:
// “我信任ostream& operator<<函数,允许它访问我的所有内容,包括私有成员。
friend ostream& operator<<(ostream& _cout, const Date& d)
{
_cout << d._year << "-" << d._month << "-" << d._day;
return _cout;
}
private:
int _year;
int _month;
int _day;
};
void TestPriorityQueue()
{
// 大堆,需要用户在自定义类型中提供<的重载
priority_queue<Date> q1;
q1.push(Date(2018, 10, 29));
q1.push(Date(2018, 10, 28));
q1.push(Date(2018, 10, 30));
cout << q1.top() << endl;
// 2018-10-30
// 如果要创建小堆,需要用户提供>的重载
priority_queue<Date, vector<Date>, greater<Date>> q2;
q2.push(Date(2018, 10, 29));
q2.push(Date(2018, 10, 28));
q2.push(Date(2018, 10, 30));
cout << q2.top() << endl;
//2018-10-28
}
int main()
{
TestPriorityQueue();
return 0;
}讲到这里实际上,我们已经把该节任务,stack和queue讲完了,毕竟他们都只是容器适配器,最终实现还是放在C++的容器里面的。比如list和vector,但是其实这两个一般默认的是用deque来实现的。所以想和大家再介绍一下deque。
五、底层的deque(仅了解)
deque的介绍
deque的缺陷
与vector比较,deque的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不 需要搬移大量的元素,因此其效率是必vector高的。与list比较,其底层是连续空间,空间利用率比较高,不需要存储额外字段。但是,deque有一个致命缺陷:不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作为stack和queue的底层数据结构
deque作为stack和queue的底层默认容器的原因
六、总结
这篇文章深入探讨了C++标准模板库(STL)中的栈(stack)和队列(queue),以及容器适配器的概念。通过解释栈和队列的工作原理、接口、以及使用场景,文章展示了这两种数据结构在处理特定数据序列时的效率和便利性。同时,通过引入deque(双端队列)作为stack和queue的默认底层容器,文章阐述了其在特定场景下相比其他容器(如vector和list)的优势,同时指出了deque的主要缺陷和在特定应用场景中的优化选择。希望大家能有所收获!