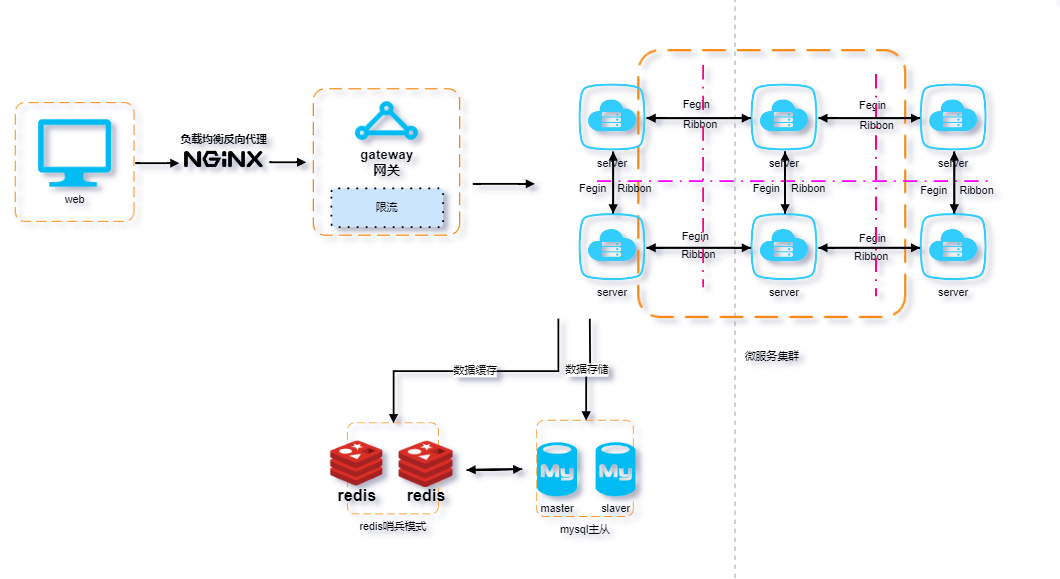
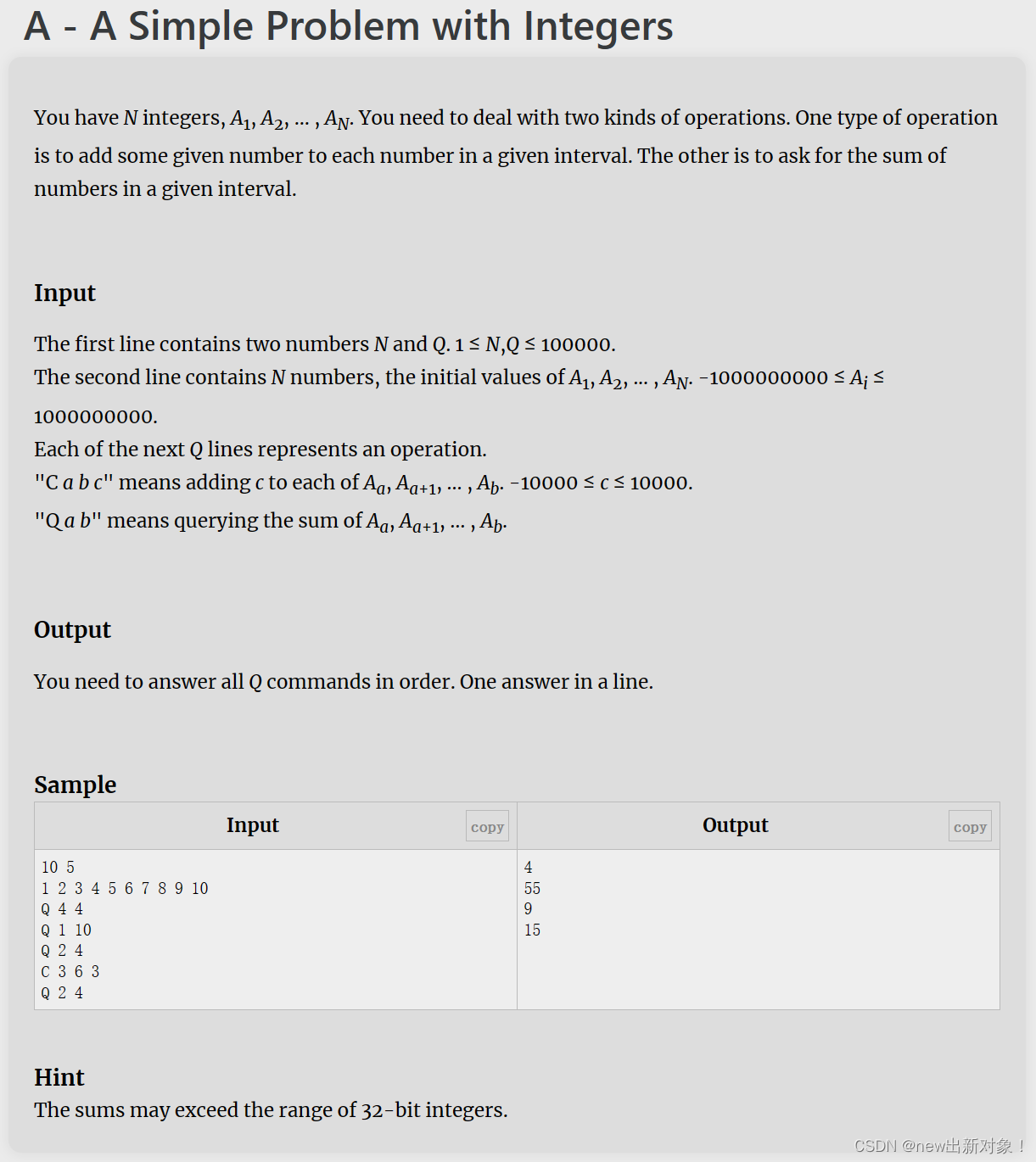
目录
一、向量和矩阵的微分
1. 向量对标量的导数
2. 矩阵对标量的导数
2.1 矩阵对标量的导数的运算公式
2.2 标量函数对向量的导数:
2.3 向量函数对向量的导数
二、函数极值的问题
三、有约束条件的函数极值问题
四、n元函数的Taylor
一、向量和矩阵的微分
1. 向量对标量的导数
n维向量函数:f(t) = [f1(t), f2(t), ..., fn(t)]T,对标量自变量t的导数定义为:
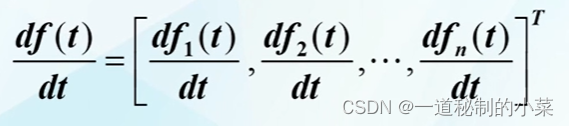
2. 矩阵对标量的导数

2.1 矩阵对标量的导数的运算公式
矩阵对标量的导数的运算公式:

2.2 标量函数对向量的导数:

称为梯度或者偏导数。
2.3 向量函数对向量的导数


二、函数极值的问题


接下来我们对n元进行推广:

三、有约束条件的函数极值问题

推广到n元方程中:

四、n元函数的Taylor