LeetCode-124. 二叉树中的最大路径和【树深度优先搜索动态规划二叉树】

news2025/10/31 8:20:32

LeetCode-124. 二叉树中的最大路径和【树深度优先搜索动态规划二叉树】

题目描述：
解题思路一：递归。return max(max(l_val, r_val) + node.val, 0)
解题思路二：0
解题思路三：0

题目描述：

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

示例 1：
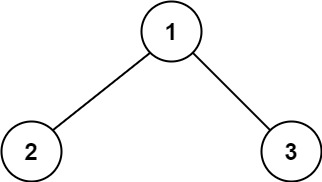
在这里插入图片描述
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 10⁴]
-1000 <= Node.val <= 1000

解题思路一：递归。return max(max(l_val, r_val) + node.val, 0)

空节点的最大贡献值等于 0。
非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和（对于叶节点而言，最大贡献值等于节点值）。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        ans = -inf
        def dfs(node: Optional[TreeNode]) -> int:
            if node is None:
                return 0  # 没有节点，和为 0
            l_val = dfs(node.left) # 左子树最大链和
            r_val = dfs(node.right) # 右子树最大链和
            nonlocal ans
            ans = max(ans, l_val + r_val + node.val) # 两条链拼成路径
            return max(max(l_val, r_val) + node.val, 0) # 当前子树最大链和
        dfs(root)
        return ans