题目如下：

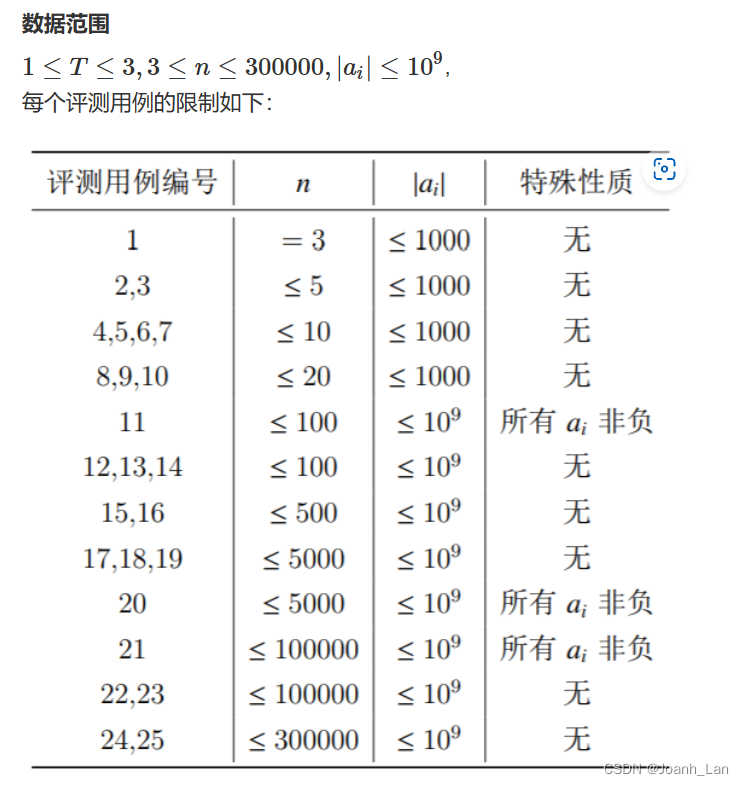
思路 or 题解

如果我们可以发现前缀和，对于这个题有特殊的性质，这个题就不能做出来了，不然你会想我一样卡好长时间，从不知所措。

• $a_{i+1}+=a_i,a_{i-1}+=a_i,a_i-=2a_i$ , $i\ge 2andi\le n-1$

考虑前缀和:对于每次操作,相当于交换了$s[i-1]$ 和 $s[i]$ ,对于$s[i+1]$ 无影响,要求|a|最小即将前缀和数组按升序排列,找出前缀和中的最大差值即可即可(反证法可证)
令 $s[0]=0$ ,由于交换对 $s[i+1]$ 无影响,这样数据的两端就确定下来了且是无法改变的.

由于头尾两点无法改变,我们只有两条路径可以使序列的差值最小:

• $s[0]$ -> 最小值 -> 最大值 -> $s[n]$
• $s[0]$ -> 最大值 -> 最小值 -> 最大值.

以下标 $i$ 为 $x$ 轴,以 $s[i]$ 为 $y$ 轴,比较两条曲线可知第一种策略下最多只有两层的波折 —— 需要隔1个跳, 而在第二种策略下最多有三层的波折——需要隔两跳,隔着跳的越多,也就意味着间隔越大,所以第一种策略更优!

思考贪心的策略:假设初值较小,终值较大(因为显然我们在乎的并不是实际的序列,而仅仅是序列的最大差值 —— 而这不论是 s0<=sn,还是sn <= s0, 还是sn<=s0 情况下都是唯一的). s0 到最小值段隔着跳,最大值到 sn 段隔着跳,最小值段到最大值段直接收录剩下的元素.(注意:奇数和偶数情况略有不同)

AC 代码如下：

#define ll long long
const int N = 300009;
int n, s[N], a[N];
bool st[N];
void solve()
{
    cin >> n;
    // memset(st, 0, 1 + n);
    fill(st, st + 1 + n, 0);
    s[0] = 0;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        s[i] = s[i - 1] + a[i];
    }
    int s0 = s[0], sn = s[n];
    if (s0 > sn)
        swap(s0, sn);
    sort(s, s + 1 + n);
    for (int i = 0; i <= n; i++)
    {
        if (s[i] == s0)
        {
            s0 = i;
            break;
        }
    }
    for (int i = n; i >= 0; i--)
    {
        if (s[i] == sn)
        {
            sn = i;
            break;
        }
    }
    int l = 0, r = n;
    for (int i = s0; i >= 0; i -= 2)
        a[l++] = s[i], st[i] = true;
    for (int i = sn; i <= n; i += 2)
        a[r--] = s[i], st[i] = true;
    for (int i = 0; i <= n; i++)
        if (!st[i])
            a[l++] = s[i];
    int ans = 0;
    for (int i = 1; i <= n; i++)
        ans = max(ans, abs(a[i] - a[i - 1]));
    cout << ans << '\n';
}
signed main()
{
    buff;
    int _;
    cin >> _;
    while (_--)
        solve();
}