---

前言

学习python数据结构与算法，学习常用的算法，
b站学习链接

53.栈和队列的应用：迷宫问题

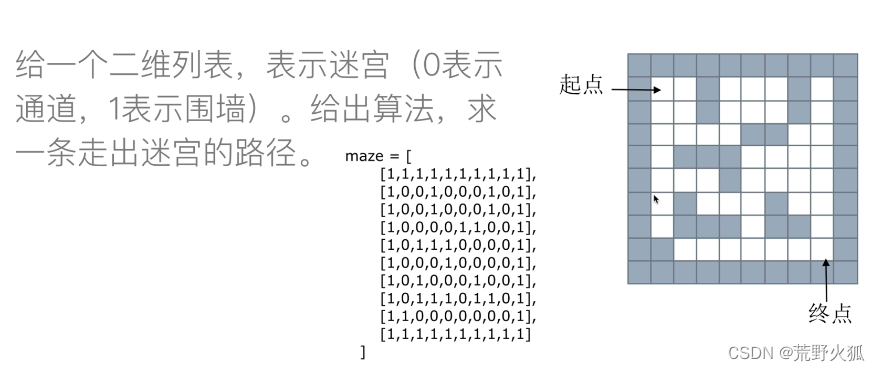
先讲如何用栈实现走迷宫的思路： 栈----深度优先搜索
回溯法
思路：从一个节点开始，任意找下一个能走的点，当找到不能走的点时，退回上一个点寻找是否有其他方向的点。
使用栈来存储当前路径
比方说：规定只能走上下左右，优先顺序是上，右，下，左，有路可以走就走，标记走过的路，走过的路不能走，，把路径进栈，当有路不能走时，出栈。

这时，走不通了，回溯到上一步，看能不能走，因为标记过的路也不能走，所以一直出栈到第4步走的路，

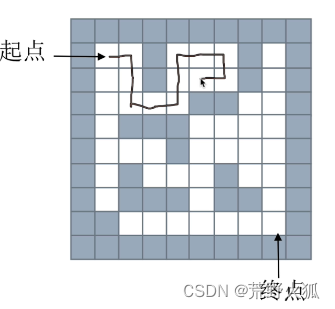
按照这个思路一直走到终点。

54.使用栈解决迷宫问题

1是墙，0是路

maze = [
    [1,1,1,1,1,1,1,1,1,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,0,0,1,1,0,0,1],
    [1,0,1,1,1,0,0,0,0,1],
    [1,0,0,0,1,0,0,0,0,1],
    [1,0,1,0,0,0,1,0,0,1],
    [1,0,1,1,1,0,1,1,0,1],
    [1,1,0,0,0,0,0,0,0,1],
    [1,1,1,1,1,1,1,1,1,1]
]

lambda的用法
主要用法是：
将lambda函数赋值给一个变量，通过这个变量间接调用该lambda函数。
例如，执行语句add=lambda x, y: x+y，定义了加法函数lambda x, y: x+y，并将其赋值给变量add，这样变量add便成为具有加法功能的函数。例如，执行add(1,2)，输出为3。
所以这里dir()

优先顺序上下左右可以自己定，不影响最终能否找到路。

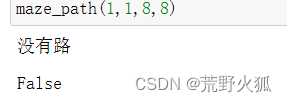
故意把路堵住

55.使用队列进行迷宫问题：介绍

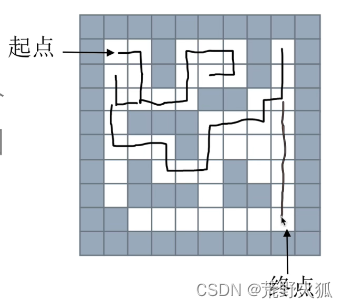
队列 —广度优先搜索 会一个一个分支去找路径最短的
思路：
从一个节点开始，寻找所有接下来能继续走的点，继续不断寻找，直到找到出口
使用队列存储当前正在考虑的点。

一开始有两条路可以走，将这两条路径都存在队列里，假设往右走是第一个，往下走是第二个

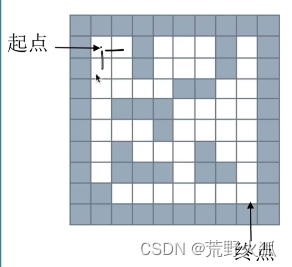
然后第一个出队，往下走的路径第三个进队，第二个出队，往下走的路径第四个进队。

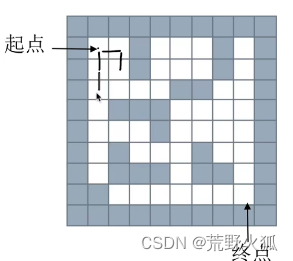
走过的路标记，不通的路就出队，队列只存当前可以走的路径。

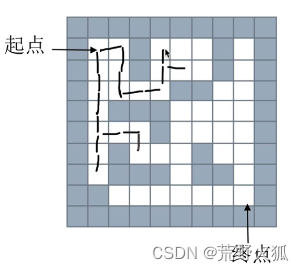
最终走到终点，这个路径且是最短的。

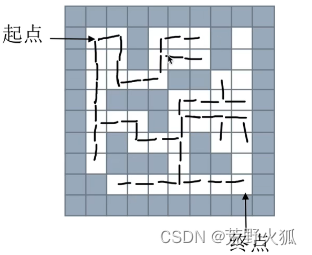
简化到下图，右边矩形里的队列里存的当前要走的路径。

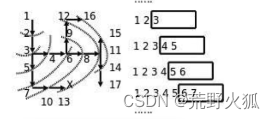
如何找到终点把路径输出出来呢？假设7是终点
开两个列表
第一个列表存当前走的路，第二个列表存上一个路的下标，然后把它一一对应，倒着输出就是完整的路径。
1是起点，上一个路没有，存-1，

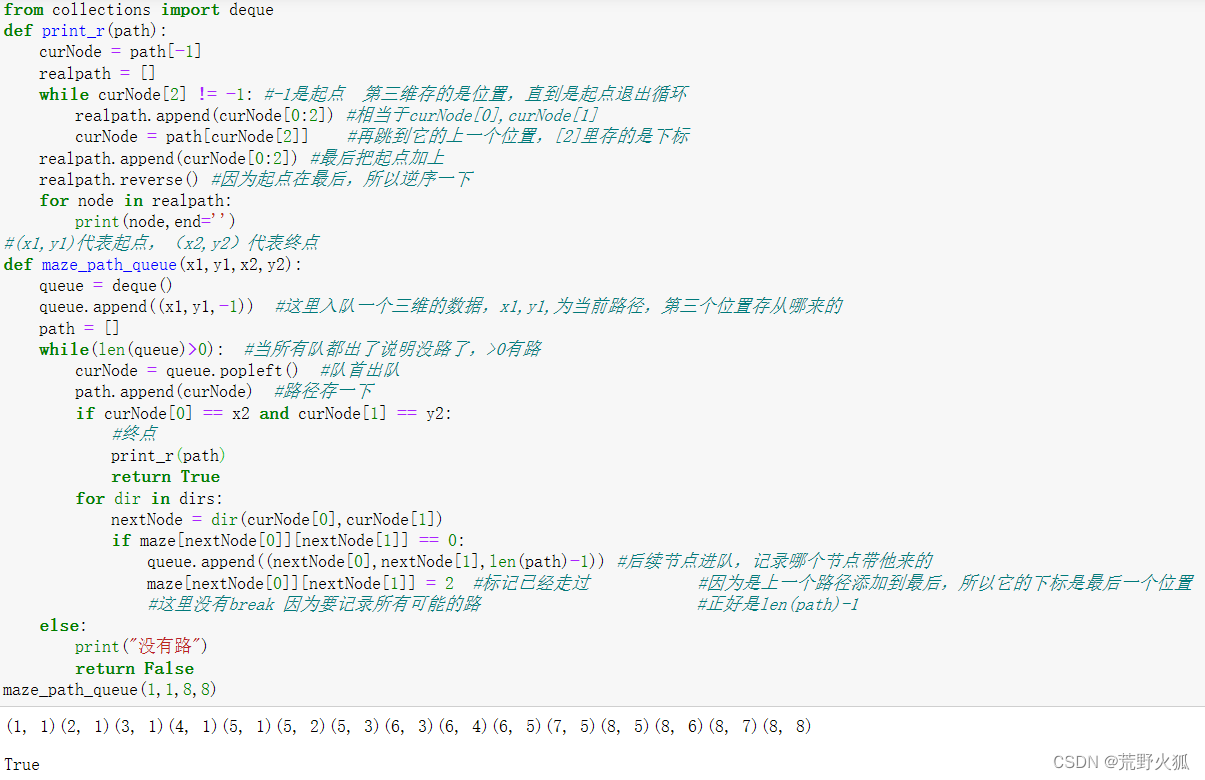
56.使用队列进行迷宫问题：实现：

这个程序有点绕：
主要在存上一个路的下标和输出路径，
存路径用这个打比方，1是起点，7是终点，首先进1，然后出1 进2，把1 存在新的列表path里，1有三维数据（当前路径和-1），出2进3，再把2存在列表里，2有三维数据（当前路径和上一个路径在列表的下标，也就是0，或者说是len(list)-1）,然后出3先进4再进5（人为规定优先级上右下左），然后3存到列表三个数据（当前路径和1）然后先出4进6（一个方向一个方向出）把4存到列表（当前路径和2）再出5进7，把5存到列表（当前路径和2，因为4要在下一个循环存，所里当前还是2），出6先9再进8，存6的路径和3(因为5还没有存，所以是3），出7，存当前路径和4(此时6没有存5存了)，发现到达终点
最终退出循环。

输出路径：
新创一个列表，将当前路径为最后一个路径，判断不是起点就找上一个路径在path里的位置，然后找到路径继续append到新列表里，直到起点退出，再把起点加上，倒序输出新列表。

前面迷宫和方向和前面栈的一样

总结

用栈和队列解决迷宫问题，队列能找到最短路径，栈能找到路径不保证最短。

---