目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2021年,FA Hashim等人受到自然界中蜜獾狩猎行为启发,提出了蜜獾算法((Honey Badger Algorithm,HBA)。
2.算法原理
2.1算法思想
蜜獾以其独特的狩猎方式而闻名,它利用嗅觉定位猎物,通过挖掘来捕获目标。虽然蜜獾喜欢蜂蜜,但并不擅长找到蜂巢。与此不同的是,蜂蜜向导鸟擅长定位蜂巢,却无法获得蜂蜜。因此,蜜獾会依靠蜂蜜向导鸟的帮助找到蜂巢,并与其共享收获。HBA主要分为挖掘阶段和采蜜阶段。

2.2算法过程
定义强度:
蜜獾的嗅觉强度不仅与猎物的集中强度有关,还与猎物和蜜獾之间的距离有关。Ii是猎物的气味强度,气味强度越高,蜜獾运动越快:
I
i
=
r
2
×
S
4
π
d
i
2
S
=
(
x
i
−
x
i
+
1
)
2
d
i
=
x
p
rey
−
x
i
(1)
\begin{aligned}I_i&=r_2\times\frac{S}{4\pi d_i^2}\\S&=(x_i-x_{i+1})^2\\d_i&=x_{p\text{rey}} - x_i\end{aligned}\tag{1}
IiSdi=r2×4πdi2S=(xi−xi+1)2=xprey−xi(1)
更新密度因子:
密度因子w控制时变随机化,以确保勘探到开发的平稳过渡。当更新随着迭代次数减少时,密度因子w也会减少随机化:
w
=
C
exp
(
−
t
t
m
a
x
)
(2)
w=\text{C}\exp(\frac{-t}{t_{\mathrm{max}}})\tag{2}
w=Cexp(tmax−t)(2)
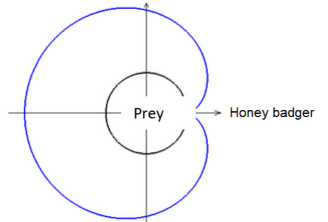
挖掘阶段:
在挖掘阶段,蜜獾运动范围类似于心形:
X
n
e
n
,
=
x
p
r
e
y
+
F
×
β
×
I
×
x
p
r
e
y
+
F
×
r
3
×
w
×
d
i
×
∣
cos
(
2
π
r
4
)
×
[
l
−
cos
(
2
π
r
5
)
]
∣
(3)
\begin{aligned} X_{nen}, =x_{prey}+F\times\beta\times I\times x_{prey}+F\times r_{3}\times w\times d_{i}\times |\cos(2\pi r_{4})\times[\text{l}-\cos(2\pi r_{5})]| \end{aligned}\tag{3}
Xnen,=xprey+F×β×I×xprey+F×r3×w×di×∣cos(2πr4)×[l−cos(2πr5)]∣(3)
其中
x
p
r
e
y
x_{prey}
xprey是猎物的全局最优位置,
β
\beta
β是蜜獾获取食物的能力。F是改变搜索方向参数:
F
=
{
1
i
f
−
1
e
l
s
e
,
r
6
≤
0.5
(4)
F=\begin{cases}1&if\\-1&else,\end{cases}r_6\leq0.5\tag{4}
F={1−1ifelse,r6≤0.5(4)
采蜜阶段:
蜜獾跟随导蜜鸟找到蜂巢:
x
n
e
w
=
x
p
v
e
y
+
F
×
r
7
×
w
×
d
i
(5)
x_{new}=x_{pvey}+F\times r_{7}\times w\times d_{i}\tag{5}
xnew=xpvey+F×r7×w×di(5)
伪代码:

3.结果展示
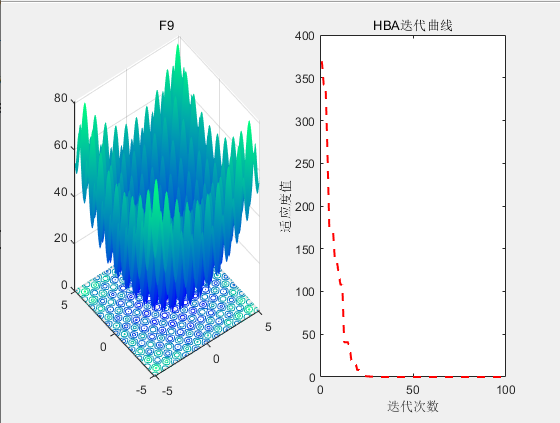
4.参考文献
[1] Hashim F A, Houssein E H, Hussain K, et al. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems[J]. Mathematics and Computers in Simulation, 2022, 192: 84-110.