【Leetcode每日一题】动态规划 - 不同路径（难度⭐⭐）（49）

news2025/10/31 16:05:43

1. 题目解析

题目链接：63. 不同路径 II

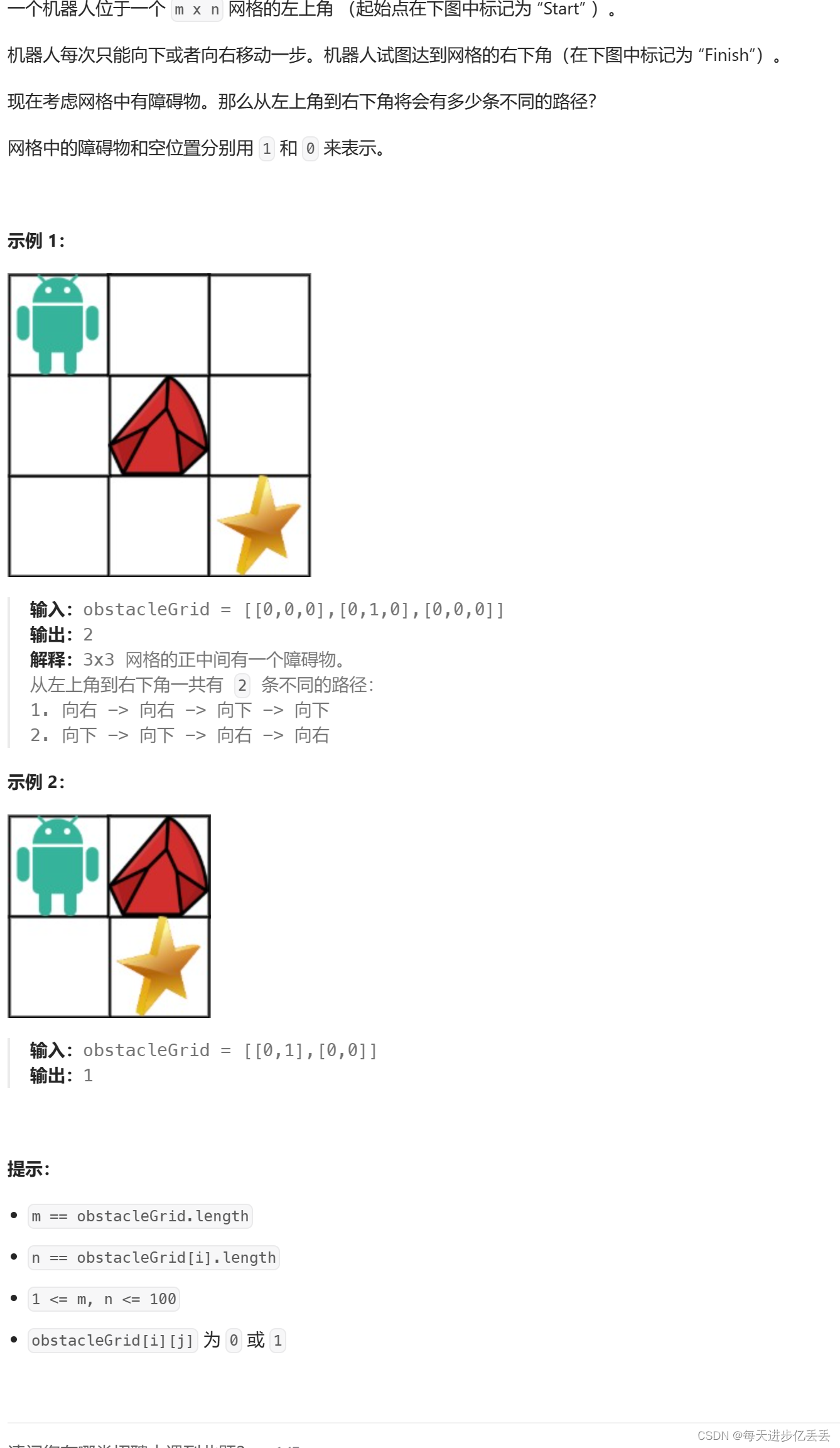
这个问题的理解其实相当简单，只需看一下示例，基本就能明白其含义了。

2.算法原理

这个问题就像是在一个迷宫中找路，只不过这个迷宫有些格子是不能走的，也就是那些“障碍物”。我们的任务是找出从起点到终点的所有可能路径。

想象一下，你站在一个格子上，你想知道到达这个格子有多少种走法。那你只需要看看你是从哪个格子走过来的。是不是只有两种可能：要么是从上面的格子走下来，要么是从左边的格子走过来？

但这里有个问题，如果上面的格子或左边的格子是障碍物，那你就不能从那里走过来。所以，我们得检查每个格子，看它上面和左边的格子是不是障碍物。

接下来，我们就来详细说说怎么计算这些走法：

状态表示：
用dp[i][j]来表示到达第i行第j列的格子有多少种走法。
状态转移：
到达dp[i][j]这个格子，要么是从dp[i-1][j]这个格子走下来，要么是从dp[i][j-1]这个格子走过来。所以，走法的数量就是这两个格子走法数量的和。当然，如果这两个格子有障碍物，那它们的走法数量就是0。
初始化：
为了计算方便，我们通常在迷宫的外面多加一行和一列。这样，起点就变成了dp[1][1]，并且dp[1][0]这个格子的走法数量就是1，因为我们只能从起点开始走。
填表顺序：
我们按照从上到下、从左到右的顺序来填这个表格。这样，当我们计算dp[i][j]的时候，dp[i-1][j]和dp[i][j-1]都已经被计算过了。
返回值：
最后，我们要找的是从起点到终点的走法数量，也就是dp[m][n]，其中m和n分别是迷宫的行数和列数。

3.代码编写

class Solution 
{
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
    {
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        dp[0][1] = 1;
        for(int i = 1; i <= m; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                if(obstacleGrid[i - 1][j - 1] == 0)//减一是为了dp映射会ob，dp行列都加一了
                {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m][n];
    }
};