本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：算法从入门到精通
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

岛屿的最大面积

题目来源：Leetcode695岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

算法原理：

本题是在之前岛屿数量的基础上，还是采用BFS来进行解决。
定义一个count计数器，在每找到一个联通块就对计数器++。

class Solution 
{
     //向量数组
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    bool vis[51][51];
    int m,n;
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) 
    {
        m=grid.size(),n=grid[0].size();

        int ret=0;
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(grid[i][j]==1&&vis[i][j]==false)
                {
                	//取的是最大联通块的面积
                    ret=max(ret,bfs(grid,i,j));
                }
            }
        }
        return ret;
    }
    int bfs(vector<vector<int>>& grid,int i,int j)
    {
    	//定义一个计数器
        int count=0;
        queue<pair<int, int>> q;
        q.push({i,j});
        vis[i][j]= true;
        count++;
        while(q.size())
        {
            auto [a,b]=q.front();
            q.pop();
            for(int k=0;k<4;k++)
            {
                int x=a+dx[k],y=b+dy[k];
                //防止越界
                if(x>=0 && x<m && y>=0 && y<n && y<n && grid[x][y]==1 && vis[x][y]==false)
                {
                    //满足情况入队
                    q.push({x,y});
                    vis[x][y]=true;
                    //计数器++
                    count++;
                }
            }
        }
        return count;
    }
};

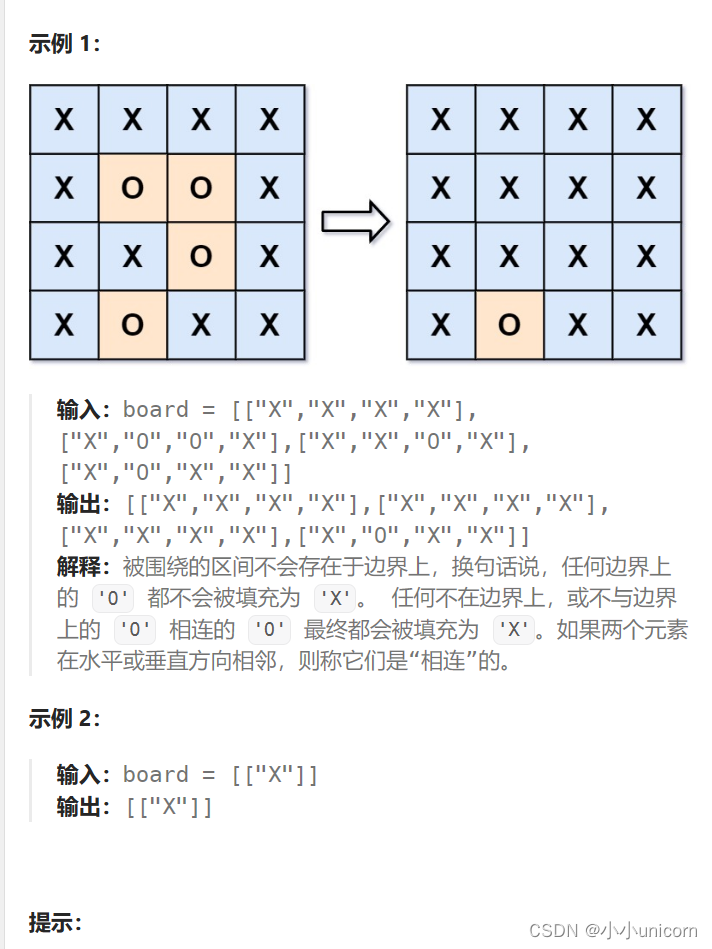
被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

算法原理：

本题我们要用正难则反的思想来解决此问题。
因为之前我们的floodfill算法在BFS过程中是边搜索边修改，如果要是碰到边界情况，那么说明此时遍历的是不符合要求的，我们需要还原回去，但是在我们用flloodfill算法中已经将他们修改成了’X’,问题就会变得复杂。

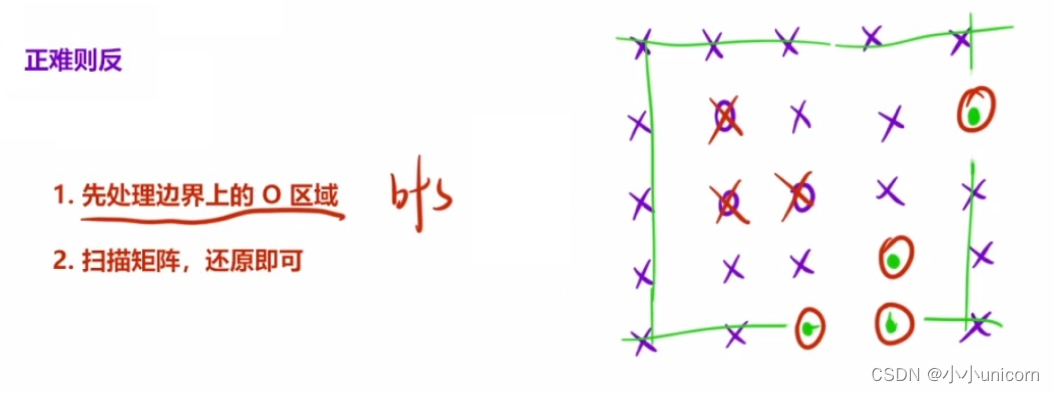
那么我们就要反过来想：
我们先处理边界情况，在边界情况用bfs将那一整个联通快找出来，这个联通快我们是不能要的也就是不符合要求的，我们可以先将这个不符合要求的这一联通快修改成无关字符，例如$.$或者$Y$之类，边界情况处理完那么边界范围内搜索出来的结果肯定就是符合要求的，我们根据题目要求将他们修改。
最后边界里面处理完了之后，我们要把刚才边界处理的联通快再还原回去。问题就解决了。

代码实现：

class Solution 
{
    //向量数组
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    int m;
    int n;
public:
    void solve(vector<vector<char>>& board) 
    {
        m=board.size(),n=board[0].size();

        //1.先处理边界情况上的'0'联通块，全部修改成'.'
        //处理行
        for(int j=0;j<n;j++)
        {
            //第一行
            if(board[0][j]=='O')
                bfs(board,0,j);
            //最后一行
            if(board[m-1][j]=='O')
                bfs(board,m-1,j);
        }
        //处理列
        for(int i=0;i<m;i++)
        {
            //第一列：
            if(board[i][0]=='O')
                bfs(board,i,0);
            //最后一列
            if(board[i][n-1]=='O')
                bfs(board,i,n-1);
        }
        //2.还原
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(board[i][j]=='O')
                    board[i][j]='X';
                else if(board[i][j]=='.')
                    board[i][j]='O';
            }
        }
    }
    void bfs(vector<vector<char>>& board,int i,int j)
    {
        queue<pair<int, int>> q;
        q.push({i,j});
        board[i][j]= '.';
        while(q.size())
        {
            auto [a,b]=q.front();
            q.pop();
            for(int k=0;k<4;k++)
            {
                int x=a+dx[k],y=b+dy[k];
                //防止越界
                if(x>=0 && x<m && y>=0 && y<n && y<n&& board[x][y]=='O')
                {
                    //满足情况入队
                    q.push({x,y});
                    board[x][y]='.';
                }
            }
        }
    }
};