目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2022年,Naruei等人受到自然界动物猎食过程启发,提出了猎人猎物算法(Hunter-Prey Optimization, HPO)。
2.算法原理
2.1算法思想
HPO模拟了自然界中动物的捕猎过程,算法的核心思想是:猎人追逐被捕猎物远离群体的个体,并根据被捕猎物的平均位置调整自身位置;而被捕猎物也动态调整自身位置以更安全地躲避捕食者。
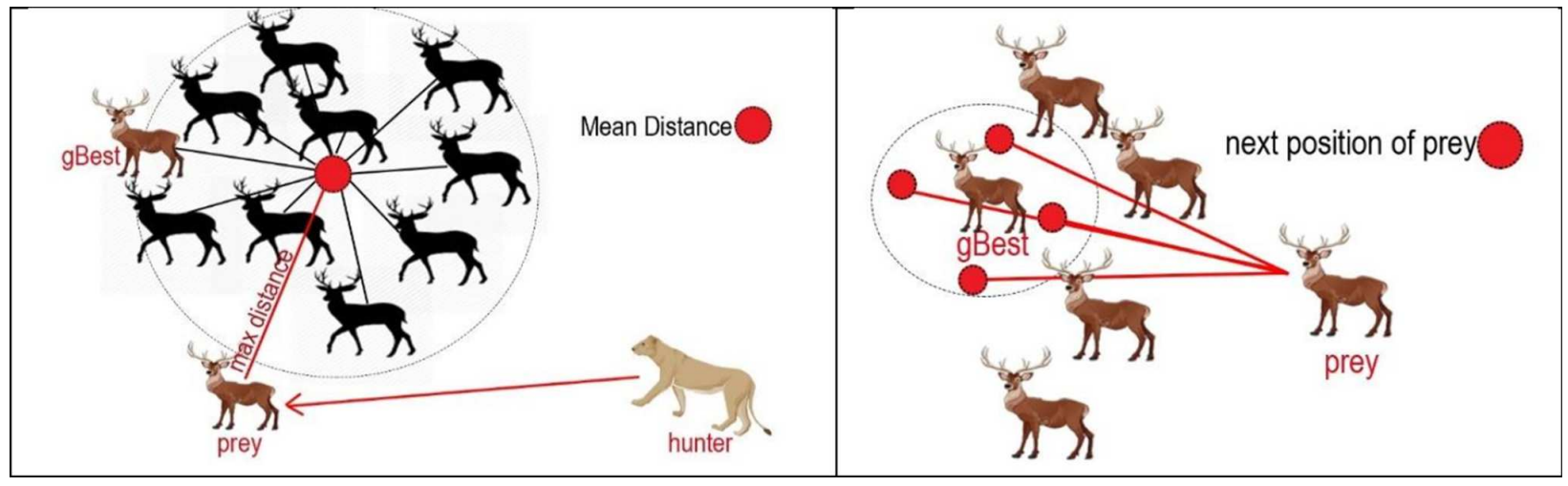
2.2算法过程
猎人捕猎:
x
(
t
+
1
)
=
x
(
t
)
+
0.5
[
(
2
C
Z
P
pos
−
x
(
t
)
)
+
(
2
(
1
−
C
)
Z
μ
−
x
(
t
)
)
]
(1)
\begin{aligned}\boldsymbol{x}(t+1)&=\boldsymbol{x}(t)+0.5[(2C\boldsymbol{Z}\boldsymbol{P}_{\text{pos}}-\boldsymbol{x}(t))+(2(1-C)\boldsymbol{Z}\boldsymbol{\mu}-\boldsymbol{x}(t))]\end{aligned}\tag{1}
x(t+1)=x(t)+0.5[(2CZPpos−x(t))+(2(1−C)Zμ−x(t))](1)
其中,x(t)表示猎人当前时刻的位置;x(t+1)表示猎人下一时刻的位置;Ppos是当前猎人所追逐猎物的位置,一般选择距离种群平均位置最远个体作为Ppos;μ是当前种群中所有个体位置的平均值;C是探索与开发之间的平衡参数;Z 是算法的自适应参数;μ、C 和 Z 的计算公
式分别为:
μ
=
1
N
∑
i
=
1
N
x
i
C
=
1
−
t
×
(
0.98
/
M
a
x
I
t
)
Z
=
R
2
×
I
D
X
+
R
3
⊗
(
∼
I
D
X
)
I
D
X
=
R
1
>
C
(2)
\begin{aligned} &\boldsymbol{\mu}=\frac1N\sum_{i=1}^{N}\boldsymbol{x}_{i} \\ &C=1-t\times(0.98/MaxIt) \\ &Z=R2\times\mathbf{IDX}+R3\otimes(\sim\mathbf{IDX}) \\ &\mathbf{IDX}=\mathbf{R}\mathbf{1}>C \end{aligned}\tag{2}
μ=N1i=1∑NxiC=1−t×(0.98/MaxIt)Z=R2×IDX+R3⊗(∼IDX)IDX=R1>C(2)
猎物移动:
x
i
(
t
+
1
)
=
T
p
o
s
+
C
Z
c
o
s
(
2
π
R
4
)
×
(
T
p
o
s
−
x
i
(
t
)
)
(3)
x_{i}(t+1)=\boldsymbol{T}_{\mathrm{pos}}+\boldsymbol{CZ}cos(2\pi R4)\times(\boldsymbol{T}_{\mathrm{pos}}-\boldsymbol{x}_{i}(t))\tag{3}
xi(t+1)=Tpos+CZcos(2πR4)×(Tpos−xi(t))(3)
HPO的关键是猎人和猎物的身份选择,判断搜索代理以猎人或猎物的身份来进行信息更新:
x
i
(
t
+
1
)
=
{
x
i
(
t
)
+
0.5
[
(
2
C
Z
P
p
o
s
−
x
i
(
t
)
)
+
(
2
(
1
−
C
)
Z
μ
−
x
i
(
t
)
)
]
,
R
5
<
β
x
i
(
t
+
1
)
=
T
p
o
s
+
C
Z
c
o
s
(
2
π
R
4
)
×
(
T
p
o
s
−
x
i
(
t
)
)
,
o
t
h
e
r
w
i
s
e
(4)
\boldsymbol{x}_i(t+1)=\begin{cases}\boldsymbol{x}_i(t)+0.5[(2C\boldsymbol{Z}\boldsymbol{P}_{\mathrm{pos}}-\boldsymbol{x}_i(t))+(2(1-\boldsymbol{C})\boldsymbol{Z}\boldsymbol{\mu}-\boldsymbol{x}_i(t))],\boldsymbol{R}\boldsymbol{5}<\boldsymbol{\beta}\\\boldsymbol{x}_i(t+1)=\boldsymbol{T}_{\mathrm{pos}}+C\boldsymbol{Z}cos(2\pi R4)\times(\boldsymbol{T}_{\mathrm{pos}}-\boldsymbol{x}_i(t)),otherwise\end{cases}\quad\tag{4}
xi(t+1)={xi(t)+0.5[(2CZPpos−xi(t))+(2(1−C)Zμ−xi(t))],R5<βxi(t+1)=Tpos+CZcos(2πR4)×(Tpos−xi(t)),otherwise(4)
其中,R5是[0,1]内随机数,β为调节参数,值为0.2。如果R5<β,则将该搜索代理视为猎人,根据猎人捕猎机制更新位置;如果R5≥β,则将该搜索代理视为猎物,根据猎物移动机制更新位置。
流程图:
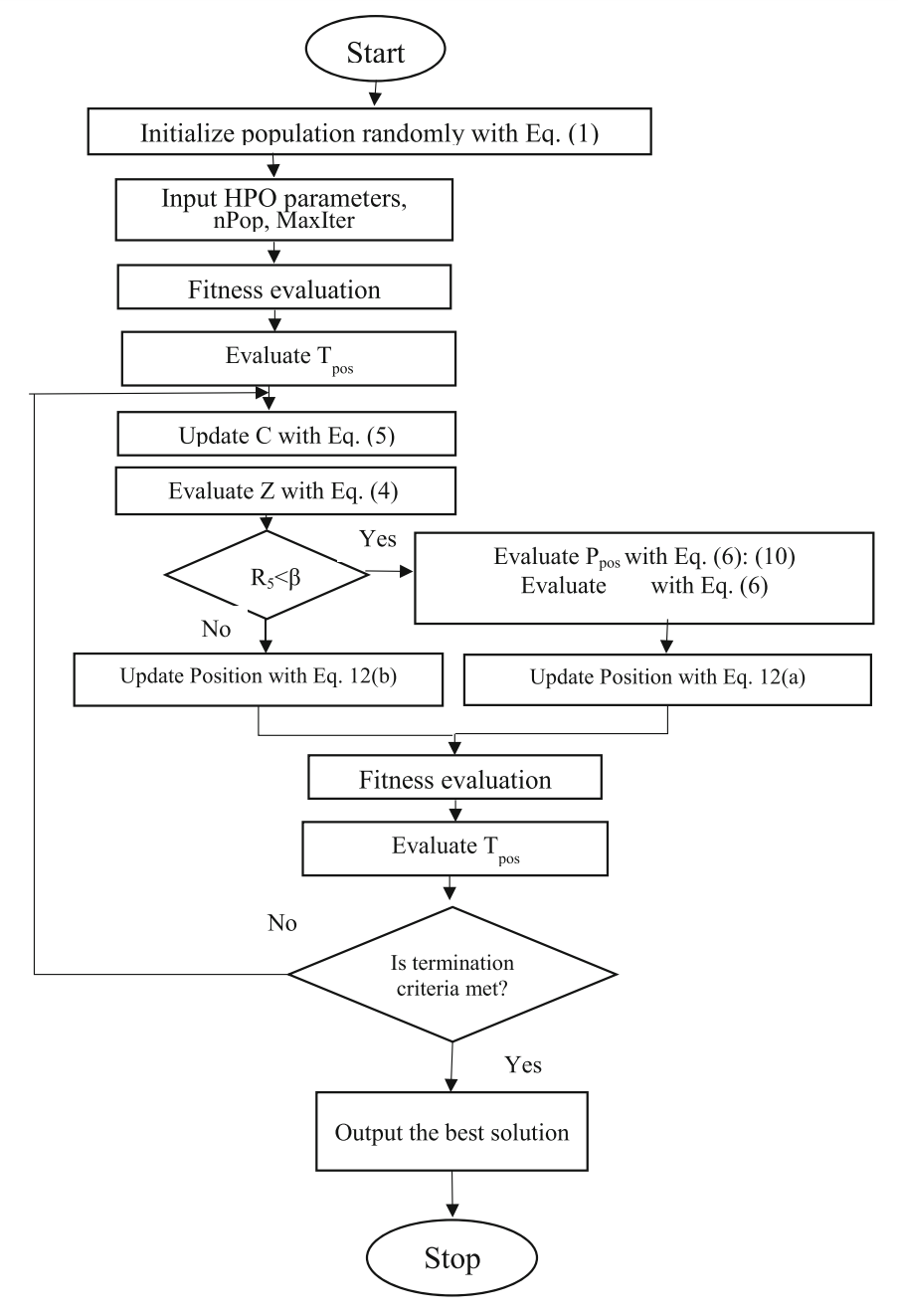
3.结果展示
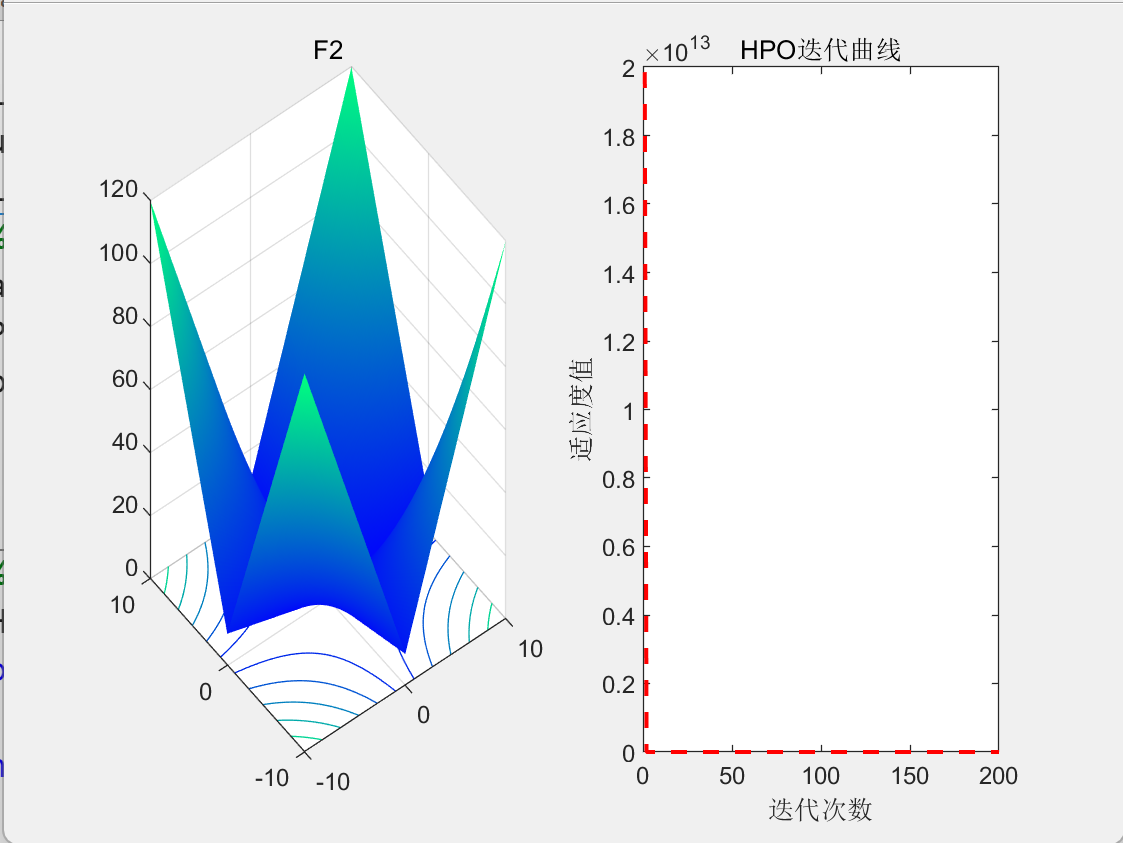
4.参考文献
[1] Naruei I, Keynia F, Sabbagh Molahosseini A. Hunter–prey optimization: Algorithm and applications[J]. Soft Computing, 2022, 26(3): 1279-1314.