题目

最大连续子序列求和，什么是连续最大子序列，先简单来说一个数组int a[]={-9,1,-10,2,3,4,-2,5,6,-2,-3}; 那它的连续最大子序列是2,3,4,-2,5,6 是18，就是使和最大的子序列。

算法

这个大概有几种想法，这里只介绍俩种。

遍历枚举

既然求连续最大的那我直接把所有的连续组合挨个求一次和最大的值比对，比他大就更新，结果就求出来了，算法复杂度是o($n^2$)

代码如下

#include<stdio.h>
int main()
{
	int a[]={-9,1,-10,2,3,4,-2,5,6,-2,-3};
	int count=sizeof(a)/sizeof(int);
	int sum=0;
	for(int i=0;i<count;i++)
	{
		int temp=0;
		for(int j=i;j<count;j++)
		{
			temp+=a[j];
			if(temp>sum)
			sum=temp;
		}
	}
	printf("sum=%d\n",sum);
	return 0;
 } 

优化版本

我们认真思考一下也没有可能直接优化成o(n)的算法呢，也就是说我们只遍历一次，就能解出结果。我们分析一下数据，从前一直往后加，如果加的当前已经为负值了，那还有必要继续加下去吗？没有必要了因为前面肯定是拖累，最大和肯定不会是包含前面和为负值的那些，那我们就重新计算和，即把计和变量归为0 重新计算再和最大值变量比更新最大值。

代码如下

#include<stdio.h>
int main()
{
	int a[]={-9,1,-10,2,3,4,-2,5,6,-2,-3};
	int count=sizeof(a)/sizeof(int);
	int sum=0,temp=0;
	for(int i=0;i<count;i++)
	{
		temp+=a[i];
		if(temp>sum)
		{
			sum=temp;
		}
		else if(temp<0)
		{
			temp=0;
		}
	    
	}
	printf("sum=%d\n",sum);
	return 0;
 } 

陈越姥姥题目

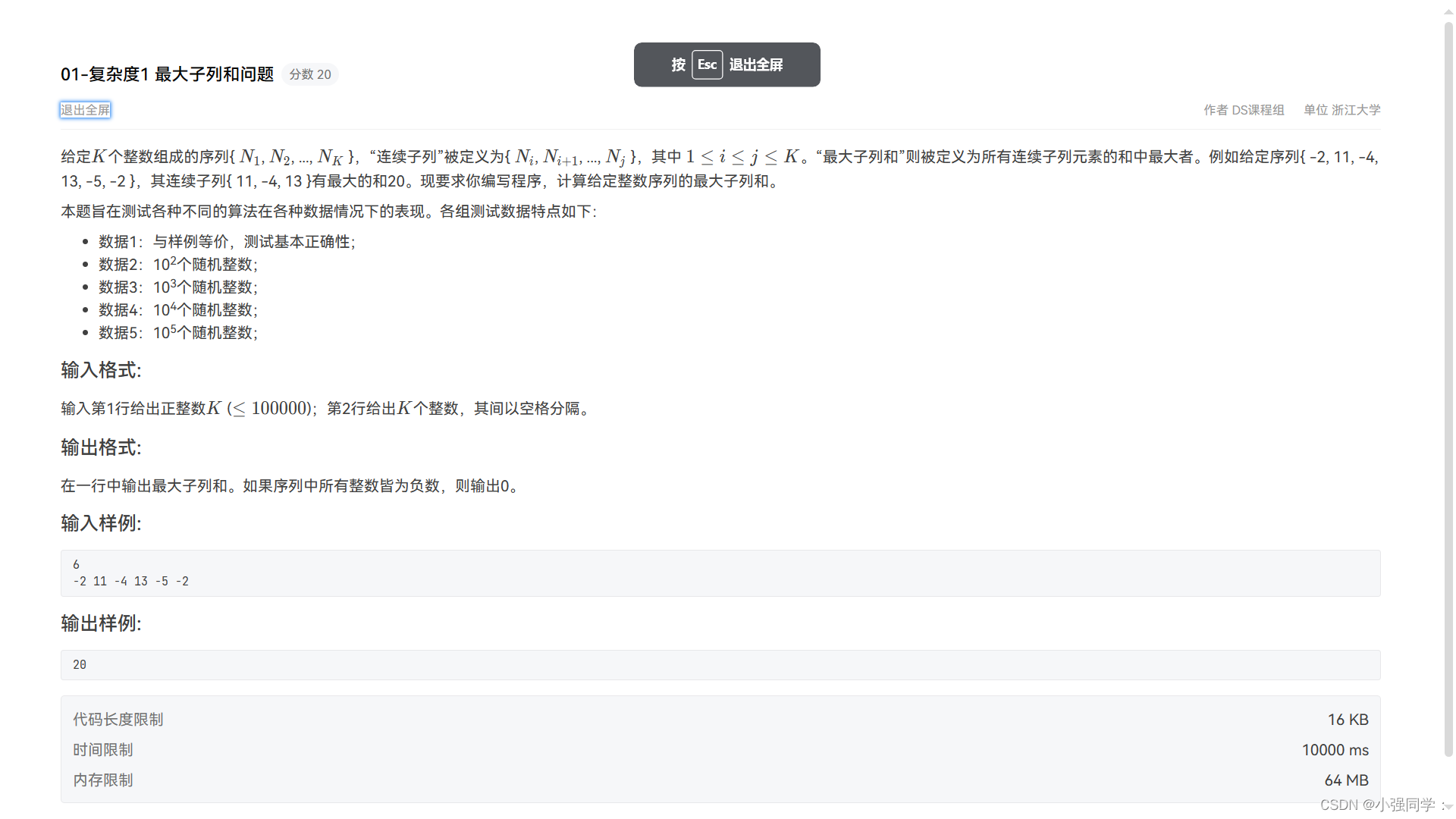
代码

#include<stdio.h>
int a[100001]; 
int main()
{
	int count;
	scanf("%d",&count);
	for(int i=0;i<count;i++)
	{
		scanf("%d",a+i);
	}
	int sum=0,temp=0;
	for(int i=0;i<count;i++)
	{
		temp+=a[i];
		if(temp>sum)
		{
			sum=temp;
		}
		else if(temp<0)
		{
			temp=0;
		}
	    
	}
	printf("%d\n",sum);
	return 0;
 }