上一篇：

【UE4 第一人称射击游戏】34-制作一个简易计时器

本篇效果：

可以看到击中目标后有了一个红色准心的提示效果

步骤：

1. 新建一个控件蓝图，命名为“Hitmarker”

双击打开“Hitmarker”，拖入一个图像控件，锚点设置为正中间

尺寸设置为32×32

位置设置为（-16，-16），让这个图像在屏幕正中间

添加一个动画，命名为“Fade”

选中“Fade”，添加一个轨迹

添加一个对 颜色和不透明度的控制，设置第0s时Alpha为1，设置第0.25s时Alpha为0，设置第0.5s时Alpha为1.

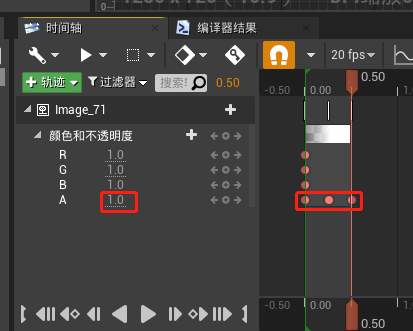
动画效果如下：（有个淡入淡出的效果）

如果感觉不明显，可以将颜色改为红色

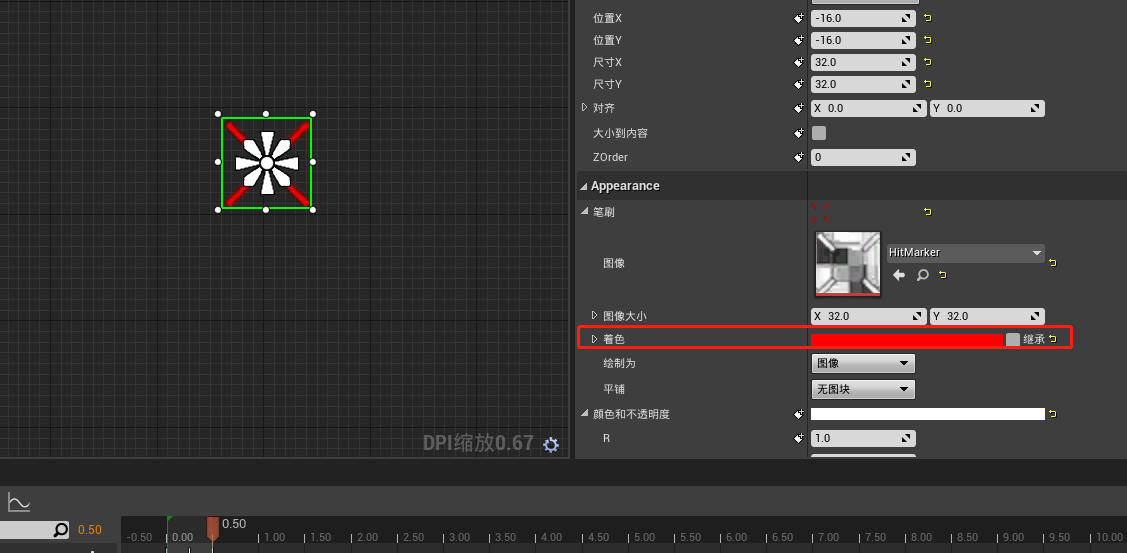
在图表中添加如下节点：

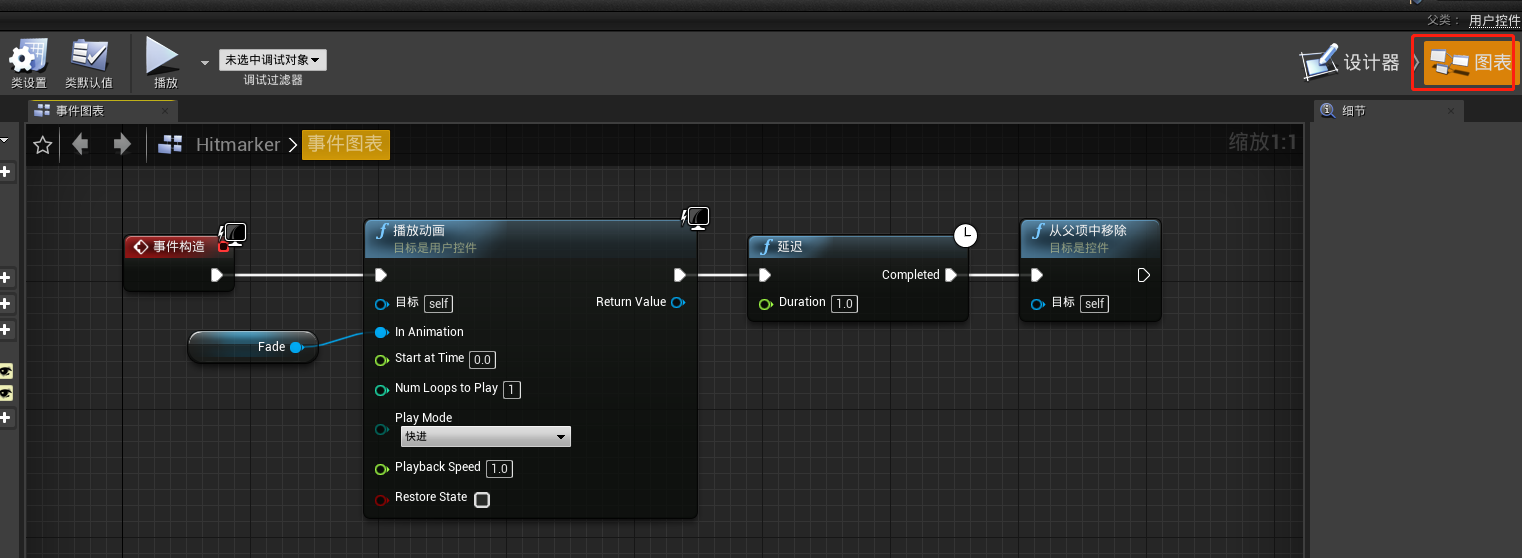
接下来想做的是当击中敌人后，能够播放这个UI动画

2. 打开“SimpleAI”，删除AI被击中时打印字符串的节点

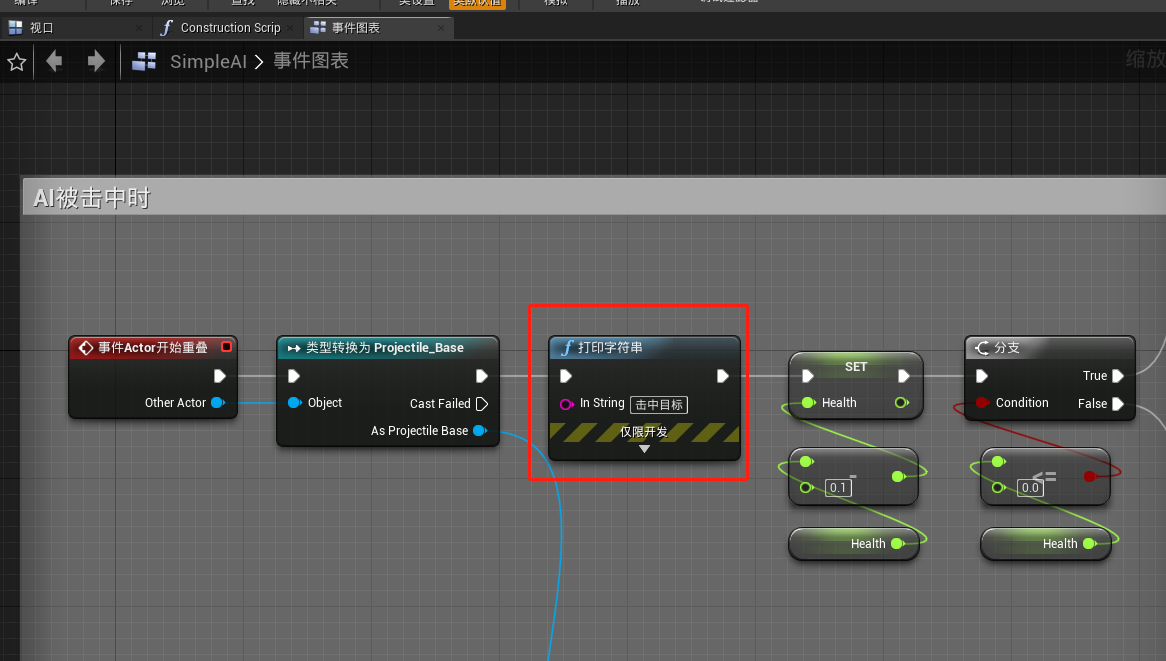
替换为如下节点：

运行游戏效果如文章开头所示。