题目解析

15. 三数之和

这道题有两个需要注意的地方：1. 三个数字也不可以是同一个位置上的 2. 最终结果里面的三元组不可以是重复的

所以这道题就需要对结果实现去重这一个逻辑，遇到相同的数字就需要往后面移动，忽略

---

算法讲解

1. 首先对数组进行排序

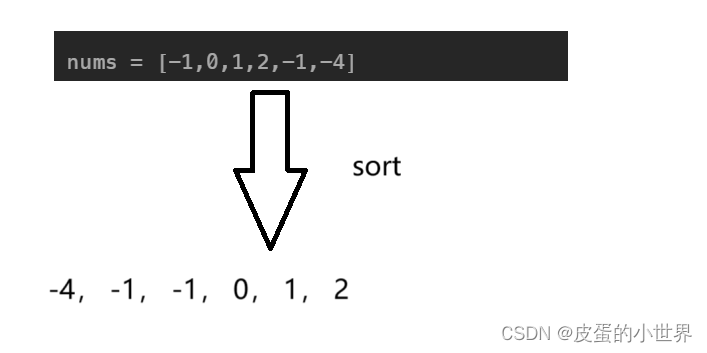
对数组进行排序之后，我们就可以使用上一道题"两数之和"的算法思想，在有序区间里面寻找两个数字之和 == target的二元组，但是我们这里是三元组，使用双指针只能寻找两个数字。因此我们可以确定一个数字，在剩下的区间中寻找target == 0 - 确定的数字，所以这样这道题就转化为寻找target二元组（还需要去重！！！）

2. 完成三元组问题转化为二元组的实现

3. 完成去重

1. 首先需要对left 和 right 指针进行去重，寻找到nums[left] + nums[right] == target的时候，两个指针可以一起向中心移动一步，这个时候就需要对对撞指针进行去重了，因为如果移动之后的指针还是移动之前的值的话，那么最终出来的三元组还是上一个，放在最终结果里面肯定不可以
2. 其次还是需要对当前确定的这个数字进行去重，道理同上面对撞指针的原理一样

//对i去重
if(i != 0 && nums[i] == nums[i-1]) continue;


//对 双指针 去重
while(left < right && nums[left - 1] == nums[right])
{
	left++;
}
while(right > left && nums[right + 1] == nums[right])
{
	right--;
}

---

代码编写

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        //先给数组排序
        sort(nums.begin(), nums.end());
        vector<vector<int>> ret;
        int n = nums.size();
        //确定一个数字 寻找其他区间的两数之和
        for(int i = 0; i < n; i++)
        {
            if(nums[i] > 0) break;
            //对i去重
            if(i != 0 && nums[i] == nums[i-1]) continue;
            int left = i + 1;
            int right = n - 1;
            int target = 0 - nums[i];  //寻找两数之和的target
            while(left < right)
            {
                if(nums[left] + nums[right] == target)
                {
                    ret.push_back({nums[left], nums[right], nums[i]});
                    left++;
                    right--;
                    //对 双指针 去重
                    while(left < right && nums[left - 1] == nums[right])
                    {
                        left++;
                    }
                    while(right > left && nums[right + 1] == nums[right])
                    {
                        right--;
                    }
                }
                else if(nums[left] + nums[right] > target)
                {
                    right--;
                }
                else left++;
            }
        }
        return ret;
    }
};

---