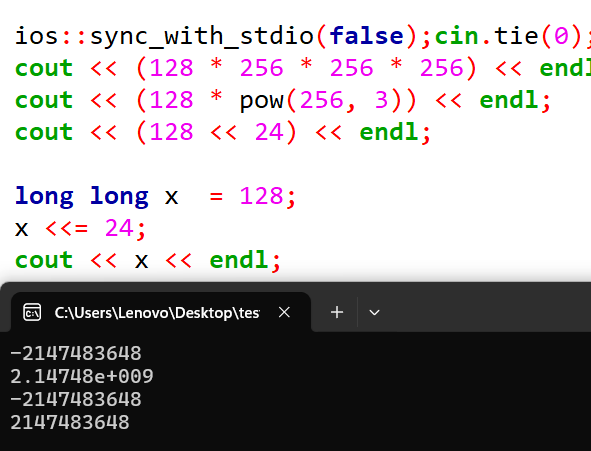
例题一

解法(快排思想 - 三指针法使数组分三块):
算法思路:
类⽐数组分两块的算法思想,这⾥是将数组分成三块,那么我们可以再添加⼀个指针,实现数组分
三块。
设数组⼤⼩为
n
,定义三个指针
left, cur, right
:
◦
left :⽤来标记
0
序列的末尾,因此初始化为
-1
;
◦
cur :⽤来扫描数组,初始化为
0
;
◦
right :⽤来标记
2
序列的起始位置,因此初始化为
n
。
在 cur 往后扫描的过程中,保证:
◦
[0, left] 内的元素都是
0
;
◦
[left + 1, cur - 1] 内的元素都是
1
;
◦
[cur, right - 1] 内的元素是待定元素;
◦
[right, n] 内的元素都是
2
。
算法流程:
a.
初始化 cur = 0
,
left = -1
,
right = numsSize
;
b.
当 cur < right
的时候(因为
right
表⽰的是
2
序列的左边界,因此当
cur
碰到 right 的时候,说明已经将所有数据扫描完毕了),⼀直进⾏下⾯循环:
根据 nums[cur]
的值,可以分为下⾯三种情况:
i.
nums[cur] == 0 ;说明此时这个位置的元素需要在 left + 1 的位置上,因此交 换 left + 1
与
cur
位置的元素,并且让
left++ (指向 0 序列的右边界),
cur++
(为什么可以
++
呢,是因为
left + 1
位置要么是 0 ,要么是 cur
,交换 完毕之后,这个位置的值已经符合我们的要求,因此 cur++ );
ii.
nums[cur] == 1 ;说明这个位置应该在
left
和
cur 之间,此时⽆需交换,直接让 cur++
,判断下⼀个元素即可;
iii.
nums[cur] == 2
;说明这个位置的元素应该在
right - 1
的位置,因此交换 right - 1 与
cur
位置的元素,并且让
right--
(指向
2
序列的左边界),cur 不变(因为交换过来的数是没有被判断过的,因此需要在下轮循环中判断)
c.
当循环结束之后: [0, left] 表⽰
0
序列; [left + 1, right - 1] 表⽰ 1 序列; [right, numsSize - 1]
表⽰ 2 序列。

例题二

解法(数组分三块思想 + 随机选择基准元素的快速排序):
算法思路:
我们在数据结构阶段学习的快速排序的思想可以知道,快排最核⼼的⼀步就是 Partition (分割数
据):将数据按照⼀个标准,分成左右两部分。
如果我们使⽤荷兰国旗问题的思想,将数组划分为 左 中 右 三部分:左边是⽐基准元素⼩的数据,
中间是与基准元素相同的数据,右边是⽐基准元素⼤的数据。然后再去递归的排序左边部分和右边
部分即可(可以舍去⼤量的中间部分)。
在处理数据量有很多重复的情况下,效率会⼤⼤提升。
算法流程:
随机选择基准算法流程:
函数设计:int randomKey(vector<int>& nums, int left, int right)
a.
在主函数那⾥种⼀颗随机数种⼦;
b.
在随机选择基准函数这⾥⽣成⼀个随机数;
c.
由于我们要随机产⽣⼀个基准,因此可以将随机数转换成随机下标:让随机数 % 上区间⼤⼩,
然后加上区间的左边界即可。
快速排序算法主要流程:
a.
定义递归出⼝;
b.
利⽤随机选择基准函数⽣成⼀个基准元素;
c.
利⽤荷兰国旗思想将数组划分成三个区域;
d.
递归处理左边区域和右边区域。

例题三

解法(快速选择算法):
算法思路:
在快排中,当我们把数组「分成三块」之后:
[l, left] [left + 1, right - 1] [right, r] ,我们可以通过计算每⼀个区间内元素的「个数」,进⽽推断出我们要找的元素是在「哪⼀个区间」⾥⾯。
那么我们可以直接去「相应的区间」去寻找最终结果就好了。

例题四

路: 在快排中,当我们把数组「分成三块」之后: [l, left] [left + 1, right - 1] [right, r] ,我们可以通过计算每⼀个区间内元素的「个数」,进⽽推断出最⼩的 k 个数在哪 些区间⾥⾯。 那么我们可以直接去「相应的区间」继续划分数组即可。