超时重传时间的选择是 TCP 最复杂的问题之一
1、超时重传时间RTO的选取
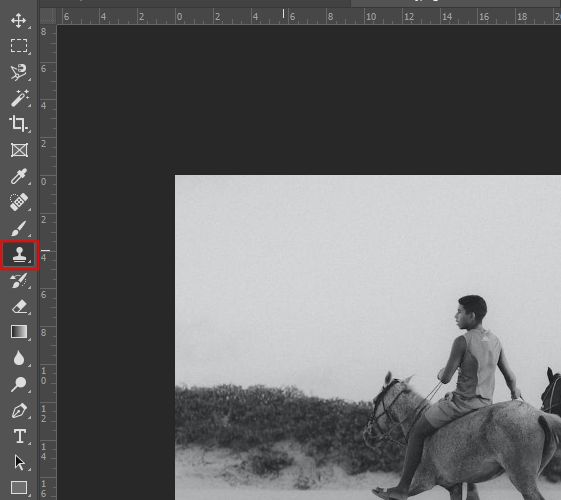
假设主机 A 给主机 B 发送 TCP 数据报文段
0
0
0,并记录下当前的时间
主机 B 收到后,给主机 A 发送相应的确认报文段
主机 A 收到确认报文段后,记录下当前的时间
那么主机 A 记录的这两个时间,它们的差值就是报文段的往返时间 RTT
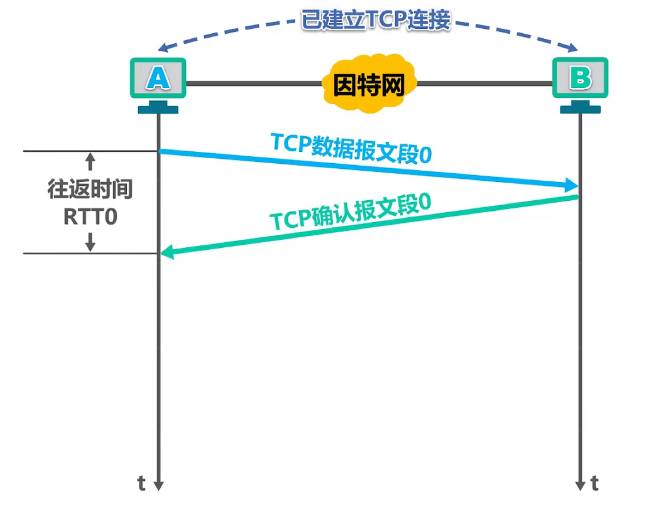
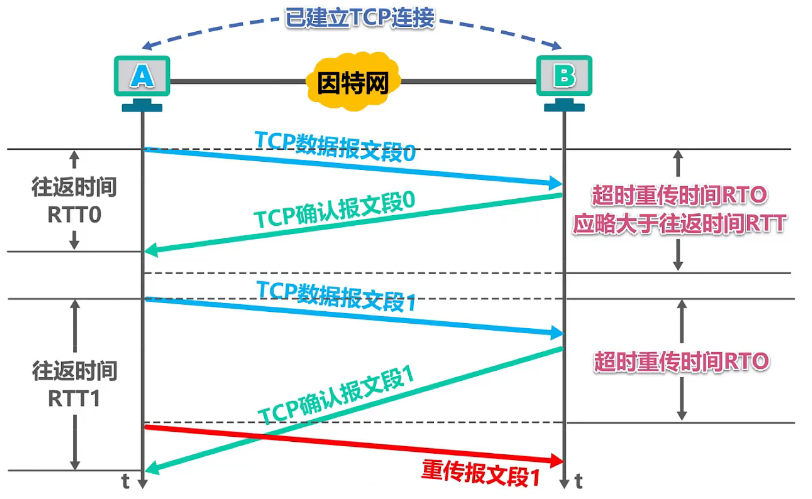
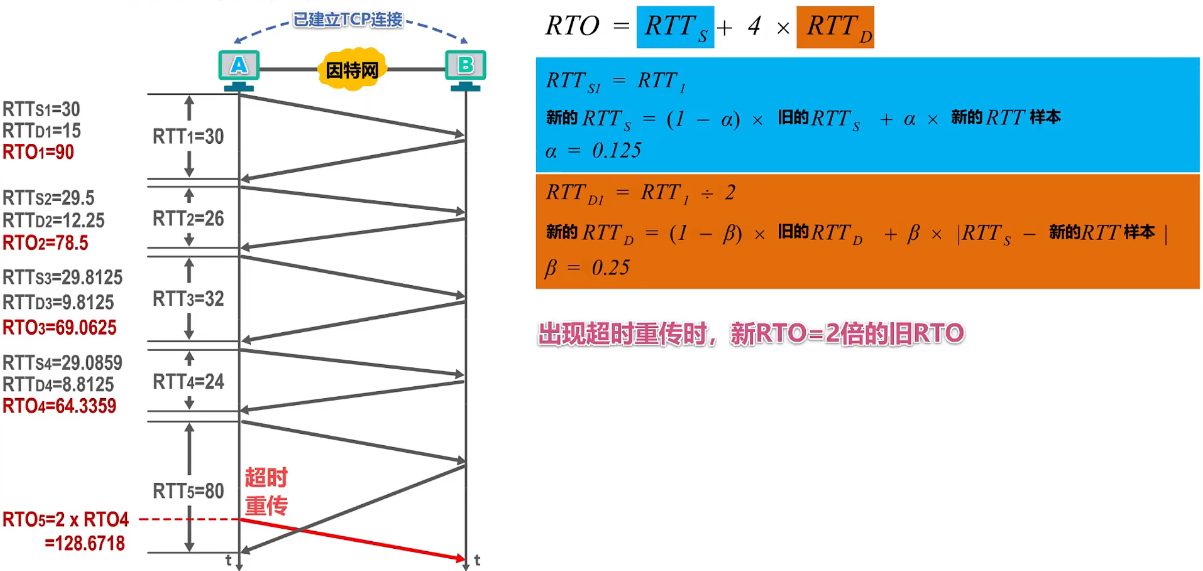
若把超时重传时间 RTO 的时间设置为比 RTT0 的时间小会怎样呢
很显然,这会引起报文段比必要的重传,是网络负荷增大
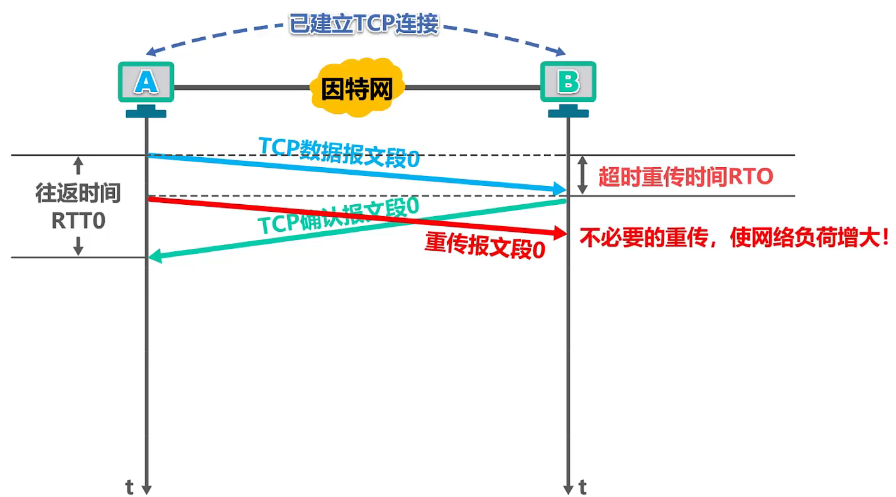
若把超时重传时间 RTO 的时间设置远大于i RTT0 的值呢?
很显然,这会使重传推迟的时间增长,使网络的空闲的时间增大,降低了传输效率
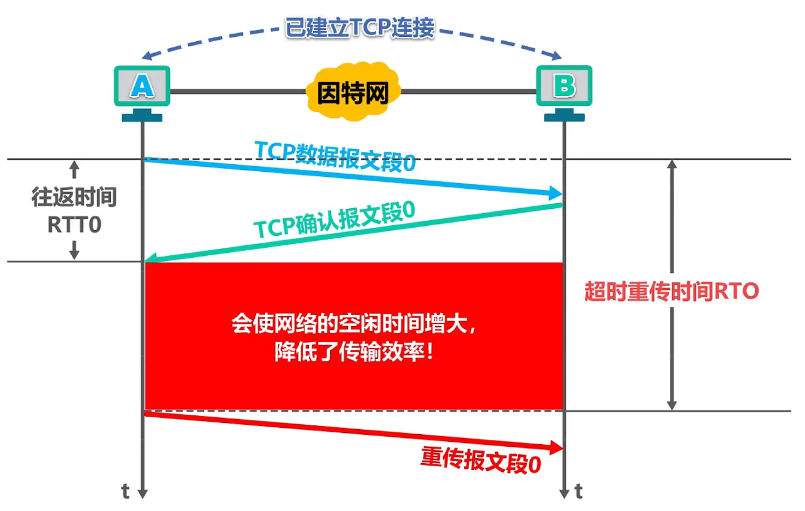
综上以上两种情况,超时重传时间 RTO 的值应略大于往返时间 RTT
然而,TCP 下层是复杂的互联网环境
主机 A 所发送的报文段可能只经过一个高速率的局域网,也有可能经过多个低速率的网络
- 并且,每个
IP数据报的转发路由还可能不同
如下所示,
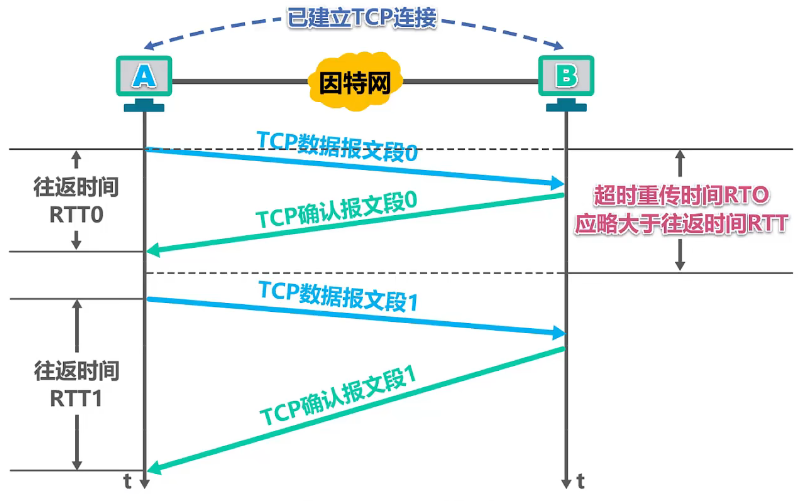
显然,RTT1 远大于 RTT0,若超时重传时间 RTO 还是之前所确定的略大于 RTT0 的话
- 这对数据报文段 1 1 1 是不合适的,会造成该报文段不必要的重传
2、RTO的计算(加权平均往返时间RTTs & RTT 偏差的加权平均 RTTD)
不能直接使用某次测量得到的 RTT 样本来计算超时重传时间 RTO \color{red}不能直接使用某次测量得到的\texttt{RTT}样本来计算超时重传时间 \texttt{RTO} 不能直接使用某次测量得到的RTT样本来计算超时重传时间RTO。
利用每次测量得到的 RTT 样本,计算
加权平均往返时间
RTTs
\color{red}加权平均往返时间\texttt{RTTs}
加权平均往返时间RTTs(又称为平滑的往返时间)。
当测量到第一个 RTT 样本时,RTTs 的值直接取为第一个 RTT 的值
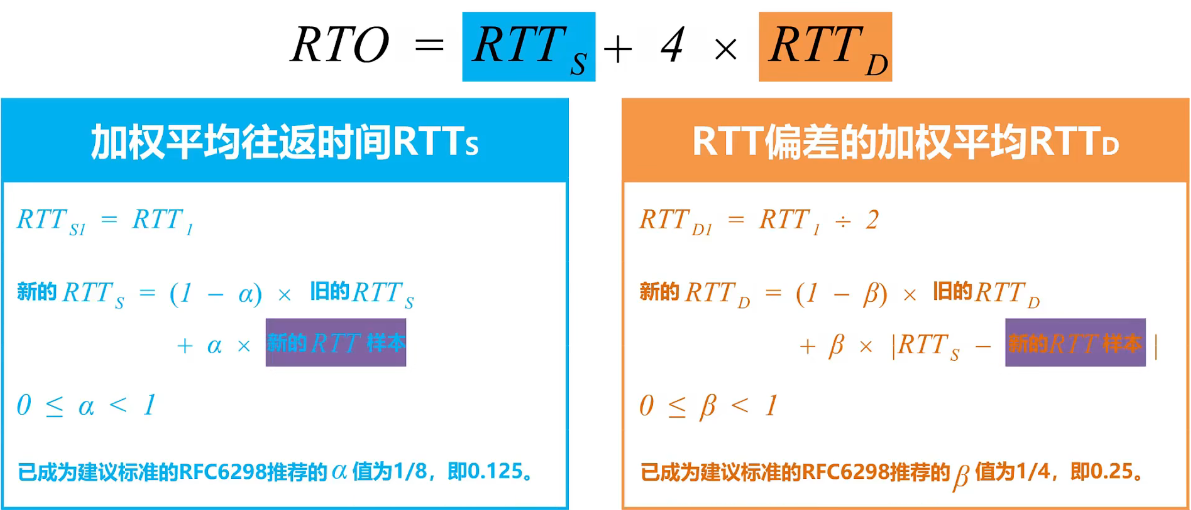
- RTT S1 = RTT 1 \color{red}\texttt{RTT}_{\texttt{S1}} = \texttt{RTT}_{\texttt{1}} RTTS1=RTT1
以后每测量一个 RTT 样本时,都按该公式来计算新的 RTTs 的值
-
新的 RTTs = ( 1 − α ) × 旧的 RTTs + α × 新的 RTT 样本 \color{red}新的 \texttt{RTTs} = (1-\alpha) \times 旧的 \texttt{RTTs} + \alpha \times 新的\texttt{RTT}样本 新的RTTs=(1−α)×旧的RTTs+α×新的RTT样本
在上式中。 0 ≤ α < 1 : 0 \le \alpha < 1: 0≤α<1:
若 α \alpha α 很接近于 0 0 0,则新
RTT样本对RTTs的影响不大 若 α \alpha α 很接近于 1 1 1,则新
RTT样本对RTTs的影响较大已成为建议标准的
RFC6298推荐的 α \alpha α 值为 1 / 8 1/8 1/8 ,即 0.125 0.125 0.125
用这种方法得出的加权平均往返时间 RTTs 就比测量出的 RTT 值更加平滑。
显然,超时重传时间 RTO 应略大于加权平均往返时间 RTTs 。
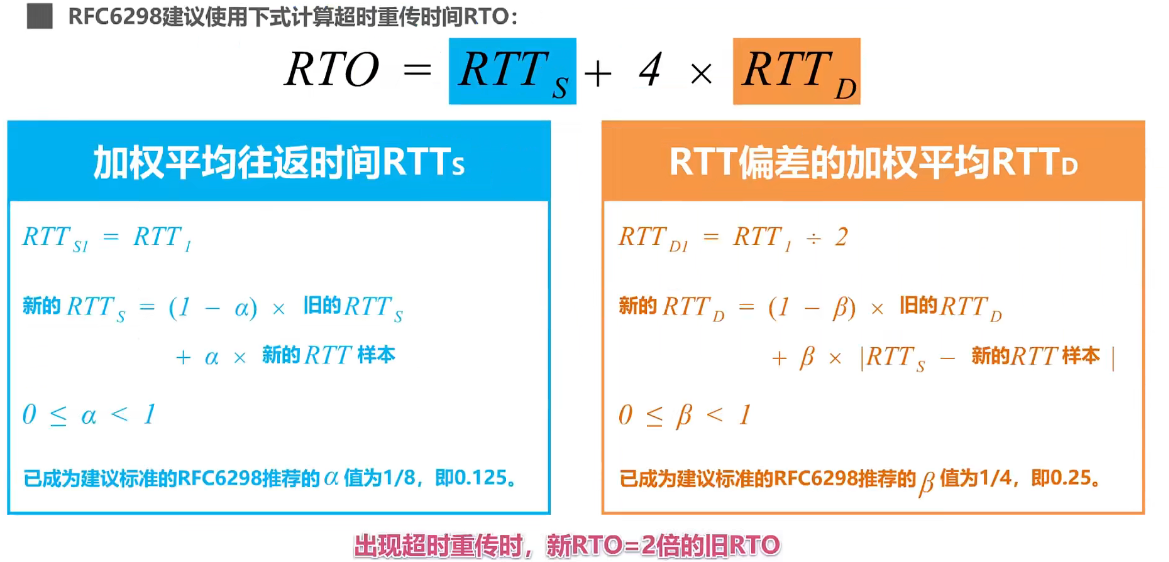
RFC6298 建议使用下式计算超时重传时间 RTO:
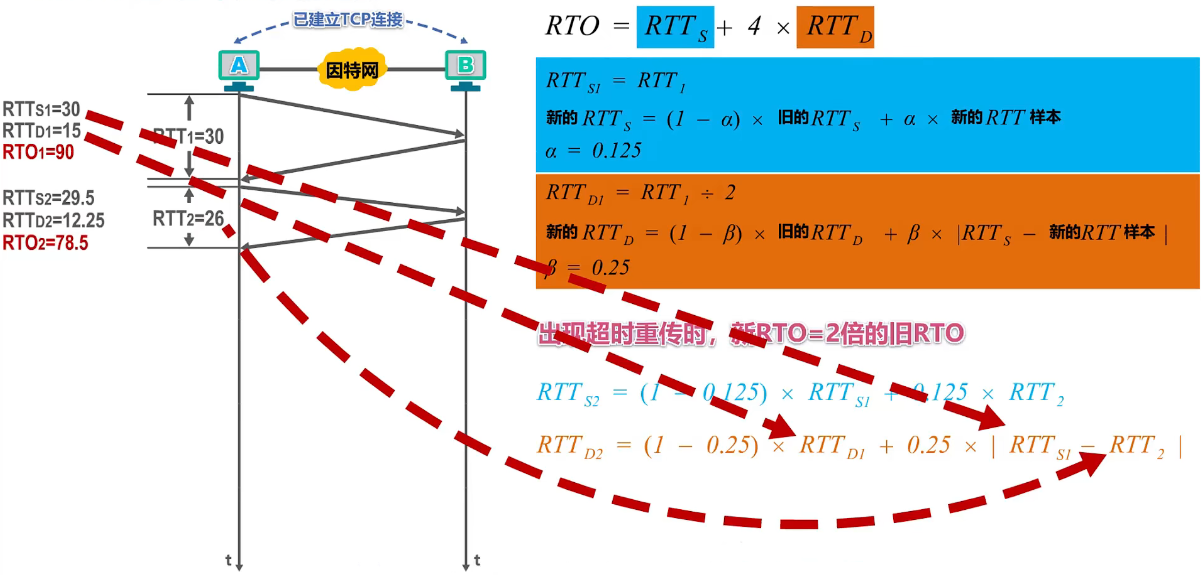
- RTO = RTTs + 4 × RTT D \color{red}\texttt{RTO} = \texttt{RTTs} + 4 \times \texttt{RTT}_{\texttt{D}} RTO=RTTs+4×RTTD
其中 RTT D \texttt{RTT}_{\texttt{D}} RTTD : RTT \texttt{RTT} RTT 偏差的加权平均 RTT D \texttt{RTT}_{\texttt{D}} RTTD
- RTT D1 = RTT 1 / 2 \color{red}\texttt{RTT}_{\texttt{D1}} = \texttt{RTT}_{\texttt{1}} / 2 RTTD1=RTT1/2
新的 RTT D = ( 1 − β ) × 旧的 RTT D + β × ∣ RTTs − 新的 RTT 样本 ∣ \color{red}新的 \texttt{RTT}_{\texttt{D}} = (1-\beta) \times 旧的 \texttt{RTT}_{\texttt{D}} + \beta \times|\texttt{RTTs} -新的\texttt{RTT}样本| 新的RTTD=(1−β)×旧的RTTD+β×∣RTTs−新的RTT样本∣
在上式中。 0 ≤ β < 1 : 0 \le \beta< 1: 0≤β<1:
已成为建议标准的 RFC6298 推荐的
β
\beta
β 值为
1
/
4
1/4
1/4 ,即
0.25
0.25
0.25
从上述发现,不管是 RTTs 还是 RTTD,都是基于所测量到的 RTT 样本测量到的
若所测量到的 RTT 样本不正确,那么所计算出的 RTTs 和 RTTD 自然就不正确
进而所计算出的超时重传时间 RTO 也就不正确
3、往返时间 RTT 的测量
往返时间 RTT 的测量比较复杂
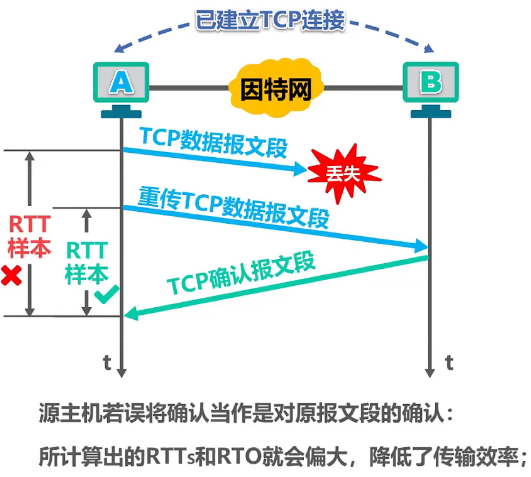
3.1、TCP数据报文段丢失
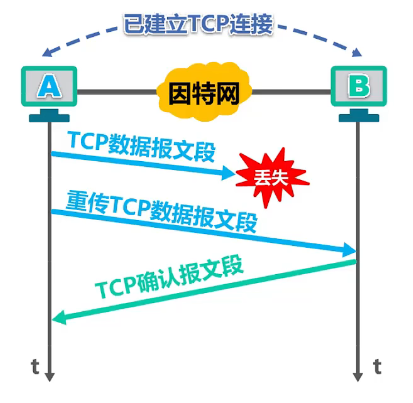
对于上述所示,主机 A 收到该确认报文段后
- 无法判断该报文段是对原报文段的确认还是对重传报文段的确认
该报文段实际上是对重传报文段的确认
- 也就是说正确的
RTT应该是这一段时间(绿色✔标记)
但是若主机 A 误将该确认当作是对原报文段的确认
- 也就是误认这段时间
RTT(红色❌标记)
则所计算出的 RTTs 和 RTO 就会偏大,降低了传输效率
3.2、迟到的确认报文段
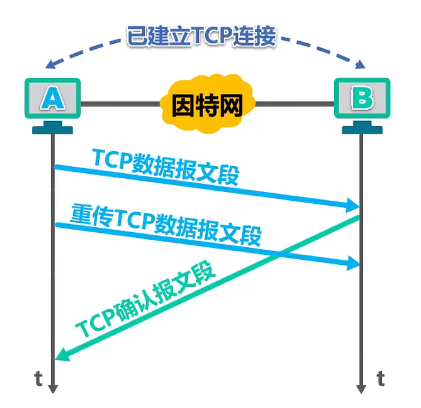
如上所示:该确认报文段没有在正常时间内到达主机 A,这必然会导致主机 A 对之前所发送的数据报文段的超时重传
主机 A 收到迟到的确认报文段后
- 无法判断该报文段是对原报文段的确认还是对重传报文段的确认
该报文段实际上是对原报文段的确认
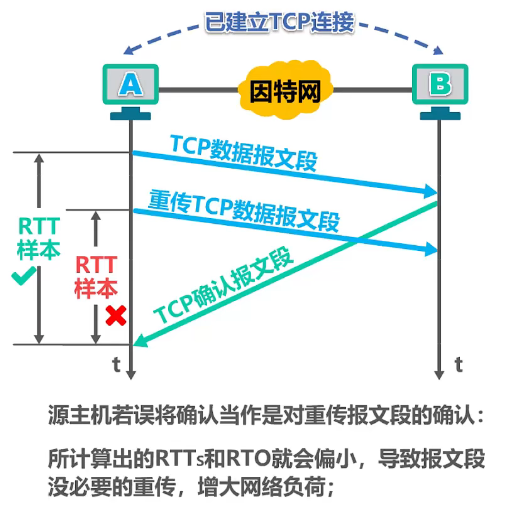
- 也就是说正确的
RTT应该是这一段时间(绿色✔标记)
但是若主机 A 误将该确认当作是对重传报文段的确认
- 也就是误认这段时间
RTT(红色❌标记)
则所计算出的 RTTs 和 RTO 就会偏小,这会导致报文段没有必要的重传,增大网络负荷。
从上述可以看出,当发送方出现超时重传后,收到确认报文段时,是无法判断该报文段是对原报文段的确认还是对重传报文段的确认
- 也就是无法准确测量
RTT,进而无法正确计算超时重传时间RTO
4、karn 算法及改进
针对 出现超时重传时无法测准往返时间 RTT \color{blue}出现超时重传时无法测准往返时间\texttt{RTT} 出现超时重传时无法测准往返时间RTT的问题, K a r n \color{red}Karn Karn 提出了一个 算法 \color{red}算法 算法:
- 在计算加权平均往返时间 RTTs 时,只要报文段重传了,就不采用其往返时间 RTT 样本。 \color{red}在计算加权平均往返时间\texttt{RTTs}时,只要报文段重传了,就不采用其往返时间\texttt{RTT}样本。 在计算加权平均往返时间RTTs时,只要报文段重传了,就不采用其往返时间RTT样本。
就是出现重传时,不重新计算 RTTs ,进而超时重传时间 RTO 也不会重新计算。
-
这又引起了新的问题。设想出现这样的情况:报文段的时延突然增大了很多,并且之后很长一段时间都会保持这种时延。因此在原来得出的重传时间内,不会收到确认报文段。于是就重传报文段。
但根据
Karn算法,不考虑重传的报文段的往返时间样本。这样,超时重传时间就无法更新。这会导致报文段反复被重传。
因此,要对 K a r n 算法进行修正 \color{red}Karn算法进行修正 Karn算法进行修正。方法是:
- 报文段每重传一次,就把超时重传时间 RTO 增大一些 \color{red}报文段每重传一次,就把超时重传时间\texttt{RTO}增大一些 报文段每重传一次,就把超时重传时间RTO增大一些。
- 典型的做法是将新
RTO的值取为旧RTO值的 2 2 2 倍。
5、TCP超时重传时间的计算
6、小结






![[L1 - 5分合集]心理阴影面积](https://img-blog.csdnimg.cn/6ab8e13b637540d28dffdd298a21e221.jpeg#pic_center)