1. 题目解析

题目地址：点这里

2. 讲解算法原理

方法一：

1. 首先，定义一个大小为n+1的数组dp，用于存储到达每个台阶的最小花费。其中n为cost数组的大小，也就是楼梯的总数。

2. 初始化dp数组的前两个元素dp[0]和dp[1]为0，表示初始状态下到达第一个台阶和第二个台阶的最小花费为0。

3. 然后，从第三个台阶开始循环遍历到第n个台阶。对于每个台阶i，计算两种方式到达该台阶的最小花费：一种是从前一个台阶i-1跳上来，另一种是从前前个台阶i-2跳上来。分别计算出这两种方式的花费，取其中较小的一个作为到达当前台阶i的最小花费，将其赋值给dp[i]。

4. 最后，返回dp[n]，表示到达第n个台阶的最小花费。

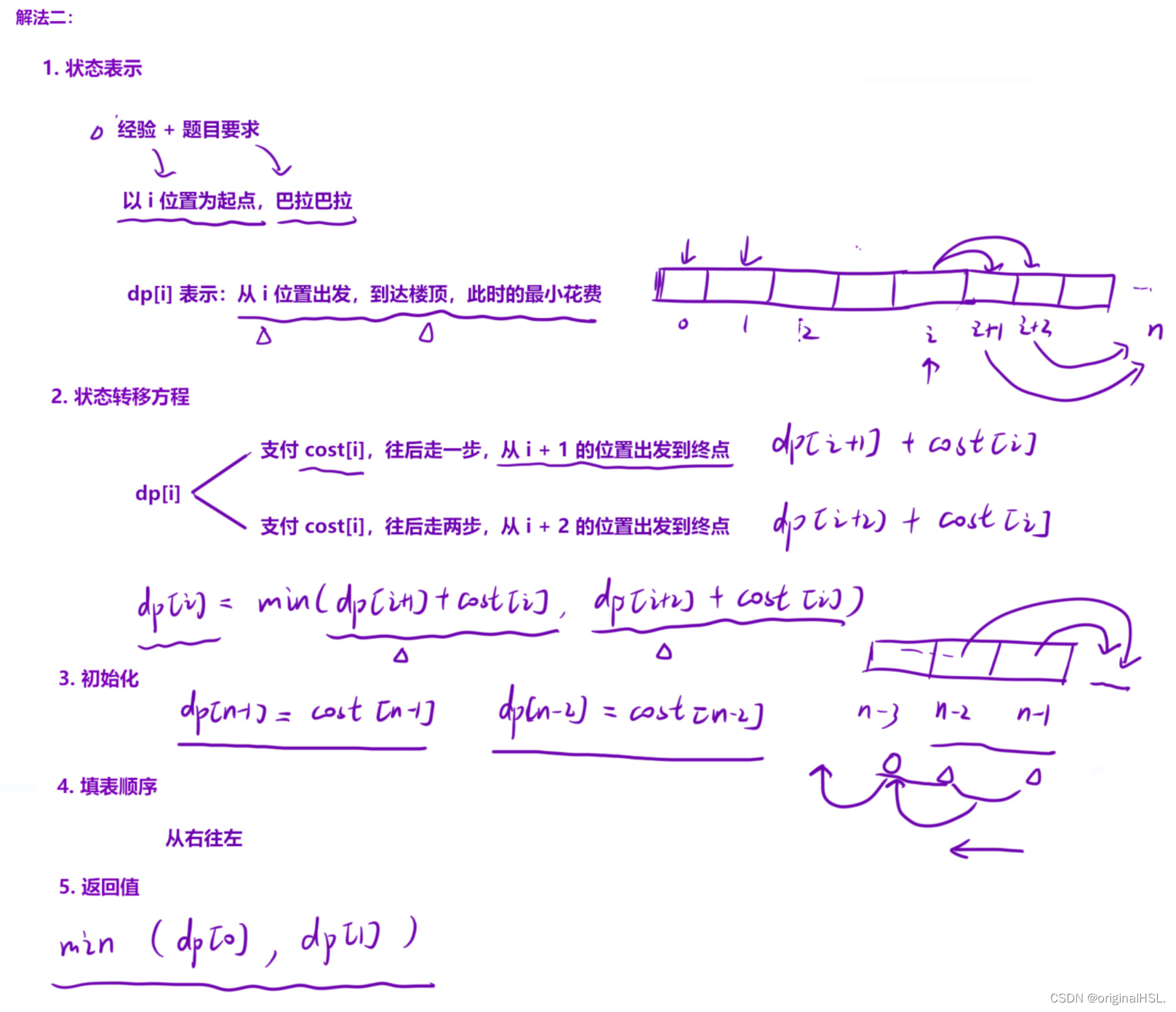
方法二：

1. 首先，定义一个大小为n的数组dp，用于存储到达每个台阶的最小花费。其中n为cost数组的大小，也就是楼梯的总数。

2. 接下来，初始化dp数组的最后两个元素dp[n-1]和dp[n-2]为cost[n-1]和cost[n-2]，分别表示到达最后一个台阶和倒数第二个台阶的最小花费。

3. 然后，从倒数第三个台阶开始循环遍历到第一个台阶。对于每个台阶i，计算两种方式到达该台阶的最小花费：一种是从下一个台阶i+1跳上来，另一种是从下下个台阶i+2跳上来。分别计算出这两种方式的花费，取其中较小的一个作为到达当前台阶i的最小花费，将其赋值给dp[i]。

4. 最后，返回dp[0]和dp[1]中较小的一个，表示从第一个台阶和第二个台阶中选择一个起点的最小花费。

3. 编写代码

解法一

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();
        vector<int> dp(n+1);
        dp[0]=0,dp[1]=0;
        for(int i=2;i<=n;i++)
        {
            int a=dp[i-1]+cost[i-1];
            int b=dp[i-2]+cost[i-2];
            dp[i]=a>b?b:a;
        }
        return dp[n];
    }
};

解法二

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();
        vector<int> dp(n);
        dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];
        for(int i=n-3;i>=0;i--)
        {
            int a=dp[i+1]+cost[i];
            int b=dp[i+2]+cost[i];
            dp[i]=a>b?b:a;
        }
        return min(dp[0],dp[1]);
    }
};