目录

问题：给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。

2.简单实现一个位图 

 3.如何利用位图求两个集合的交集、并集

---

问题：给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。

1. 40亿个不重复的无符号整数需要多少空间：大概16G；那么使用哈希或者是红黑树内存不够；
2. 可以直接遍历，时间复杂度O(N)；
3. 排序时间复杂O(logN)，二分查找时间复杂度O(longN)；

Q：效率都不太好，有没有更好办法呢？

A：让一个比特位来标记一个元素存在或者不存在

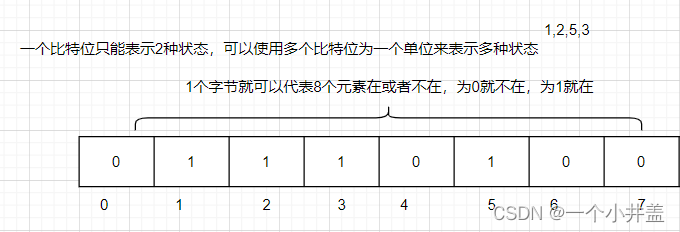
40个整形放在位图里面只需要0.5G，而且查找的时间复杂度：O(1)，非常棒；

2.简单实现一个位图 

位图的概念：所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

1. 初始化+1是为了：除了之后有余数，需要多开一个单位来存放，
2. 大小端对于位图没有影响

 

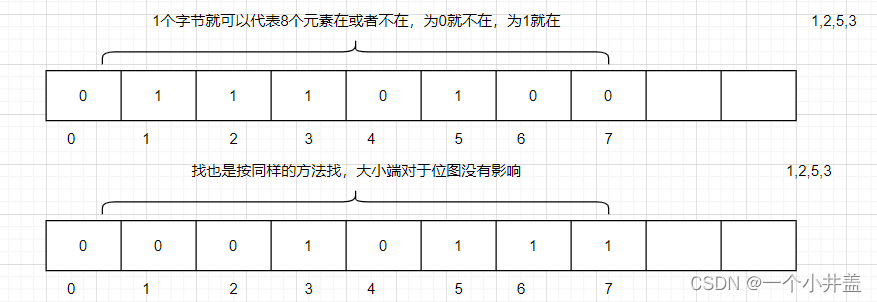
template<size_t N>
	class bitset
	{
	public:
		bitset()
		{
			_bits.resize(N / 8 + 1, 0);
		}

		void set(size_t x)//把状态改为存在
		{
			//看在哪一个字节里面
			size_t i = x / 8;
			//第几位
			size_t j = x % 8;
			//大小端没有区别，找也是按这种方法找
			_bits[i] |= (1 << j);
		}

		void reset(size_t x)//把状态改为不存在
		{
			size_t i = x / 8;
			size_t j = x % 8;

			_bits[i] &= (~(1 << j));
		}

		bool test(size_t x)//查询是否存在
		{
			size_t i = x / 8;
			size_t j = x % 8;

			return _bits[i] & (1 << j);
		}

	private:
		std::vector<char> _bits;
	};

 3.如何利用位图求两个集合的交集、并集

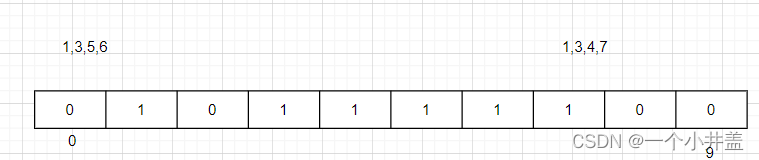
1.并集

• 把两个集合的元素都插入在一个位图里面，然后遍历一遍判断在不在即可；

 

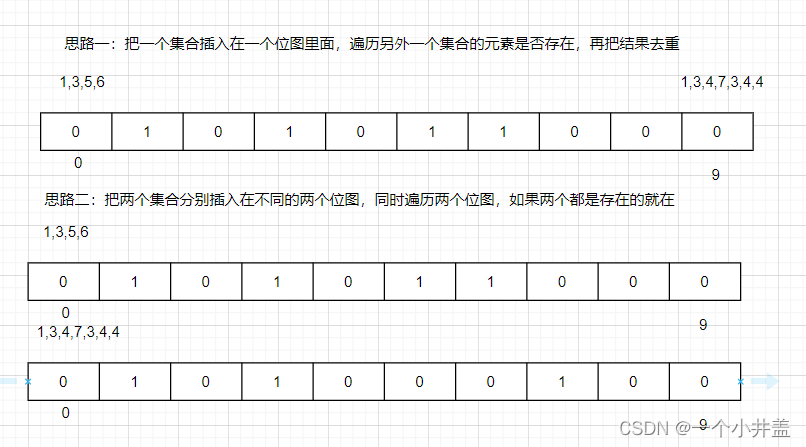
 2.交集

• 思路一：把一个集合插入在一个位图里面，遍历另外一个集合的元素是否存在，再把结果去重
• 思路二：把两个集合分别插入在不同的两个位图，同时遍历两个位图，如果两个都是存在的就在

 

总结一下：位图的可以做些什么？

A：1. 快速查找某个数据是否在一个集合中 2. 排序（全部插入，遍历一遍） 3. 求两个集合的交集、并集等