【Godot4.2】2D辅助类Geometry2D入门

news2024/9/30 9:24:38

概述

Godot4.2提供了一个名叫Geometry2D的类。它提供了一些用于2D几何图形如多边形（Polygon）、折线（PolyLine）相关的函数，可以方便实现诸如多边形与多边形或多边形与折线的布尔运算、求交点等。

这是一个非常强大的2D几何辅助类，可以方便你基于几何图形的一些复杂操作。

本篇是笔者2023年7月受到B站一个搬运视频启发，然后基于Godot内置文档研究Geometry2D并逐个尝试方法，从而总结的一份笔记。原始笔记分为两篇，这里合二为一，并可能会做一定的改写和扩充。期望对你的学习或项目有用。

参考视频

  • 【转载】【Godot】最被低估的(几何类)工具 - The MOST UNDERRATED Godot tool (GEOMETRY CLASS)】

多边形与多边形的布尔运算

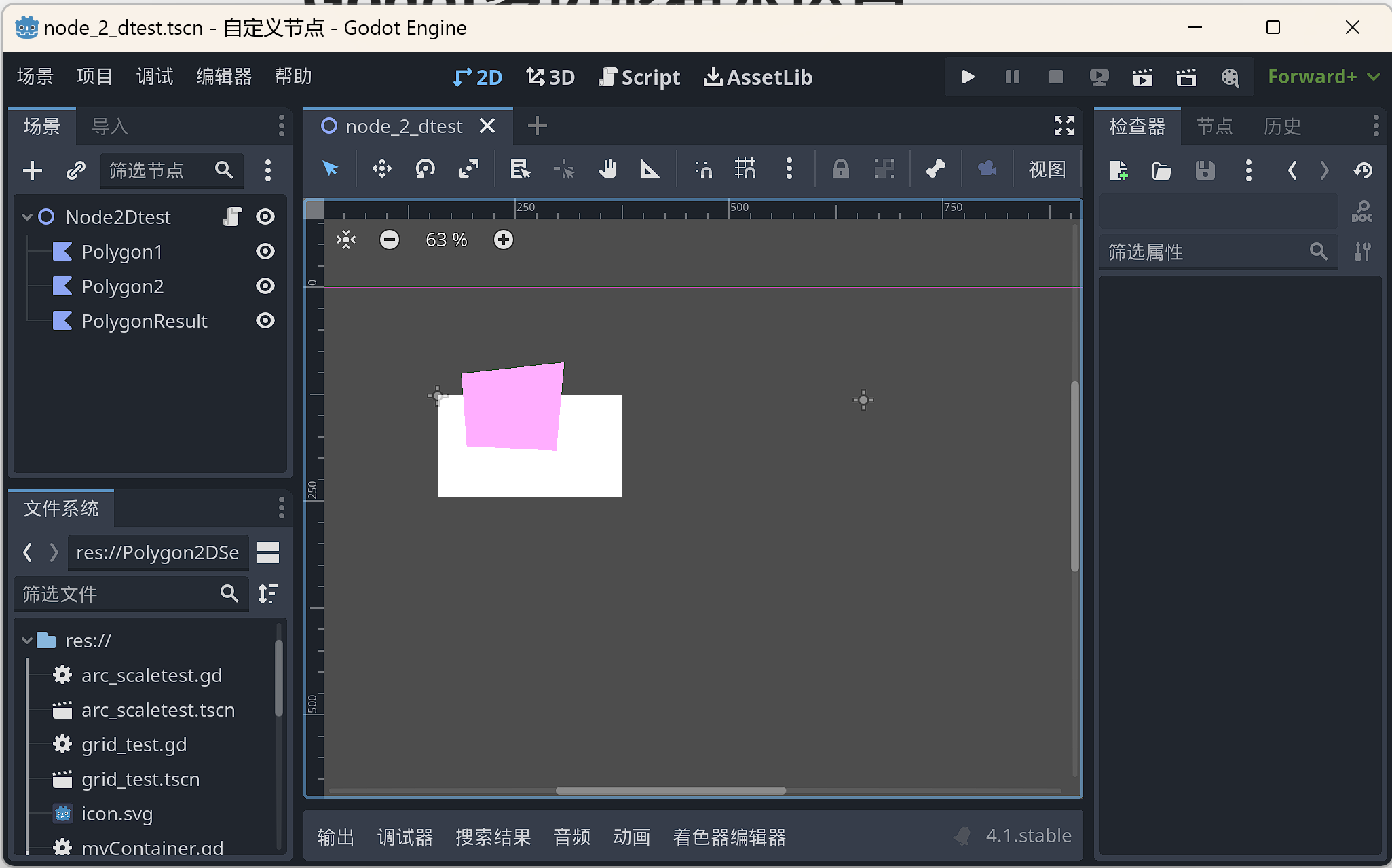
我们创建如下场景：

  • 添加3个Polygon2D节点，其中：Polygon1和Polygon2是用于布尔运算的多边形。PolygonResult用于显示布尔运算的结果。
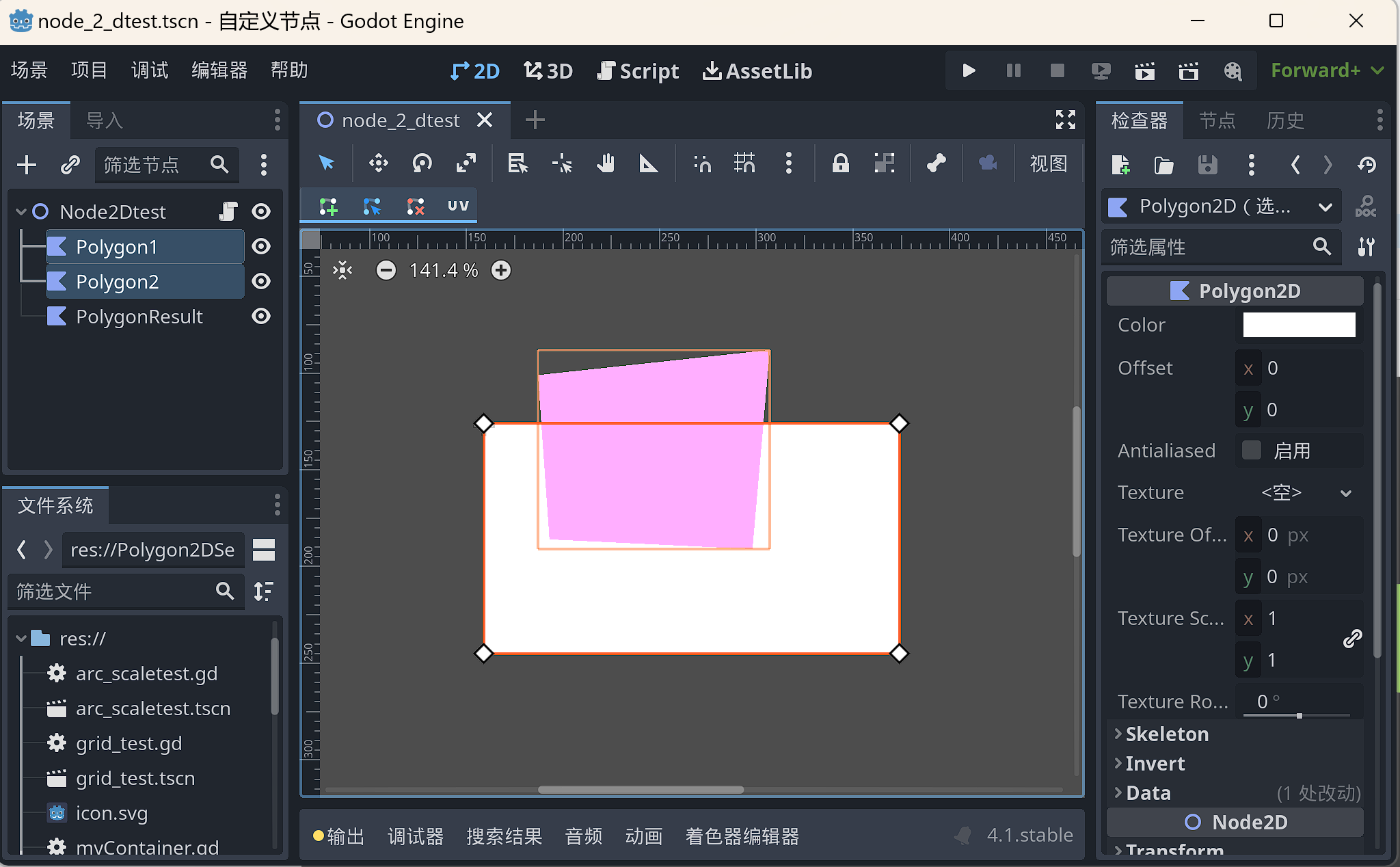
  • 我们在Polygon1和Polygon2中分别绘制一个多边形，并修改其中一个的颜色。

多边形与多边形的布尔运算测试场景

求交集

我们为根节点添加如下代码：

extends Node2D

@onready var polygon1 = $Polygon1   # 多边形1
@onready var polygon2 = $Polygon2   # 多边形2
@onready var polygon_result = $PolygonResult   # 显示布尔运算结果的Polygon2D节点


func _ready():
	var p1 = polygon1.polygon
	var p2 = polygon2.polygon
	# 显示布尔运算后的图形
	polygon_result.polygon = Geometry2D.intersect_polygons(p1,p2)[0]

运行场景后可以看到如下的结果：
进行交集运算的多边形（左），交集运算结果（右）
修改图形：
进行交集运算的多边形（左），交集运算结果（右）
再次修改：
进行交集运算的多边形（左），交集运算结果（右）

注意：Polygon1和Polygon2的原点需要对齐，否则可能会出现不准确的结果。这也很容易理解，因为原点不对齐，意味着坐标系不重合，那么整个多边形顶点的坐标就相当于发生了偏移。

Polygon1和Polygon2的原点需要对齐

亦或运算

extends Node2D

@onready var polygon1 = $Polygon1
@onready var polygon2 = $Polygon2
@onready var polygon_result = $PolygonResult
@onready var polygon_result2 = $PolygonResult2


func _ready():
	var p1 = polygon1.polygon
	var p2 = polygon2.polygon
	
	var result := Geometry2D.exclude_polygons(p1,p2)
	print(result.size())
	if result.size() == 1:
		polygon_result.polygon = result[0]
	elif result.size() == 2:
		polygon_result.polygon = result[0]
		polygon_result2.polygon = result[1]
	pass

image.png
image.png

求差集

extends Node2D

@onready var polygon1 = $Polygon1
@onready var polygon2 = $Polygon2
@onready var polygon_result = $PolygonResult
@onready var polygon_result2 = $PolygonResult2


func _ready():
	var p1 = polygon1.polygon
	var p2 = polygon2.polygon
	
	var result := Geometry2D.clip_polygons(p1,p2)
	print(result.size())
	if result.size() == 1:
		polygon_result.polygon = result[0]
	elif result.size() == 2:
		polygon_result.polygon = result[0]
		polygon_result2.polygon = result[1]
	pass

image.png
image.png
image.png

求并集

extends Node2D

@onready var polygon1 = $Polygon1
@onready var polygon2 = $Polygon2
@onready var polygon_result = $PolygonResult
@onready var polygon_result2 = $PolygonResult2


func _ready():
	var p1 = polygon1.polygon
	var p2 = polygon2.polygon
	
	var result := Geometry2D.merge_polygons(p1,p2)
	print(result.size())
	if result.size() == 1:
		polygon_result.polygon = result[0]
	elif result.size() == 2:
		polygon_result.polygon = result[0]
		polygon_result2.polygon = result[1]
	pass

image.png
image.png

总结

多边形与多边形可以进行四种布尔运算，返回的结果可能是0个，1个或多个多边形。

布尔运算方法布尔操作
交集intersect_polygonsOPERATION_INTERSECTION
并集merge_polygonsOPERATION_UNION
差集clip_polygonsOPERATION_DIFFERENCE
亦或exclude_polygonsOPERATION_XOR

PolyLine和Polygon的布尔运算

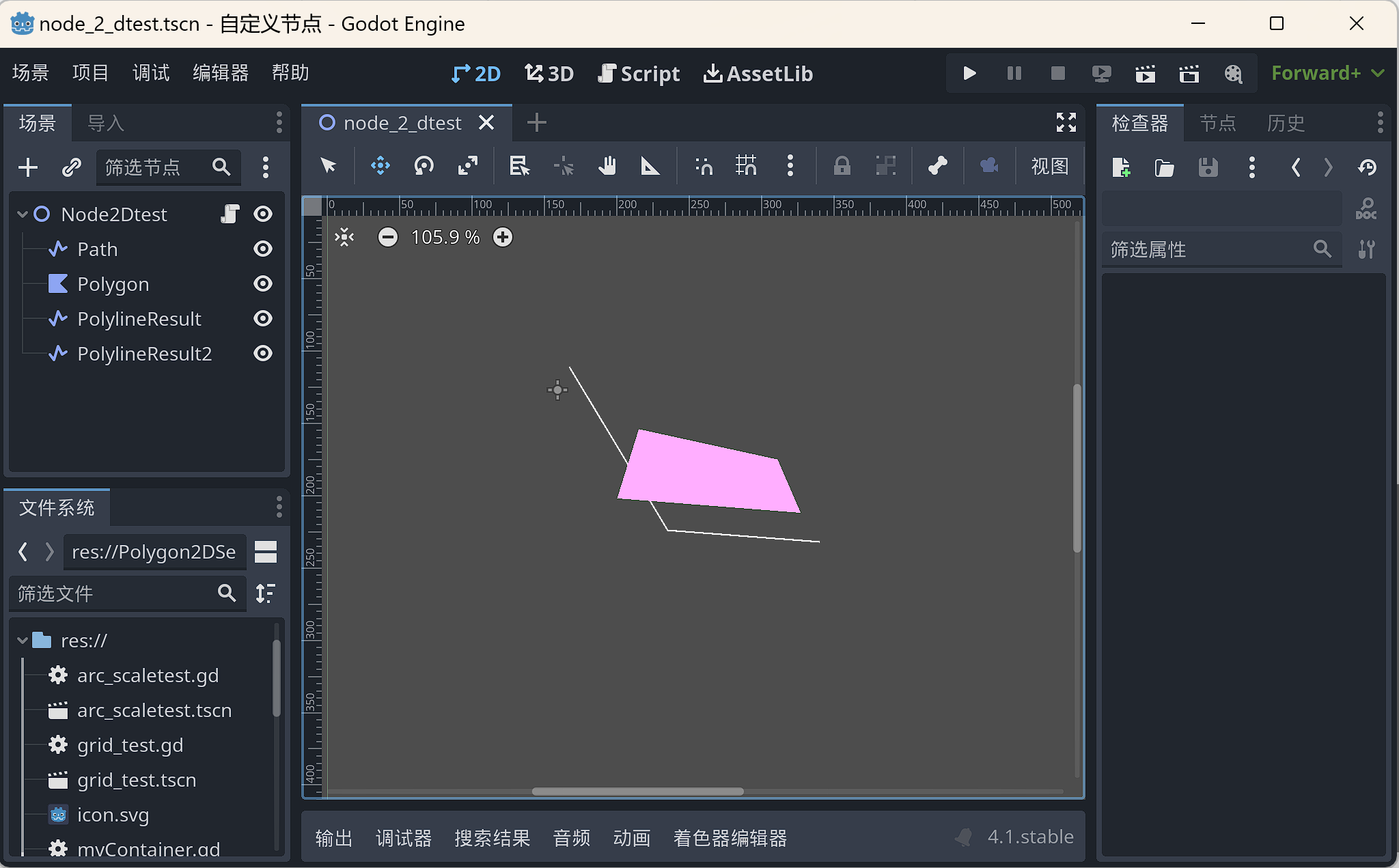
我们更改场景节点如下：
简单绘制一段折线与一个多边形。

image.png

求交集

extends Node2D

@onready var path = $Path
@onready var polygon = $Polygon
@onready var polyline_result = $PolylineResult
@onready var polyline_result2 = $PolylineResult2



func _ready():
	var l = path.points
	var p = polygon.polygon
	
	var result := Geometry2D.intersect_polyline_with_polygon(l,p)
	print(result.size())
	if result.size() == 1:
		polyline_result.points = result[0]
	pass

用多边形求与折线的交集

求差集

extends Node2D

@onready var path = $Path
@onready var polygon = $Polygon
@onready var polyline_result = $PolylineResult
@onready var polyline_result2 = $PolylineResult2



func _ready():
	var l = path.points
	var p = polygon.polygon
	
	var result := Geometry2D.clip_polyline_with_polygon(l,p)
	print(result)
	if result.size() == 1:
		polyline_result.points = result[0]
	elif result.size() == 2:
		polyline_result.points = result[0]
		polyline_result2.points = result[1]
	pass

用多边形求与折线的差集
image.png

总结

多边形与折线只能求交集或差集，返回的可能是一条或多条折线。

布尔运算方法布尔操作
交集intersect_polyline_with_polygonOPERATION_INTERSECTION
差集clip_polyline_with_polygonOPERATION_DIFFERENCE

求交点

判断两条直线是否相交以及获得交点

@tool
extends Control

var line1 = [Vector2(0,0),Vector2(400,400)]
var line2 = [Vector2(350,150),Vector2(10,300)]

func _draw():
	draw_line(line1[0],line1[1],Color.GOLDENROD,2)
	draw_line(line2[0],line2[1],Color.GREEN_YELLOW,2)
	if Geometry2D.line_intersects_line(line1[0],line1[0].direction_to(line1[1]),line2[0],line2[0].direction_to(line2[1])):
		var j_point:Vector2 = Geometry2D.line_intersects_line(line1[0],line1[0].direction_to(line1[1]),line2[0],line2[0].direction_to(line2[1]))
		draw_circle(j_point,4,Color.BLUE_VIOLET)

判断并求取两条直线的交点

判断线段与圆是否相交以及获得焦点

extends Node2D

# 定义圆
var center = Vector2(400,200)
var r = 50

var pos:Vector2

func _process(delta):
	pos = get_global_mouse_position()
	queue_redraw()

func _draw():
	# 绘制圆
	draw_circle(center,r,Color.AQUA)
	# 绘制线段
	var line = [center,pos]
	draw_line(line[0],line[1],Color.YELLOW)
	var x = Geometry2D.segment_intersects_circle(line[0],line[1],center,r) # 判断与圆是否有交点
	if x:
		var x_pos = lerp(line[0],line[1],x)
		draw_circle(x_pos,5,Color.ORANGE_RED)
  • segment_intersects_circle判断一个线段与圆的边界是否有交点
  • 如果没有交点，则返回-1,如果有则返回一个0.0-1.0之间的数字
  • 这个数字返回的是焦点在线段上的偏移值（从起始点到终点）
  • 通过lerp(线段起始点,线段终点,偏移值)形式，我们就可以获得实际交点的位置

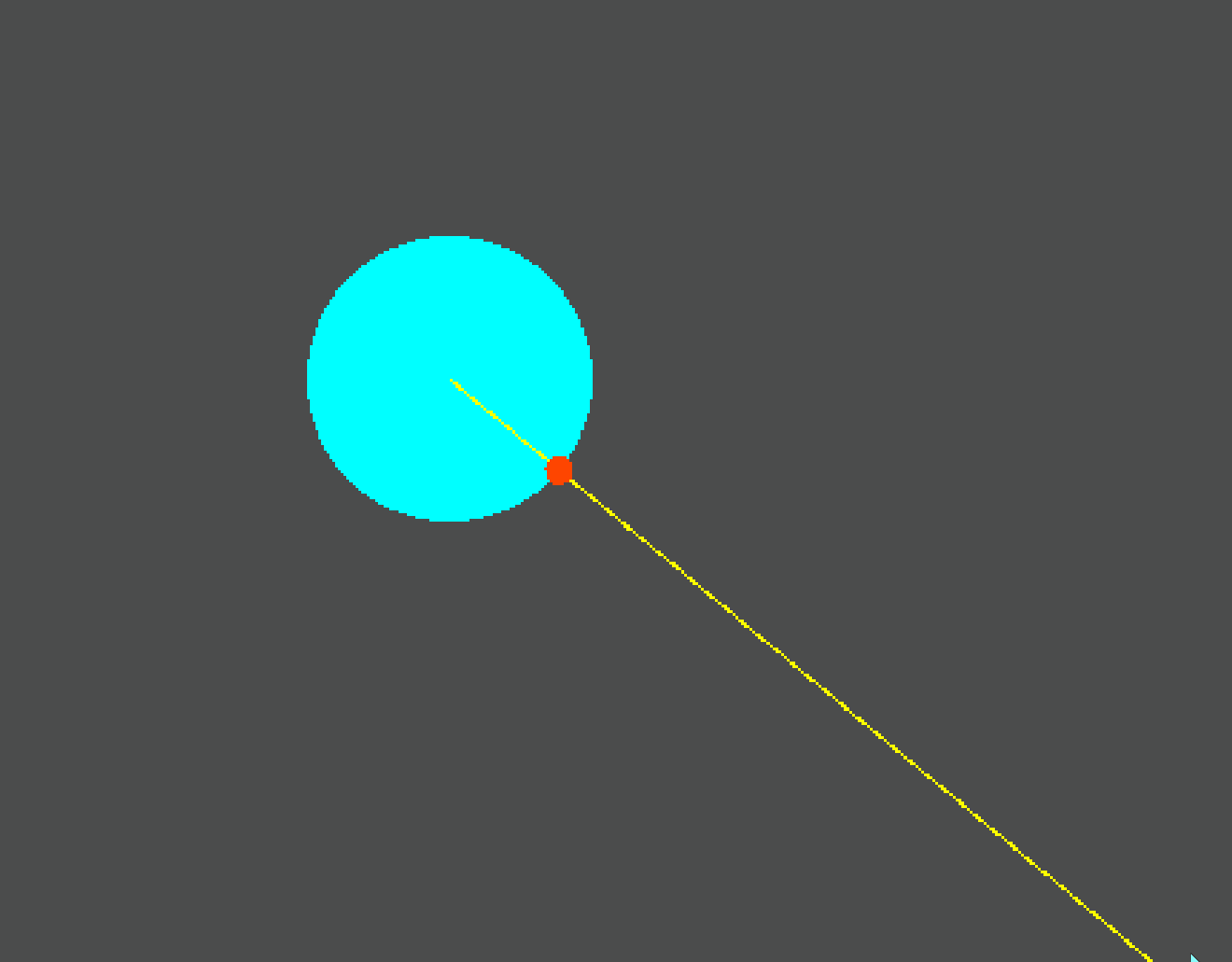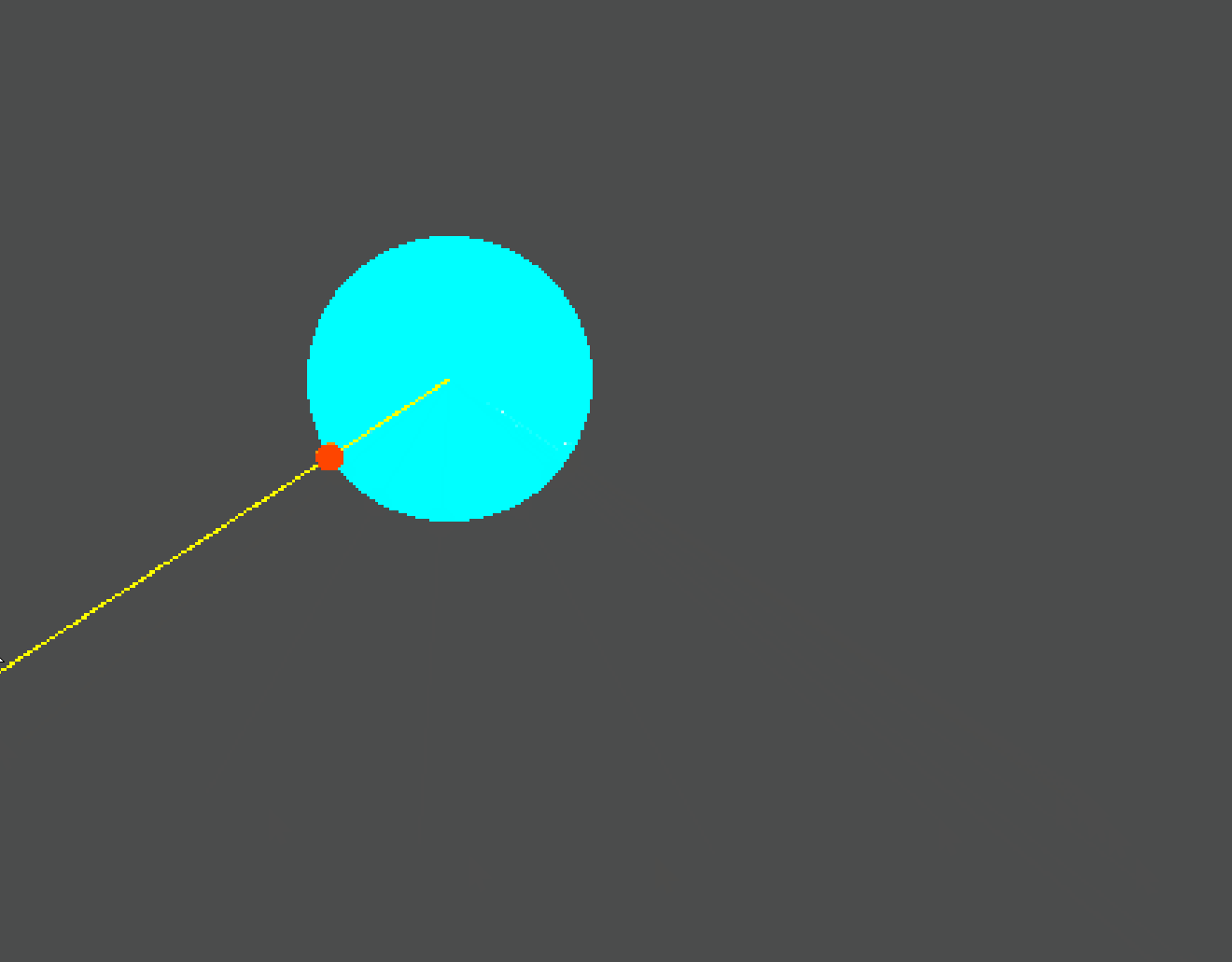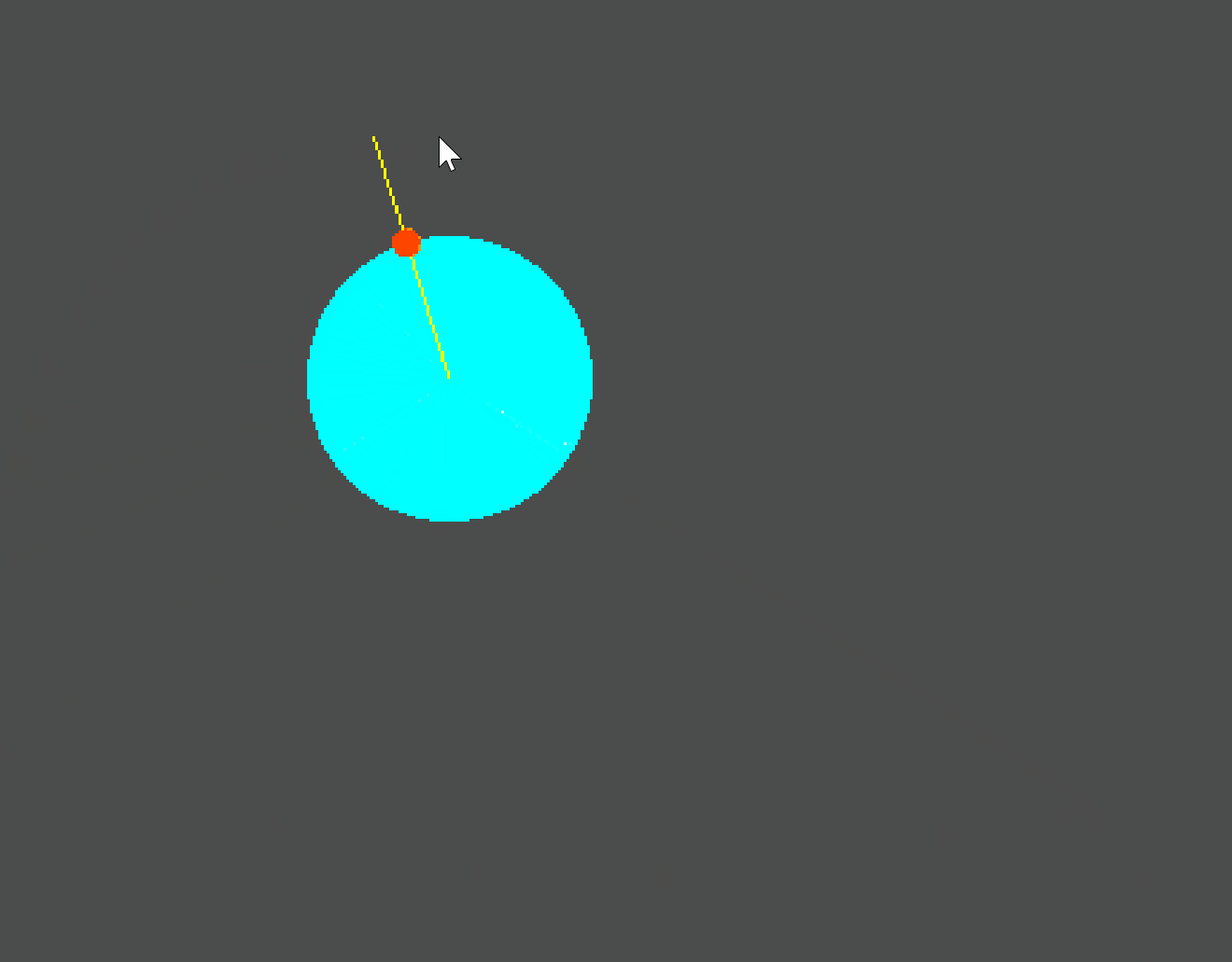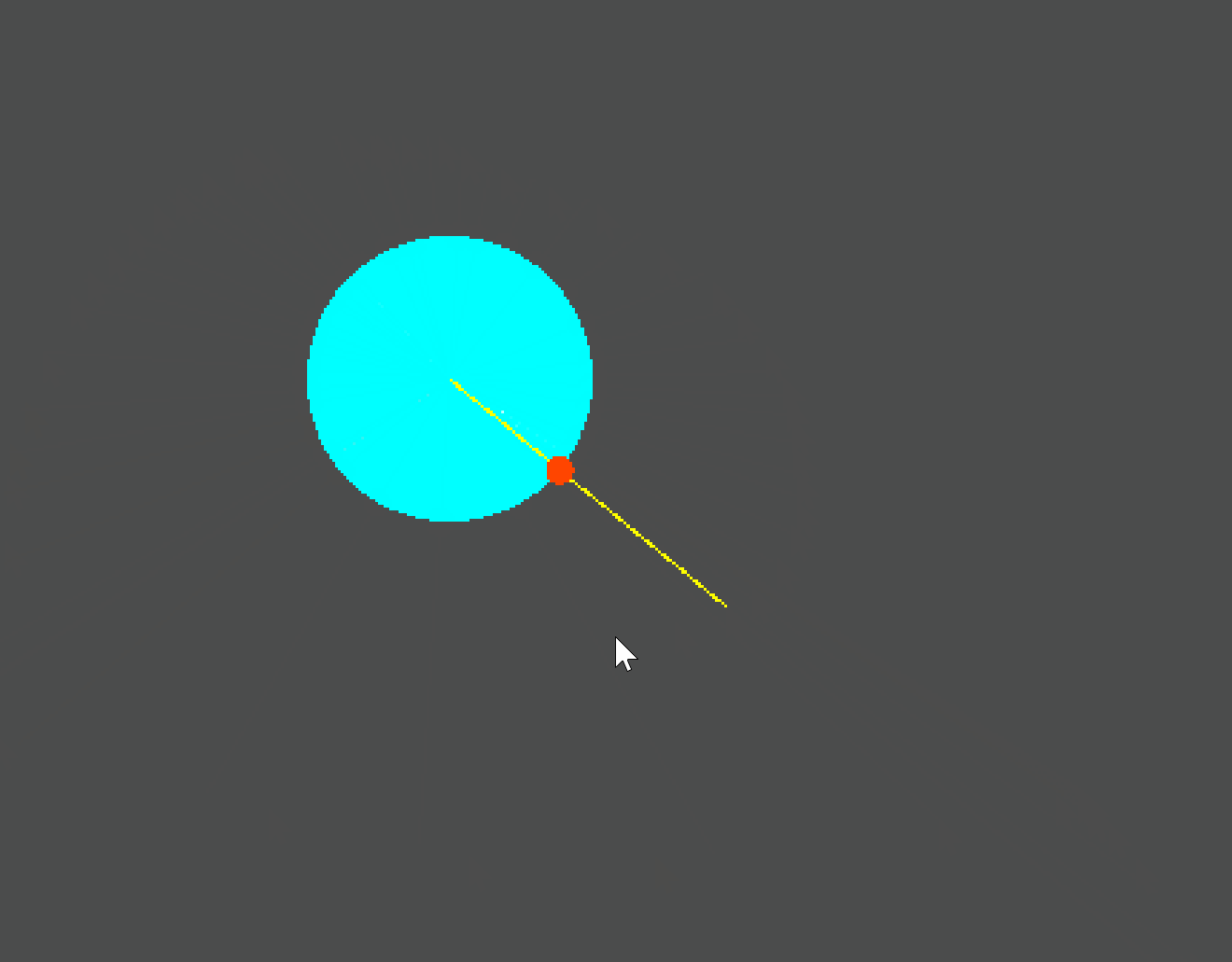
请添加图片描述
请添加图片描述
请添加图片描述
通过观察线段起点不是圆心的情况，可以发现求得的交点是类似于RayCast2D求得的碰撞点，也就是首先接触的那个交点。

其实通过求反向线段与圆的交点，就可以同时求出两个交点。

# 求反向线段 （颠倒起始点、终点）
var line2 = line.duplicate()
line2.reverse()

效果：
请添加图片描述

完整代码：

extends Node2D

# 定义圆
var center = Vector2(400,200)
var r = 50

var pos:Vector2

func _process(delta):
	pos = get_global_mouse_position()
	queue_redraw()

func _draw():
	# 绘制圆
	draw_circle(center,r,Color.AQUA)
	# 绘制线段
	var line = [center+Vector2(200,200),pos]
	var line2 = line.duplicate()
	line2.reverse()
	draw_line(line[0],line[1],Color.YELLOW)
	var x = Geometry2D.segment_intersects_circle(line[0],line[1],center,r) # 判断与圆是否有交点
	if x != -1:
		var x_pos = lerp(line[0],line[1],x)
		draw_circle(x_pos,5,Color.ORANGE_RED)
	var x2 = Geometry2D.segment_intersects_circle(line2[0],line2[1],center,r) # 判断与圆是否有交点
	if x2 != -1:
		var x2_pos = lerp(line2[0],line2[1],x2)
		draw_circle(x2_pos,5,Color.ORANGE_RED)

判断点是否在一个几何图形内

如果你熟悉Rect2的话，你就会知道它有一个名叫has_point的方法，可以判断一个点是否在矩形内。最常见的用途就是判断鼠标是否进入矩形区域内或移出。

Geometry2D则提供了对圆形、多边形和三角形判断一个点是否在其内部的方法。

判断点是否在圆内

@tool
extends Control

var pos:Vector2

func _process(delta):
	pos = get_global_mouse_position()
	queue_redraw()

func _draw():
	var center = Vector2(400,200)
	var r = 50
	if Geometry2D.is_point_in_circle(pos,center,r): # 鼠标进入圆
		draw_circle(center,r,Color.AQUA)
	else: # 鼠标在圆外
		draw_circle(center,r,Color.AQUAMARINE)
	
	draw_circle(pos,4,Color.ORANGE) # 绘制鼠标位置

判断鼠标是否进入圆的区域

判断点是否在多边形内

@tool
extends Control

var polygon:PackedVector2Array = [
	Vector2(100,100),Vector2(300,100),
	Vector2(450,150),Vector2(300,300),
	Vector2(200,200),Vector2(100,100)
]
var pos:Vector2

func _process(delta):
	pos = get_global_mouse_position()
	queue_redraw()

func _draw():
	if Geometry2D.is_point_in_polygon(pos,polygon): # 鼠标进入圆
		draw_polygon(polygon,[Color.AQUA])
	else: # 鼠标在圆外
		draw_polygon(polygon,[Color.AQUAMARINE])
	
	draw_circle(pos,4,Color.ORANGE) # 绘制鼠标位置

判断鼠标是否进入多边形区域

判断点是否在三角形内

@tool
extends Control

var polygon:PackedVector2Array = [
	Vector2(100,100),Vector2(300,100),
	Vector2(250,350)
]
var pos:Vector2

func _process(delta):
	pos = get_global_mouse_position()
	queue_redraw()

func _draw():
	if Geometry2D.point_is_inside_triangle(pos,polygon[0],polygon[1],polygon[2]): # 鼠标进入三角形
		draw_polygon(polygon,[Color.AQUA])
	else: # 鼠标在三角形外
		draw_polygon(polygon,[Color.AQUAMARINE])
	
	draw_circle(pos,4,Color.ORANGE) # 绘制鼠标位置

判断鼠标点是否在三角形内

获取最近点

求取线段上离鼠标位置最近的点

@tool
extends Control

var line1 = [Vector2(0,0),Vector2(400,400)]
var pos:Vector2

func _process(delta):
	pos = get_global_mouse_position()
	queue_redraw()

func _draw():
	draw_line(line1[0],line1[1],Color.GOLDENROD,2)
	var c_point = Geometry2D.get_closest_point_to_segment(pos,line1[0],line1[1])
	draw_circle(c_point,4,Color.GREEN_YELLOW)
	draw_circle(pos,4,Color.BLUE)

求取线段上离鼠标位置最近的点
可以看到：

  • 如果鼠标点在与线段平行的所有线段组成的无限矩形范围内，则最近点就是垂线与线段的交点。
  • 如果超出线段端点范围，则最近点停留在端点上。

求取直线上离鼠标最近的点

@tool
extends Control

var line1 = [Vector2(0,0),Vector2(400,400)]
var pos:Vector2

func _process(delta):
	pos = get_global_mouse_position()
	queue_redraw()

func _draw():
	draw_line(line1[0],line1[1],Color.GOLDENROD,2)
	var c_point = Geometry2D.get_closest_point_to_segment_uncapped(pos,line1[0],line1[1])
	draw_circle(c_point,4,Color.GREEN_YELLOW)
	draw_circle(pos,4,Color.BLUE)

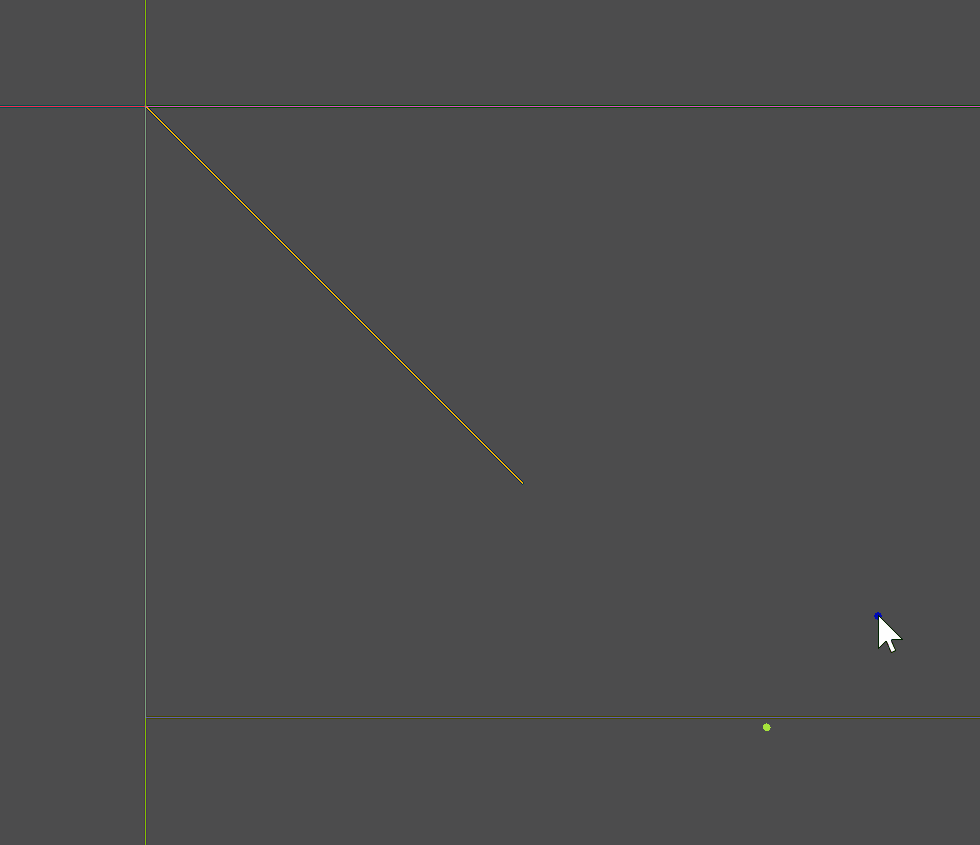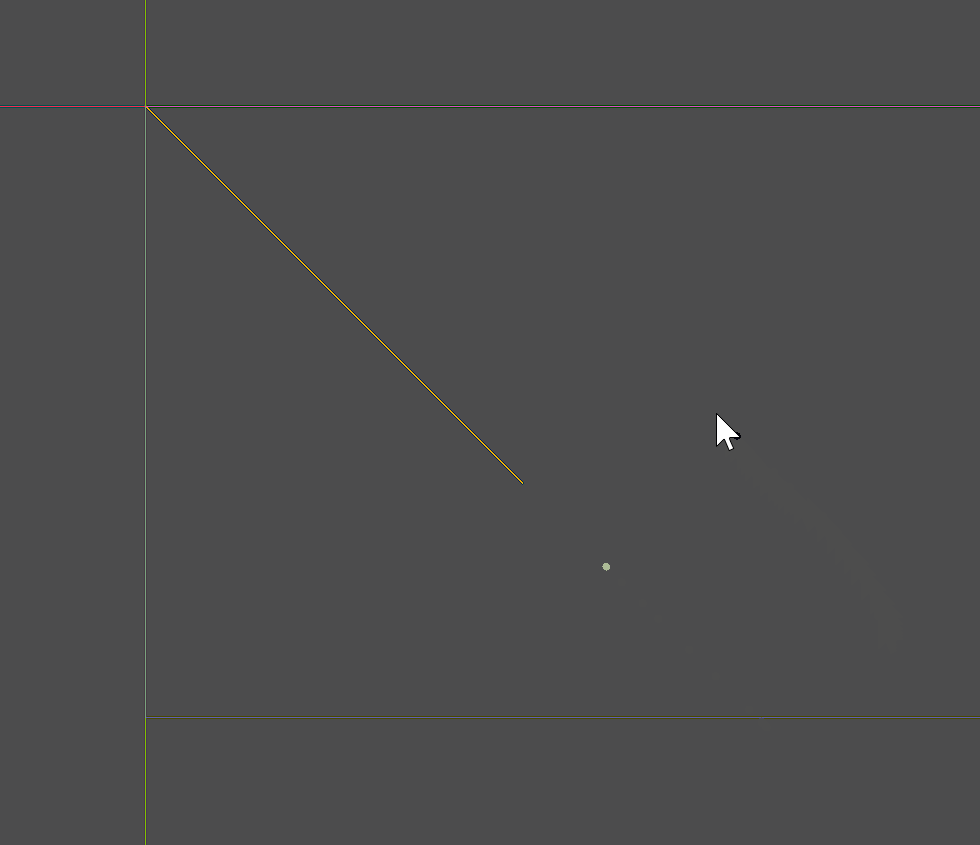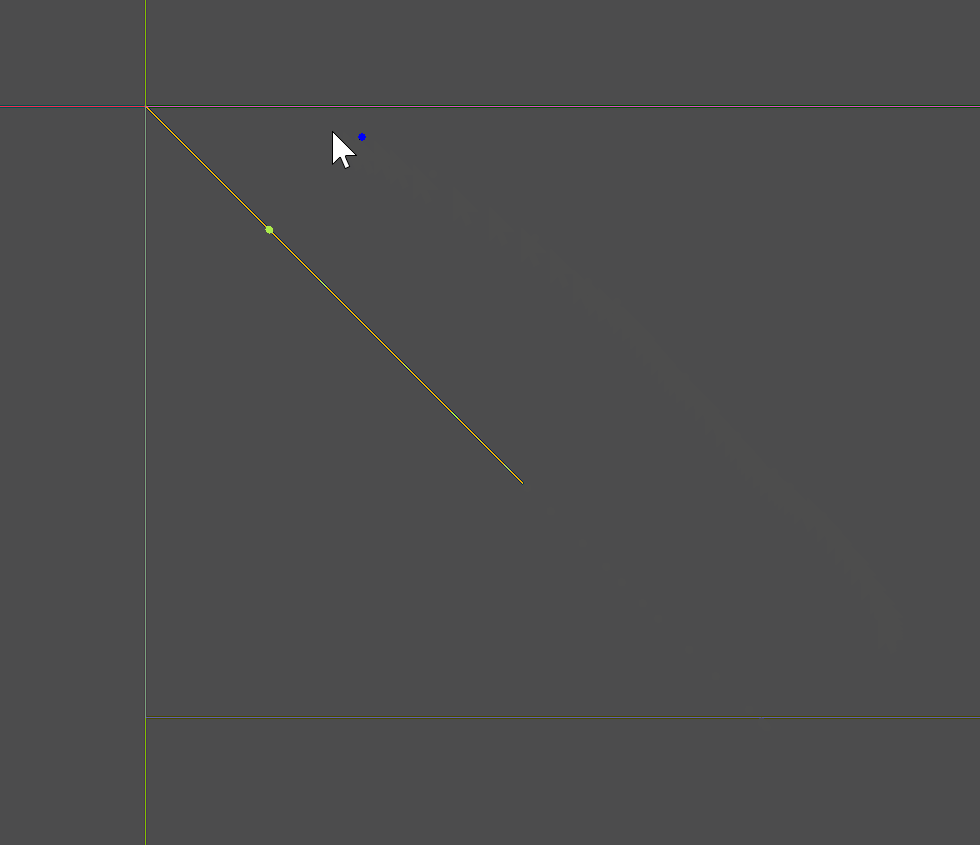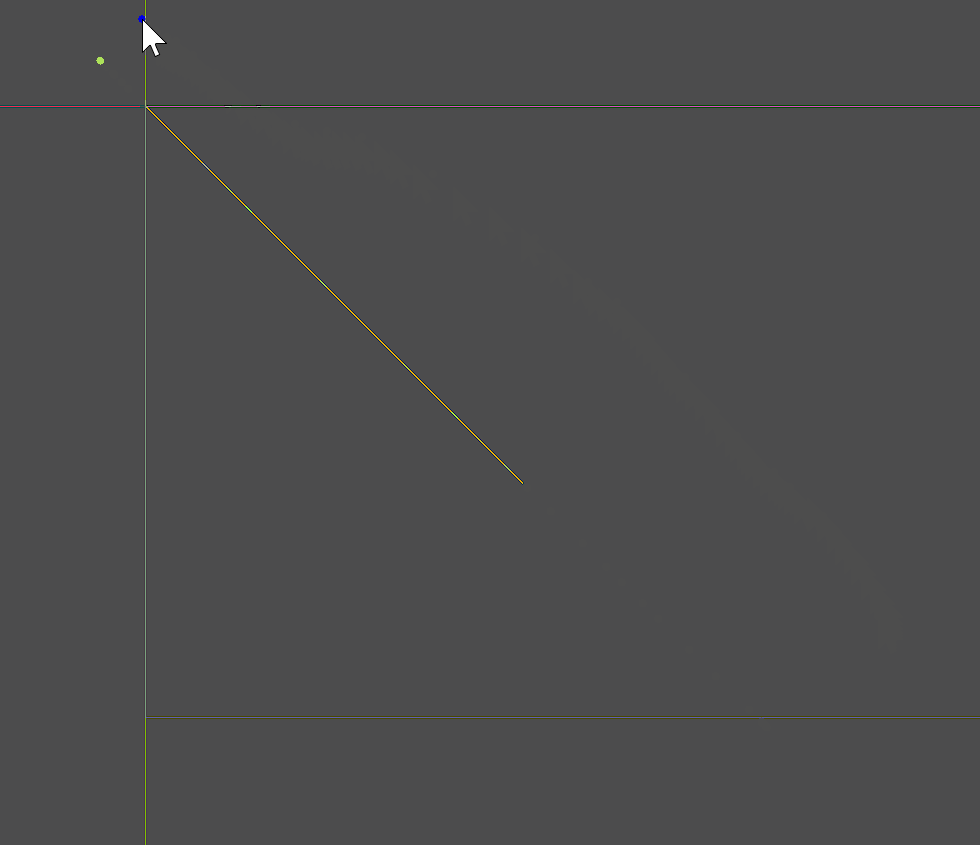
求取直线上离鼠标最近的点
与线段的概念不同，直线是一个无限长的几何图形，所以求某个点离直线最近的点，就是经过该点做直线的垂线时，获得的交点。

求取两条线段之间最近的两个点

@tool
extends Control

var line1 = [Vector2(100,100),Vector2(400,100)]
var line2 = [Vector2(200,200),Vector2(500,500)]
var pos:Vector2

func _process(delta):
	line2[1] = get_global_mouse_position()
	queue_redraw()

func _draw():
	draw_line(line1[0],line1[1],Color.GOLDENROD,2)
	draw_line(line2[0],line2[1],Color.ORANGE_RED,2)
	var c_points:PackedVector2Array = Geometry2D.get_closest_points_between_segments(line1[0],line1[1],line2[0],line2[1])
	draw_circle(c_points[0],4,Color.GREEN_YELLOW)
	draw_circle(c_points[1],4,Color.GREEN_YELLOW)

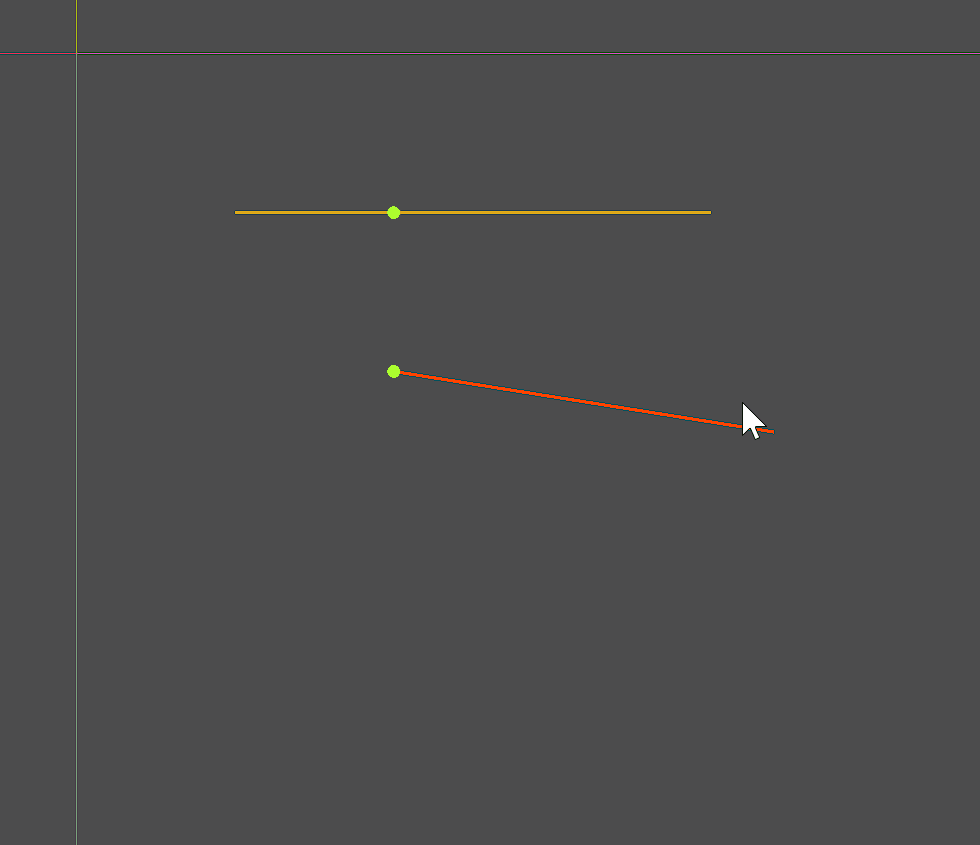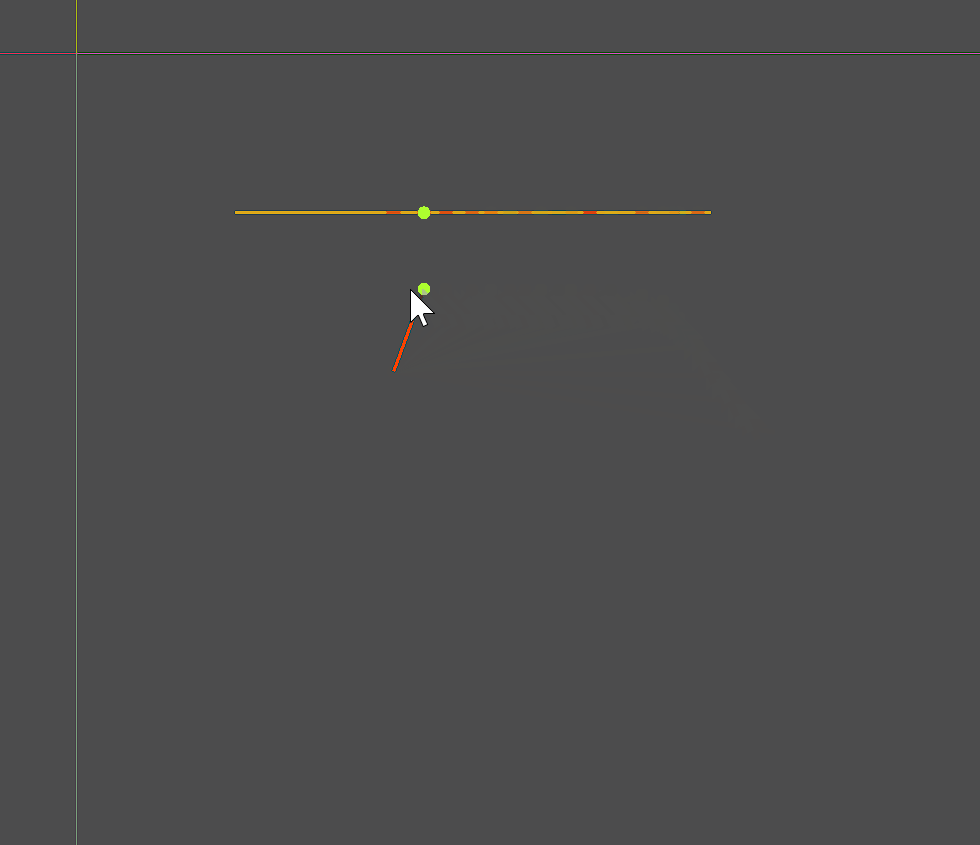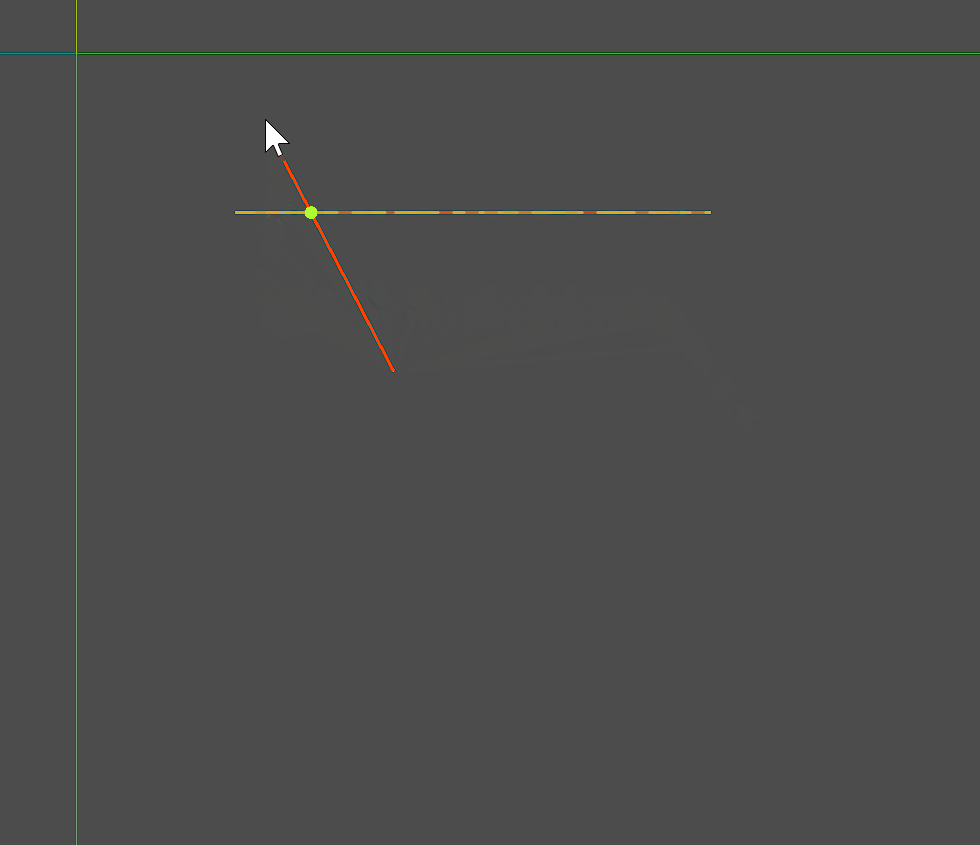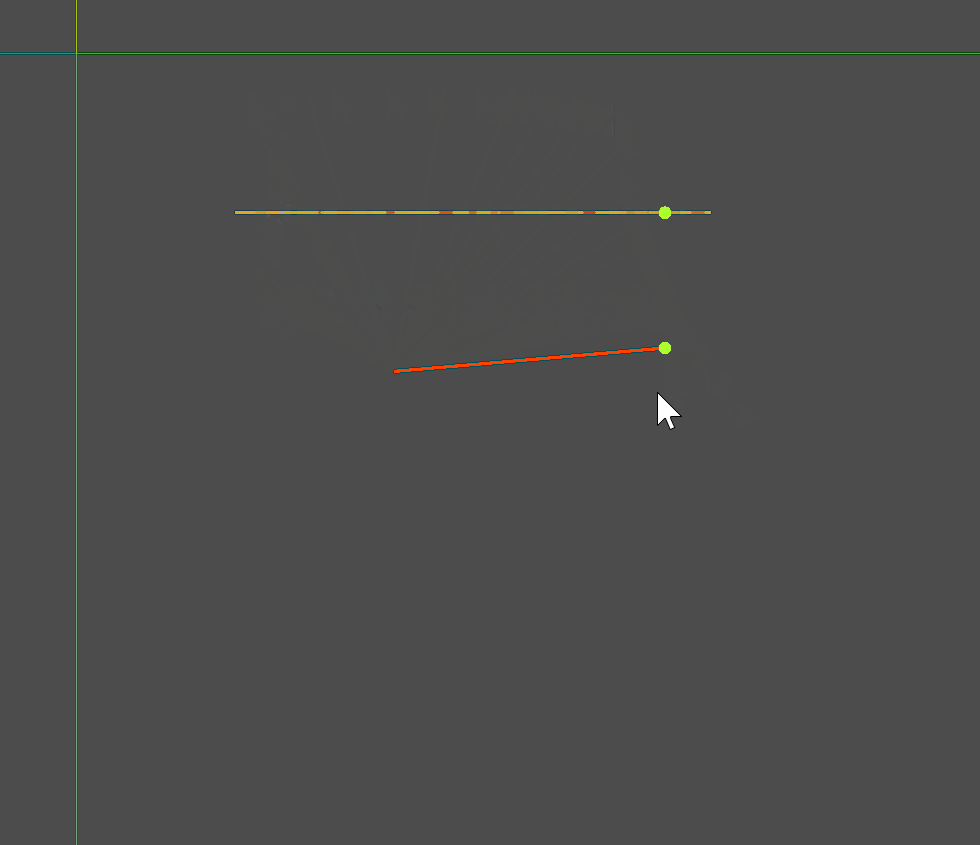
求取两条线段之间最近的两个点

两条线段，固定其中一条：

  • 如果不相交，则最近点就是求经过动态线段两个端点中离固定线段比较近的一个端点做垂线的交点（。。。我自己也觉得绕）
  • 如果相交，就是交点。

膨胀或缩小多边形

圆角化膨胀或缩小

@tool
extends Control

@export var offset:int = 0:
	set(val):
		offset = val
		queue_redraw()


var polygon:PackedVector2Array = ShapePoints.star(0,5,50,30,Vector2(400,200))
var pos:Vector2

func _draw():
	var off_polygon = Geometry2D.offset_polygon(polygon,offset,Geometry2D.JOIN_ROUND)[0]
	draw_polygon(off_polygon,[Color.AQUAMARINE])

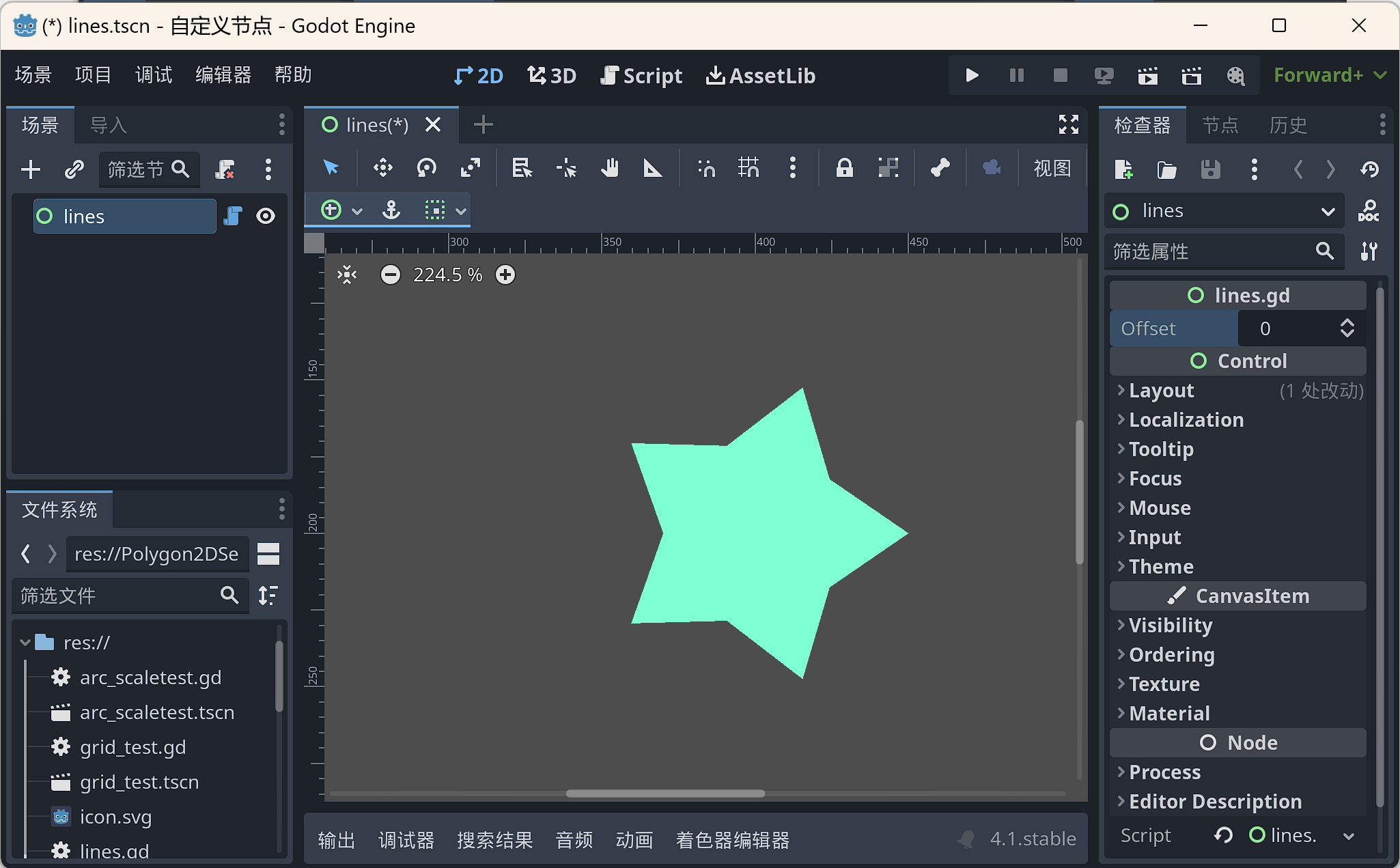
最初的五角星
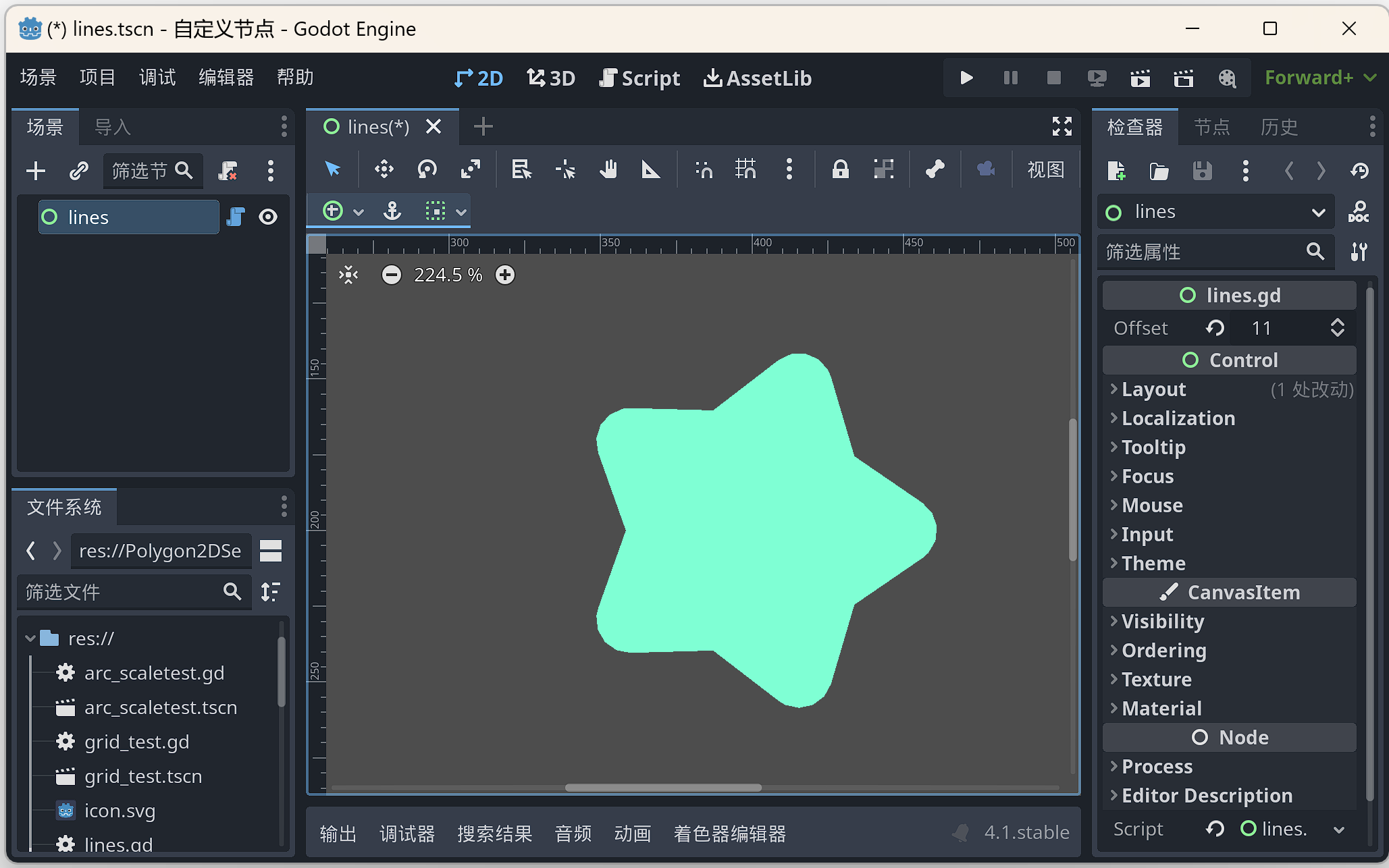
通过圆角化膨胀后的五角星

保持尖角的膨胀和缩小

@tool
extends Control

@export var offset:int = 0:
	set(val):
		offset = val
		queue_redraw()


var polygon:PackedVector2Array = ShapePoints.star(0,5,50,30,Vector2(400,200))
var pos:Vector2

func _draw():
	var off_polygon = Geometry2D.offset_polygon(polygon,offset,Geometry2D.JOIN_MITER)[0]
	draw_polygon(off_polygon,[Color.AQUAMARINE])

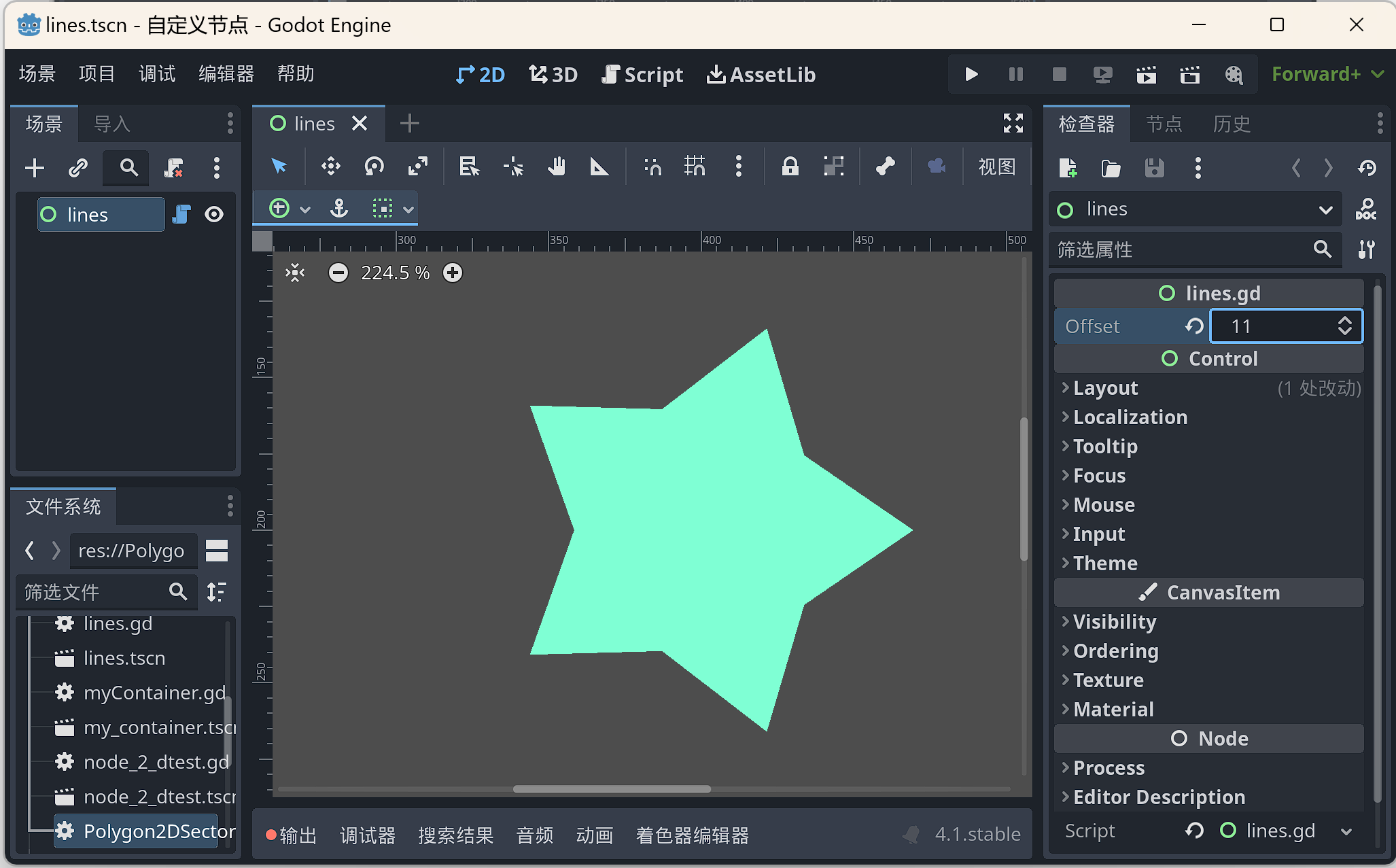
保持尖角膨胀后的五角星

切角化的膨胀或缩小

@tool
extends Control

@export var offset:int = 0:
	set(val):
		offset = val
		queue_redraw()


var polygon:PackedVector2Array = ShapePoints.star(0,5,50,30,Vector2(400,200))
var pos:Vector2

func _draw():
	var off_polygon = Geometry2D.offset_polygon(polygon,offset,Geometry2D.JOIN_SQUARE)[0]
	draw_polygon(off_polygon,[Color.AQUAMARINE])

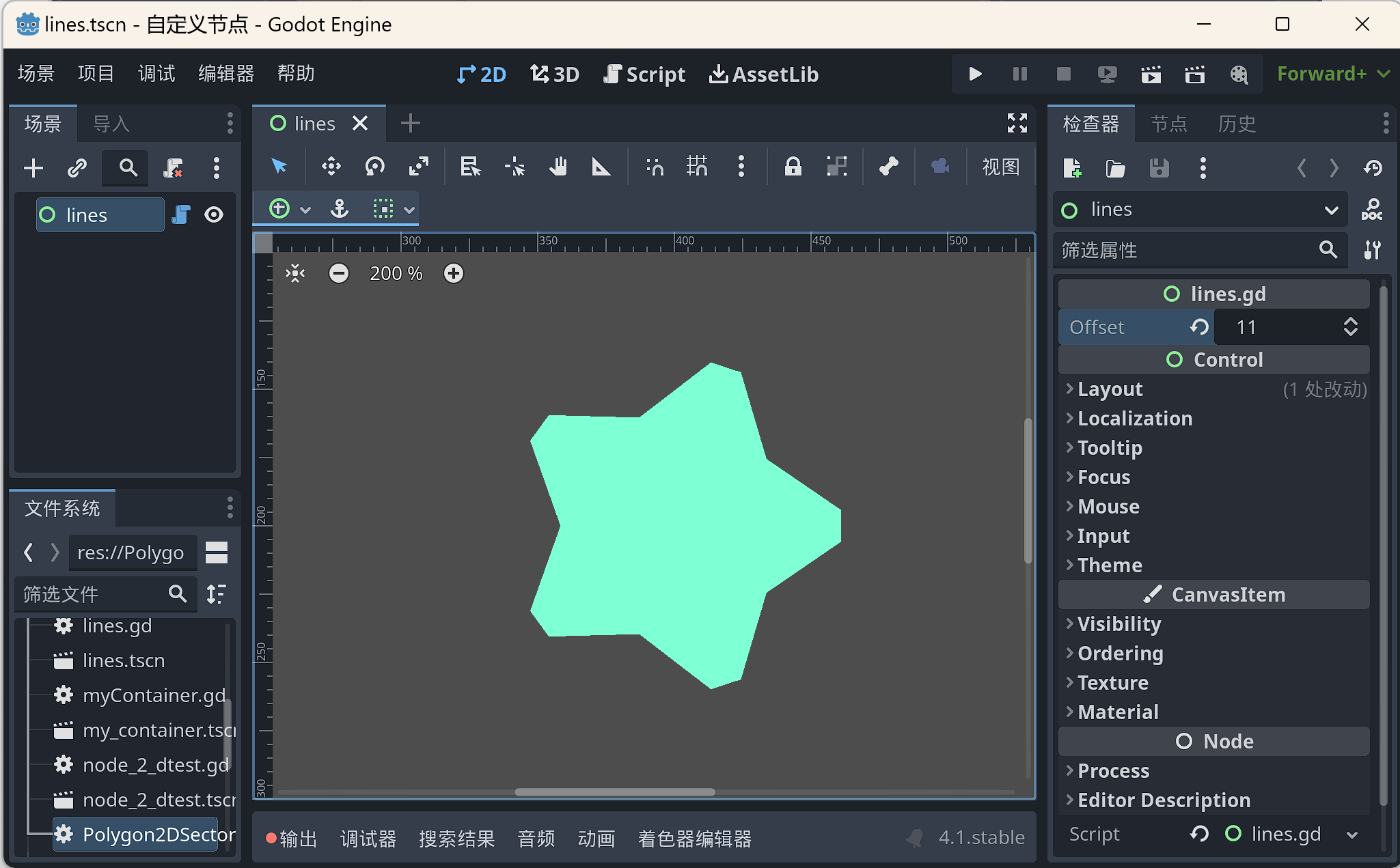
切角化膨胀后的五角星
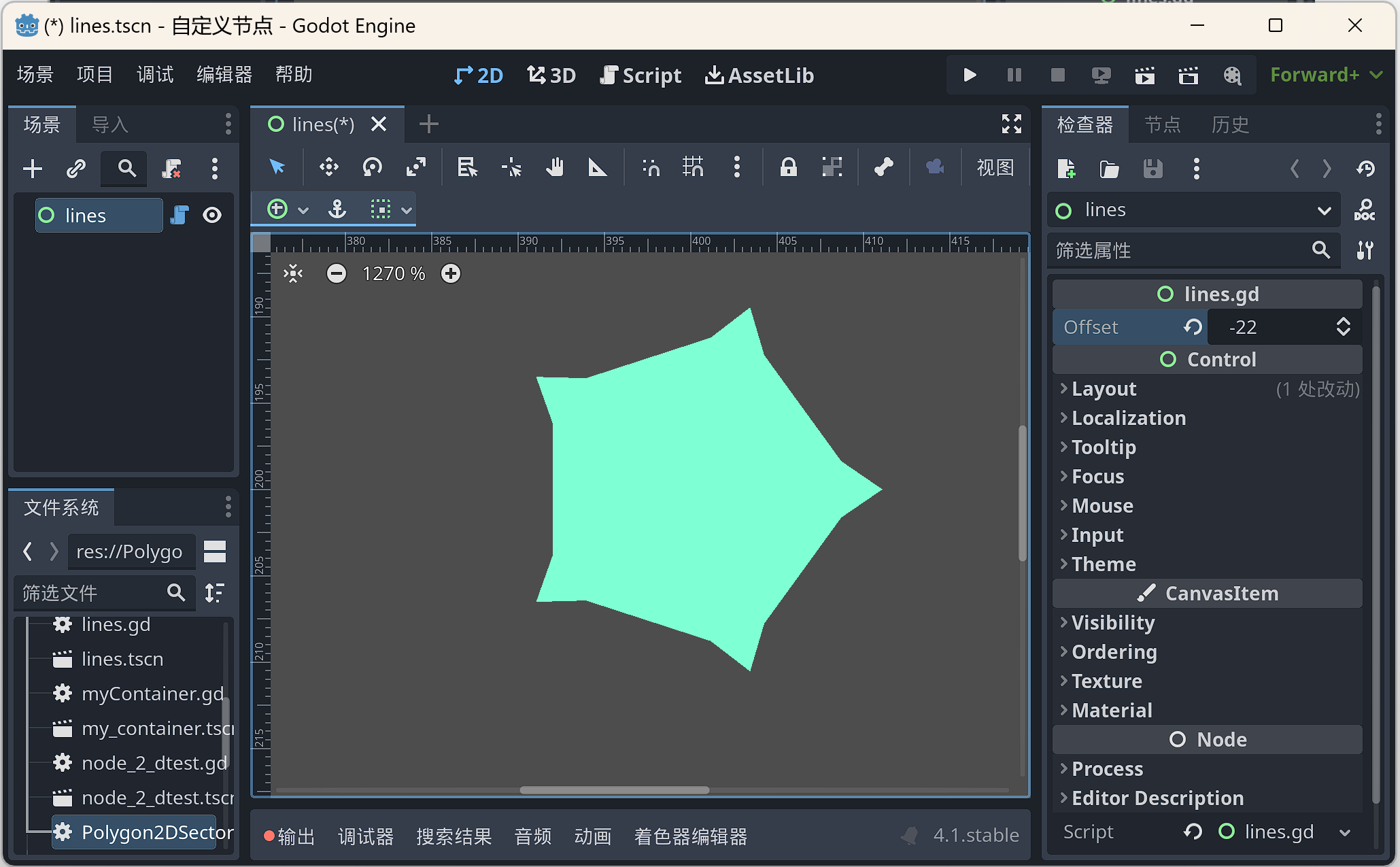
切角化收缩后的五角星

分解凹多边形为几个凸多边形

var result := Geometry2D.decompose_polygon_in_convex(p1)

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
可以看到，如果一个多边形是凹多边形（Concave Polygon），那么使用decompose_polygon_in_convex方法，会将其拆分为若干个凸多边形。

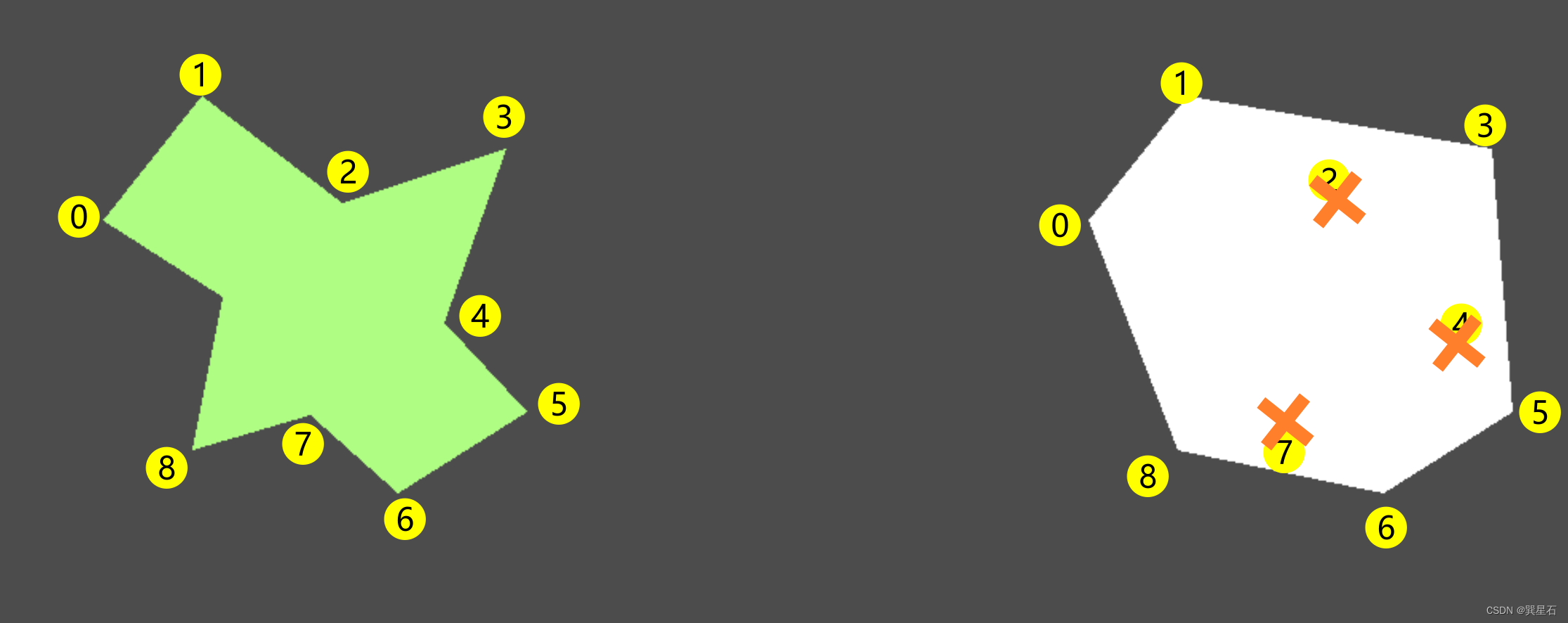
从凹多边形求凸多边形

var result := Geometry2D.convex_hull(p1)
print(p1)
print(result)

在这里插入图片描述

[(195, 152), (257, 74), (345, 141), (448, 107), (409, 216), (461, 272), (380, 323), (325, 274), (251, 296), (270, 200)]
[(195, 152), (257, 74), (448, 107), (461, 272), (380, 323), (251, 296), (195, 152)]

可以看到，其结果是删除了所有凹进去的点，最后形成一个完全包裹原来凹多边形的凸多边形。
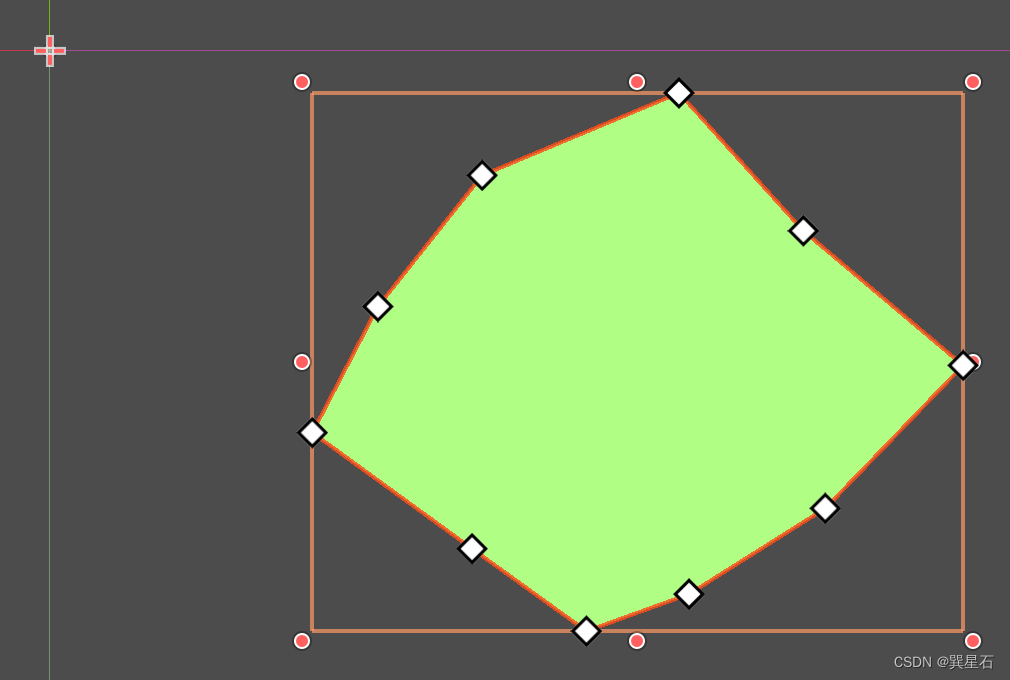
在这里插入图片描述
其他的一些尝试：

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

获取多边形的矩形尺寸

对于下图所示的多边形，我们使用make_atlas：

var p1 = polygon1.polygon
print(JSON.stringify(Geometry2D.make_atlas(p1),"\t"))

在这里插入图片描述

打印内容：

{
	"points": "[(251, 940), (693, 595), (0, 294), (0, 187), (0, 0), (543, 0), (448, 272), (374, 595), (0, 319), (446, 940)]",
	"size": "(1004, 1167)"
}

可以看到结果是一个字典，包含两个键：

  • points返回的是图形顶点数据
  • size返回一个尺寸，但是我暂时没有搞懂它的含义，它的尺寸是一个远大于多边形包围盒尺寸的

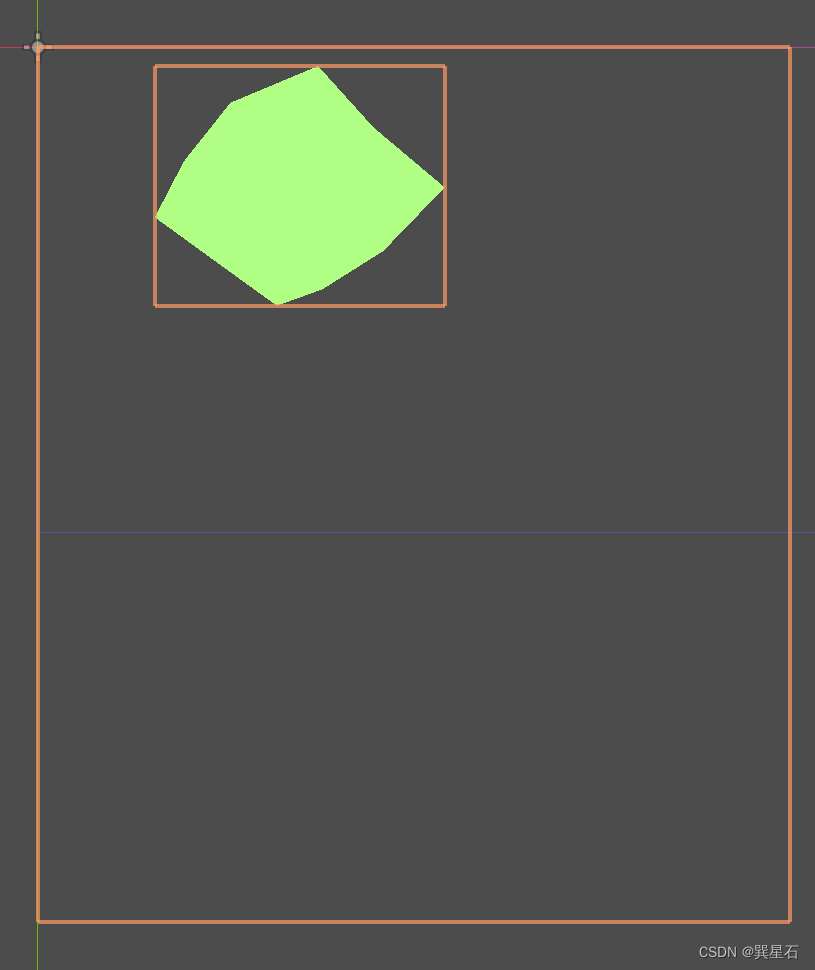
在这里插入图片描述

任意多边形包围盒position、end和size求取函数

  • 通过求所有顶点中最小的x和y组成的Vector2就可以得到多边形包围盒Rect2的左上角顶点position。
  • 通过求所有顶点中最大的x和y组成的Vector2就可以得到多边形包围盒Rect2的右下角顶点end。
  • Rect2的尺寸size = end - position
  • Rect2的中心点center = position + size/2.0
# 求任意多边形包围盒Rect2的position
func get_polygon_Rect2_position(polygon:PackedVector2Array) -> Vector2:
	var xs = []  # 所有的x
	var ys = []  # 所有的y
	for i in range(polygon.size()):
		xs.append(polygon[i].x)
		ys.append(polygon[i].y)
	# 升序排列
	xs.sort()
	ys.sort() 
	return Vector2(xs[0],ys[0]) # 返回由最小的x和y组成的点坐标
	
# 求任意多边形包围盒Rect2的end
func get_polygon_Rect2_end(polygon:PackedVector2Array) -> Vector2:
	var xs = []  # 所有的x
	var ys = []  # 所有的y
	for i in range(polygon.size()):
		xs.append(polygon[i].x)
		ys.append(polygon[i].y)
	# 降序排列
	xs.sort()
	xs.reverse()
	ys.sort()
	ys.reverse()
	return Vector2(xs[0],ys[0]) # 返回由最大的x和y组成的点坐标

# 求任意多边形包围盒Rect2的size
func get_polygon_Rect2_size(polygon:PackedVector2Array) -> Vector2:
	var size:Vector2
	var position = get_polygon_Rect2_position(polygon)
	var end = get_polygon_Rect2_end(polygon)
	if end > position:
		size = end - position
	else:
		size =  position - end
	return size

# 求任意多边形包围盒Rect2的center
func get_polygon_Rect2_center(polygon:PackedVector2Array) -> Vector2:
	var size = get_polygon_Rect2_size(polygon)
	var position = get_polygon_Rect2_position(polygon)
	return position + size/2.0

通过设定一个空的控件尺寸，可以验证结果的正确性：
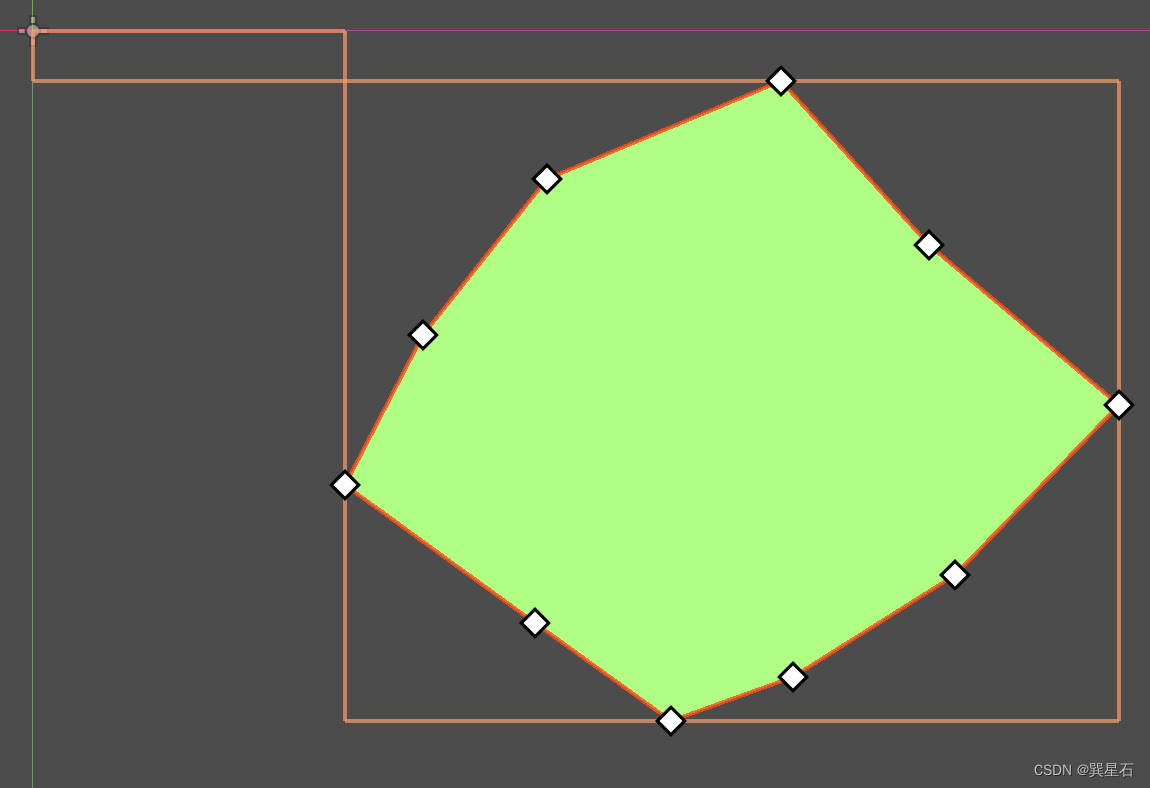
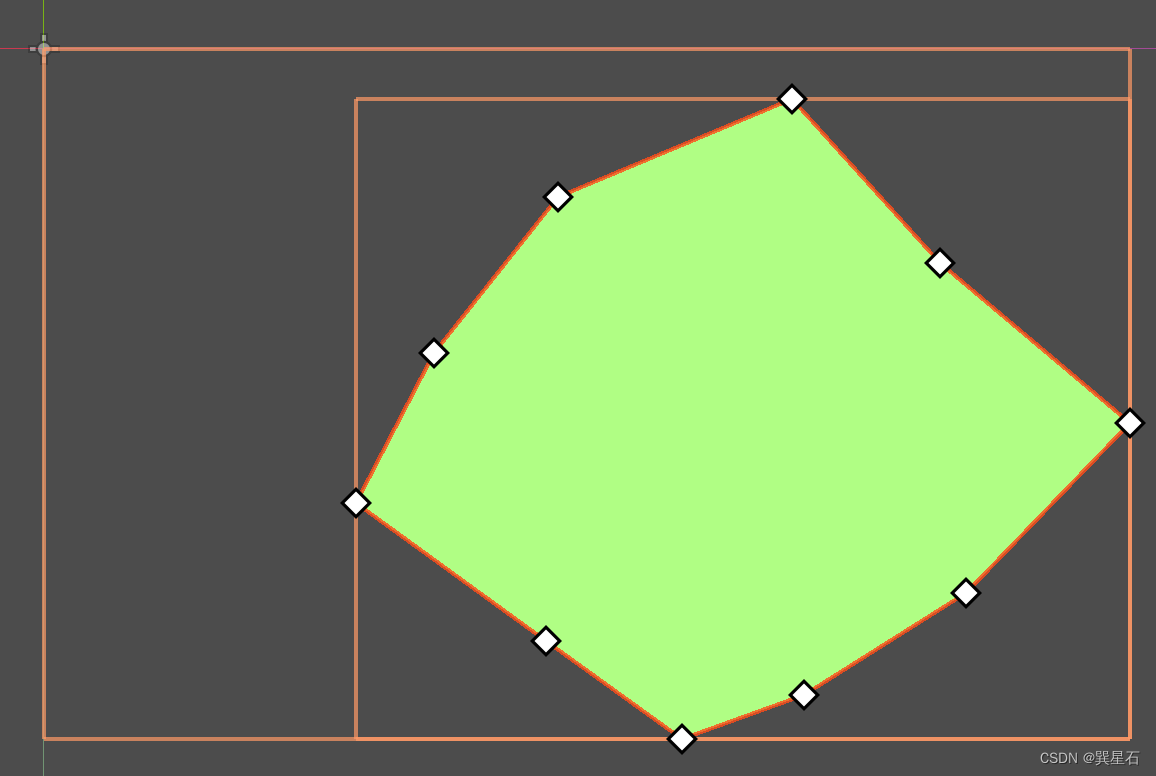
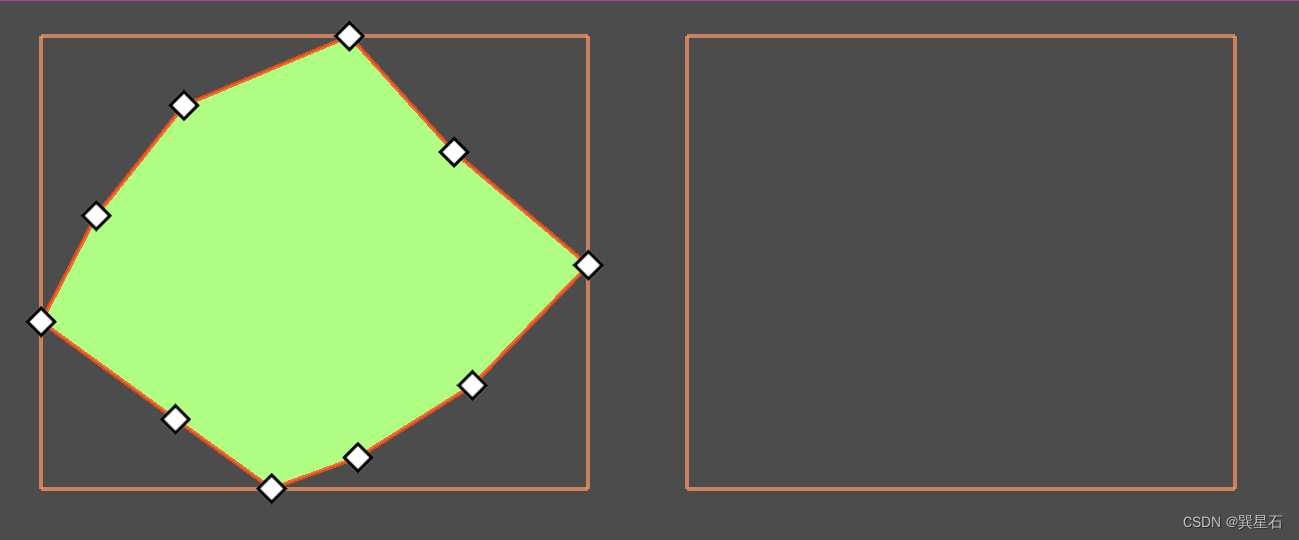
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
当然，上面的代码只是展示了求取的思路，实际上，我们只需要一个函数，直接返回Rect2就行。

# 求任意多边形包围盒Rect2
func get_polygon_Rect2(polygon:PackedVector2Array) -> Rect2:
	var xs = [];var ys = []  # 所有的x和y
	# 遍历所有顶点，抽离出所有的x和y坐标到单独的数组
	for i in range(polygon.size()):
		xs.append(polygon[i].x);ys.append(polygon[i].y)
	# 升序排列
	xs.sort();ys.sort()
	# 获取 position
	var pos = Vector2(xs[0],ys[0]) # Rect2.position
	# 降序排列
	xs.reverse();ys.reverse()
	# 获取 end
	var end = Vector2(xs[0],ys[0]) # Rect2.end
	# 获取 size
	var size = end - pos if end > pos else pos -end  # 计算 Rect2.size
	return  Rect2(pos,size)

测试：

var p1 = polygon1.polygon
var rect = get_polygon_Rect2(p1)
print(rect.position)
print(rect.size)
print(rect.end)
print(rect.get_center())

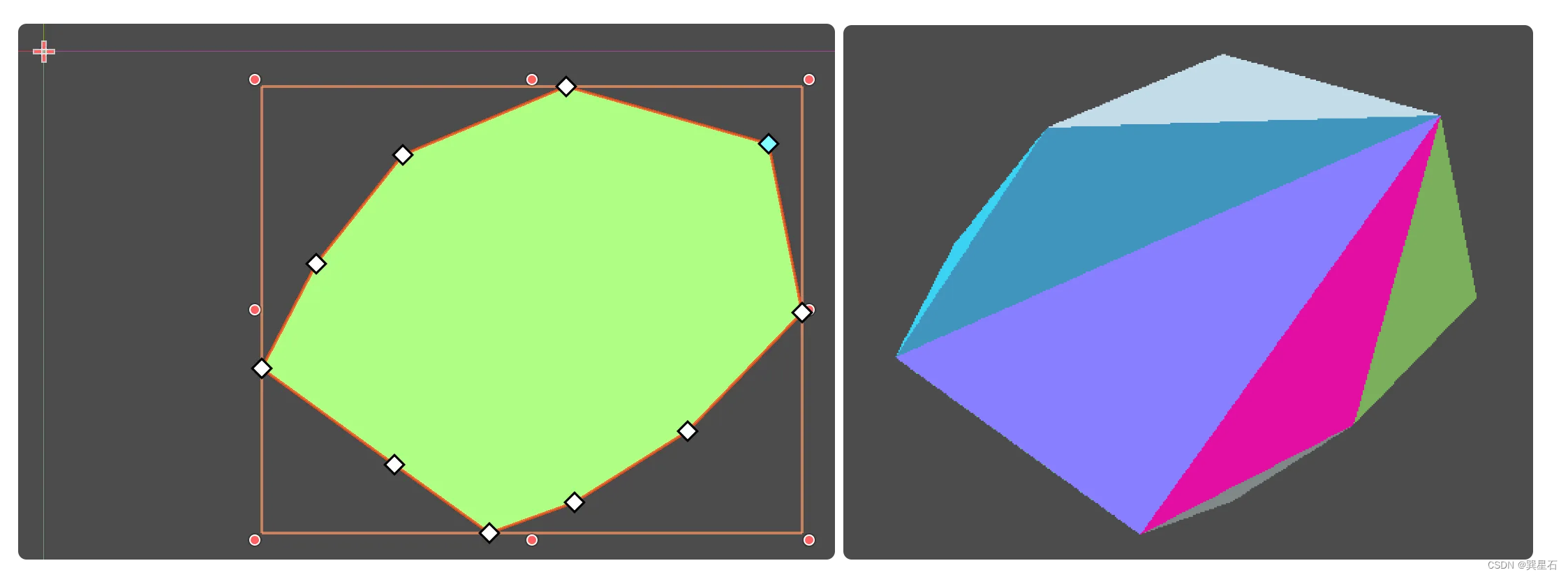
对多边形进行三角化

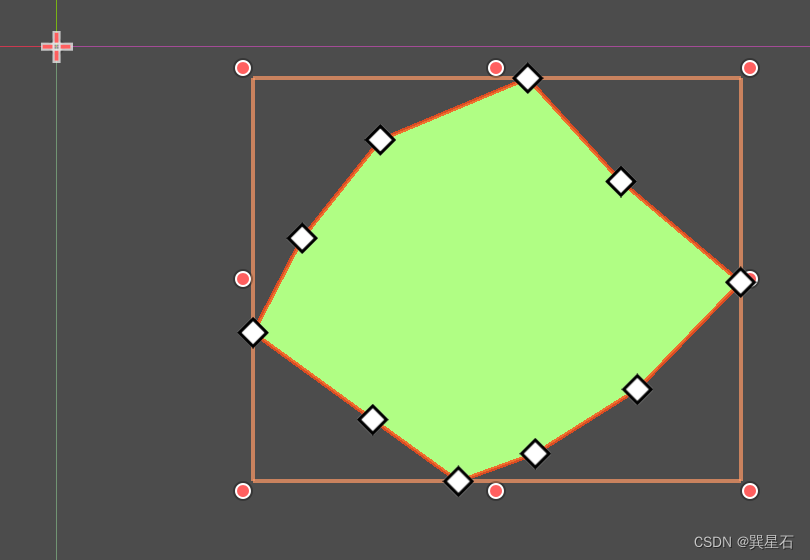
在这里插入图片描述

extends Node2D

@onready var polygon1 = $Polygon1

func _ready():
	var p1 = polygon1.polygon
	print(Geometry2D.triangulate_delaunay(p1))

打印内容：

[1, 2, 3, 2, 3, 4, 3, 4, 5, 3, 5, 6, 6, 7, 8, 1, 3, 8, 3, 6, 8, 0, 1, 8, 0, 8, 9]

其中的数字代表的是多边形的顶点索引，每三个顶点构成一个三角形。所以返回的元素数目肯定是3的整数倍。

我们编写一个函数来获得所有三角形的数据。

# 返回多边形三角化后的所有三角形数据
func polygon_triangles(polygon:PackedVector2Array) -> Array[PackedVector2Array]:
	var arr:Array[PackedVector2Array] = []
	var indexs = Geometry2D.triangulate_delaunay(polygon)
	print(indexs)
	for i in range(indexs.size()/3):
		var tag_index = indexs.slice(3 * i,3 * i + 3) 
		var tag:PackedVector2Array = []
		tag.append(polygon[tag_index[0]])
		tag.append(polygon[tag_index[1]])
		tag.append(polygon[tag_index[2]])
		arr.append(tag)
	return arr

通过遍历和绘制所有三角形：

extends Node2D

@onready var polygon1 = $Polygon1
var tags:Array[PackedVector2Array]


func _ready():
	var p1 = polygon1.polygon
	tags = polygon_triangles(p1)

func _draw():
	for tag in tags:
		var color = Color(randf(),randf(),randf())
		draw_colored_polygon(tag,color)

绘制出的结果：

在这里插入图片描述
我们使用一个更明显的凹多边形：
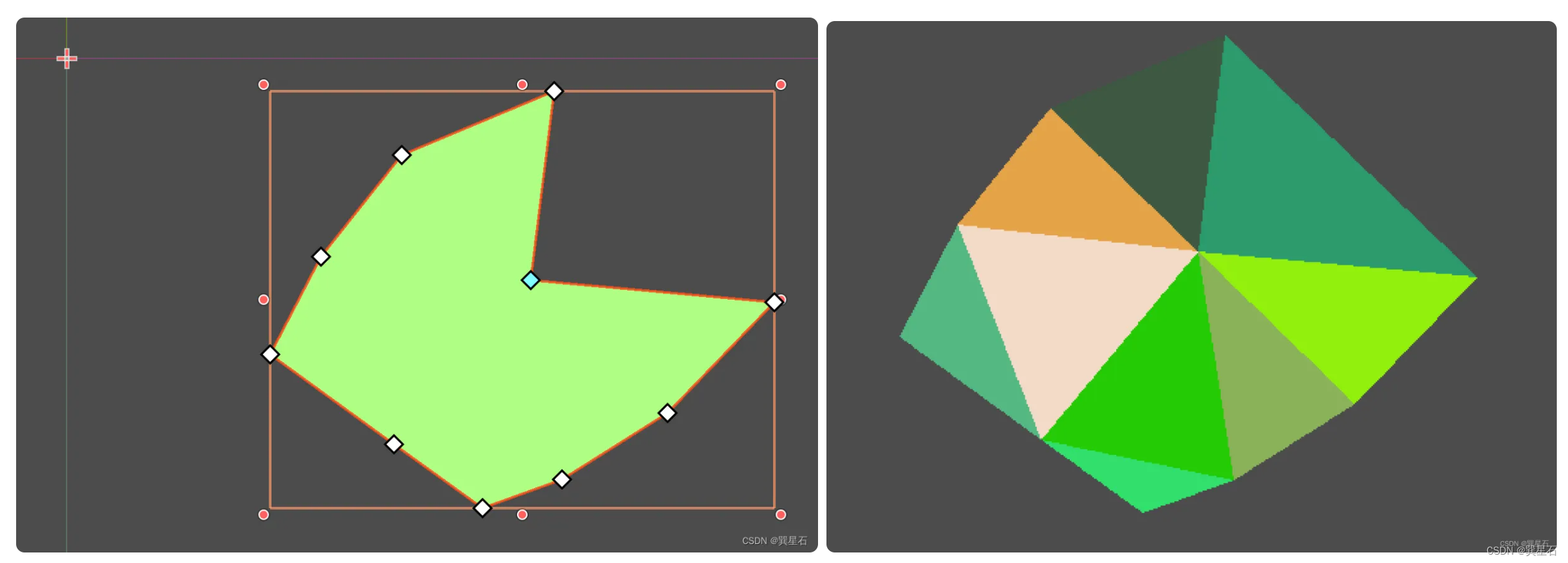
在这里插入图片描述

可以看到，凹多边形三角化后，会填补为一个凸多边形。

如果想要凹多边形得到完全一致的三角化效果，则需要用Geometry2D的triangulate_polygon替代triangulate_delaunay。

之前的自定义函数也就变为了：

# 返回多边形三角化后的所有三角形数据
func polygon_triangles(polygon:PackedVector2Array) -> Array[PackedVector2Array]:
	var arr:Array[PackedVector2Array] = []
	var indexs = Geometry2D.triangulate_polygon(polygon)
	for i in range(indexs.size()/3):
		var tag_index = indexs.slice(3 * i,3 * i + 3) 
		var tag:PackedVector2Array = []
		tag.append(polygon[tag_index[0]])
		tag.append(polygon[tag_index[1]])
		tag.append(polygon[tag_index[2]])
		arr.append(tag)
	return arr

凹多边形返回的三角化效果：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1537813.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

目标控制器数字孪生系统的研究与设计

目标控制器数字孪生系统的研究与设计

文章来源：铁路计算机应用,2023,32(10):36-41. 作者：许婧，杨硕，季志均 摘要：随着目标控制器（OC，Object Controller）系统在轨道交通领域的推广应用，其硬件投入较高、研发…
阅读更多...
css background-color属性无效

css background-color属性无效

因为工作需要&#xff0c;最近在帮H5同事开发几个页面&#xff0c;在使用H5进行如下布局的时候&#xff0c;发现设置 background-color为白色无效。 代码如下&#xff1a; <div class "bottomBar"><div style"position: fixed; left: 20px;">…
阅读更多...
解决arco-design下拉框回显id的问题

解决arco-design下拉框回显id的问题

问题描述 下拉框回显选项中没有的选项&#xff0c;就会出现以下情况&#xff0c;只能把uid回显上去 解决方案 使用ui框架自带的属性fallback-option 用法 按以上操作&#xff0c;即可解决选择框回显uid问题
阅读更多...
软考91-上午题-【操作系统】-线程

软考91-上午题-【操作系统】-线程

一、线程的定义 传统的进程有两个基本属性: 可拥有资源的独立单位&#xff1b;可独立调度和分配的基本单位。 引入线程的原因是进程在创建、撤销和切换中&#xff0c;系统必须为之付出较大的时空开销&#xff0c;故在系统中设置的进程数目不宜过多&#xff0c;进程切换的频率…
阅读更多...
Day43：WEB攻防-PHP应用SQL注入符号拼接请求方法HTTP头JSON编码类

Day43：WEB攻防-PHP应用SQL注入符号拼接请求方法HTTP头JSON编码类

目录 PHP-MYSQL-数据请求类型 PHP-MYSQL-数据请求方法 PHP-MYSQL-数据请求格式 知识点&#xff1a; 1、PHP-MYSQL-SQL注入-数据请求类型 2、PHP-MYSQL-SQL注入-数据请求方法 3、PHP-MYSQL-SQL注入-数据请求格式 PHP-MYSQL-数据请求类型 SQL语句由于在黑盒中是无法预知写法的…
阅读更多...
基于python+vue的BBS论坛系统flask-django-nodejs-php

基于python+vue的BBS论坛系统flask-django-nodejs-php

本系统为用户而设计制作BBS论坛系统&#xff0c;旨在实现BBS论坛智能化、现代化管理。本BBS论坛自动化系统的开发和研制的最终目的是将BBS论坛的运作模式从手工记录数据转变为网络信息查询管理&#xff0c;从而为现代管理人员的使用提供更多的便利和条件。使BBS论坛系统数字化、…
阅读更多...
使用阿里CICD流水线打包Vue项目到阿里的docker镜像私仓，并自动部署到服务器启动服务

使用阿里CICD流水线打包Vue项目到阿里的docker镜像私仓，并自动部署到服务器启动服务

文章目录 使用阿里CICD流水线打包Vue项目到阿里的docker镜像私仓&#xff0c;并自动部署到服务器启动服务1、功能实现原理大家可以看我之前的两篇文章2、打包vue项目和打包咱们的Java项目过程差不多相同&#xff0c;大家可以看着上面的Java打包过程进行实验&#xff0c;下面是v…
阅读更多...
关于短群签名论文阅读

关于短群签名论文阅读

参考文献为2004年发表的Short Group Signatures 什么群签名&#xff1f; 群签名大致就是由一组用户组成一个群&#xff0c;其中用户对某条消息的签名&#xff0c;改签名不会揭示是哪一个用户签署的&#xff0c;签名只能表明该消息确实是来自该群的签名。对于群还有一个群管理者…
阅读更多...
VTK9.2.0+Qt5.14.0 绘制点云

VTK9.2.0+Qt5.14.0 绘制点云

背景 为了显示结构光重建后的点云&#xff0c;开发QT5.14.0VTK9.2.0的上位机软件&#xff0c;用于对结构光3D相机进行控制&#xff0c;并接收传输回来的3D数据&#xff0c;显示在窗口中。 配置QT和VTK VTK9.2.0下载源码&#xff0c;用Cmake编译&#xff0c;编译好的VTK9.2.0…
阅读更多...
Nacos介绍和Eureka的区别

Nacos介绍和Eureka的区别

Nacos&#xff08;全称为 Alibaba Cloud Nacos&#xff0c;或简称为 Nacos&#xff09;是一个开源的分布式服务发现和配置管理系统。它由阿里巴巴集团开发并开源&#xff0c;旨在帮助开发人员简化微服务架构下的服务注册、发现和配置管理。 1、Nacos 提供了以下主要功能&#…
阅读更多...
短视频矩阵系统----源头开发

短视频矩阵系统----源头开发

短视频矩阵源码技术开发要求及实现流程&#xff1a; 短视频矩阵开发要求具备视频录制、编辑、剪辑、分享等基本功能&#xff0c;支持实时滤镜、特效、音乐等个性化编辑&#xff0c;能够实现高效的视频渲染和处理。开发流程主要包括需求分析、技术选型、设计架构、编码实现、测试…
阅读更多...
Binance labs孵化的Swan Chain明牌空投测试网零撸教程

Binance labs孵化的Swan Chain明牌空投测试网零撸教程

简介&#xff1a;Swan Chain 是一个 Layer2云计算网络&#xff0c;可以将数据、计算、带宽和支付集成到一个套件&#xff0c;为Web3项目提供全面的解决方案。 相关概念&#xff1a;云计算、layer2、infrastructure 融资信息&#xff1a;项目在去年获得bi’an领投的300万美元融…
阅读更多...
Flask 与小程序 的图片数据交互 过程及探讨研究学习

Flask 与小程序 的图片数据交互 过程及探讨研究学习

今天不知道怎么的&#xff0c;之前拿编程浪子地作品抄过来粘上用好好的&#xff0c;昨天开始照片突的就不显示了。 今天不妨再耐味地细细探究一下微信小程序wxml 和flask服务器端是怎么jpg图片数据交互的。 mina/pages/food/index.wxml <!--index.wxml--> <!--1px …
阅读更多...
深度学习知识【CSPNet网络详解】

深度学习知识【CSPNet网络详解】

CSPNet的贡献 1.增强了CNN的学习能力&#xff0c;能够在轻量化的同时保持准确性。 2.降低计算瓶颈。 3.降低内存成本。 CSPNet介绍 在神经网络推理过程中计算量过高的问题是由于网络优化中的梯度信息重复导致的。CSPNet通过将梯度的变化从头到尾地集成到特征图中&#xff0c…
阅读更多...
Golang案例开发之gopacket抓包三次握手四次分手（3）

Golang案例开发之gopacket抓包三次握手四次分手（3）

文章目录 前言一、理论知识三次握手四次分手二、代码实践1.模拟客户端和服务器端2.三次握手代码3.四次分手代码验证代码完整代码总结前言 TCP通讯的三次握手和四次分手，有很多文章都在介绍了，当我们了解了gopacket这个工具的时候，我们当然是用代码实践一下，我们的理论。本…
阅读更多...
如何在linux环境上部署单机ES（以8.12.2版本为例）

如何在linux环境上部署单机ES（以8.12.2版本为例）

ES安装&#xff08;以8.12.2版本为例&#xff09; 首先创建好对应的文件夹然后在对应的文件夹下执行依次这些命令 1.wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-8.12.2-linux-x86_64.tar.gz 2.wget https://artifacts.elastic.co/downloads/…
阅读更多...
002_avoid_for_loop_in_Matlab避免使用for循环

002_avoid_for_loop_in_Matlab避免使用for循环

避免使用for循环 在程序设计思想中&#xff0c;循环是一个很有力的工具。在循环中&#xff0c;计算机很轻松地重复执行相同的操作。循环是汇编之上的编程中最重要的概念之一。Matlab的循环有两个语言构造&#xff0c;一个是for循环&#xff0c;另一个是while循环。在Matlab中&…
阅读更多...
Git原理及使用

Git原理及使用

1、Git初识 Git是一种版本控制器： 对于同一份文件，做多次改动，Git会记录每一次改动前后的文件。 通俗的讲就是⼀个可以记录⼯程的每⼀次改动和版本迭代的⼀个管理系统，同时也⽅便多⼈协同作业。 注意： Git其实只能跟踪⽂本⽂件的改动，⽐如TXT⽂件，⽹⻚，所有的程序代码…
阅读更多...
基于docker配置pycharm开发环境

基于docker配置pycharm开发环境

开发过程中&#xff0c;为了做好环境隔离&#xff0c;经常会采用docker来进行开发&#xff0c;但是如何快速将docker中的环境和本地开发的IDE链接起来是一个常见问题&#xff0c;下面对其进行简单的总结&#xff1a; &#xff08;1&#xff09;前期准备 开发环境docker和工具p…
阅读更多...
【练习】双指针算法思想

【练习】双指针算法思想

&#x1f3a5; 个人主页&#xff1a;Dikz12&#x1f525;个人专栏&#xff1a;Java算法&#x1f4d5;格言&#xff1a;那些在暗处执拗生长的花&#xff0c;终有一日会馥郁传香欢迎大家&#x1f44d;点赞✍评论⭐收藏 目录 1. 移动零 1.1 题目描述 1.2 讲解算法原理 1.3 编…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023