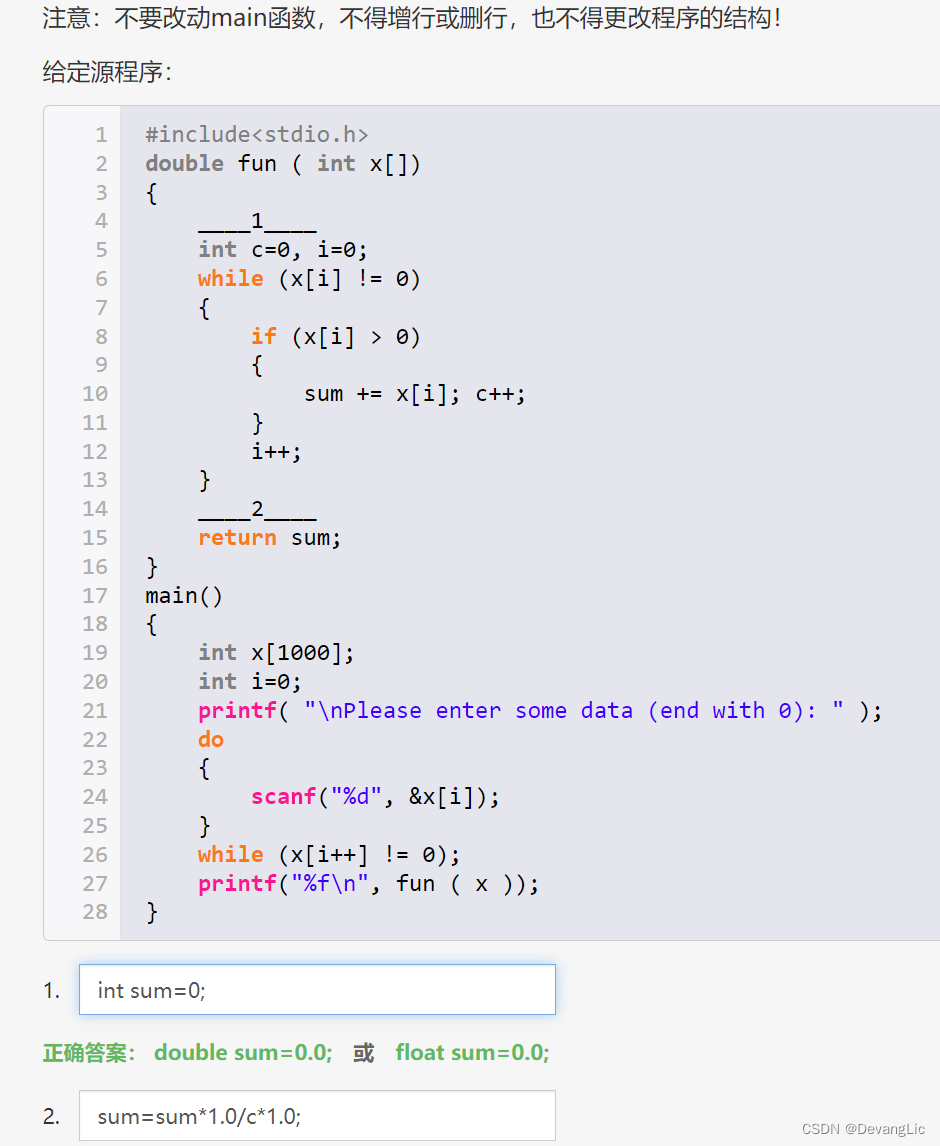
地理坐标系与UTM坐标系转换并进行gazebo测试

经纬度到UTM坐标的转换
- gazebo测试环境

在这里插入图片描述
全球卫星导航系统(Global Navigation Satelite System,GNSS)，简称卫星导航，是室外机器人定位的一个主要信息来源。

卫星导航能给机器人提供什么信息？
正常工作时，实际上可以提供机器人所需的所有定位信息，包括：

位置
姿态
速度等物理量

但是仅依靠卫星导航还不足以让机器人在室外完成自主导航任务，主要原因有一下几点：

GNSS提供的定位精度不能满足要求，GNSS分多个细分种类，有些GNSS定位方法可以提供很高的精度，但要求物体必须静止一段时间（通常十分钟以上）；也有的方法可以提供较好的动态物体定位，但需要事先架设一个或多个基站。
GNSS的定位频率不能满足要求，一般在5-10hz
GNSS定位可用性存在问题，不能够全天候、全场地使用，稳定性与场景、结构、物体的遮挡关系，甚至和天气有关。

GNSS定位原理：
GNSS通过测量自身与地球周围各卫星的距离来确定自身位置，与卫星的距离主要通过测量时间间隔来确定。一个卫星信号从卫星上发出时，带有一个发送时间,而GNSS接收机接收到它时，有一个接收时间，通过比较时间间隔，就能估算各卫星离我们的距离。GNSS本质上可以看成一种高精度的授时系统。

在这里插入图片描述

经纬度到UTM坐标的转换

一般的单点GNSS或者RTK都会输出接收器测量到的经纬度。

下面通过程序将测量到的经纬度转换为米制的UTM坐标。

有的RTK带有双天线，在测量经纬度的同时，还可以输出方向角，如果不考虑机器人的俯仰和横滚，将它们视为零。即可以将双天线RTK输出的四自由度坐标，在假设机器人的俯仰和横滚为零的前提下，可以把RTK输出视为六自由度的位置变换，即SE(3)的位姿。

经纬度转UTM的算法比较复杂和琐碎，使用一个开源的转换方法来实现这部分内容。

gazebo测试环境

在飞机上添加一个GPS模块

  <!-- Mount an  Default GPS. -->
  <xacro:default_gps namespace="${namespace}" parent_link="${namespace}/base_link" />

默认的GPS 用的 rotors_simulator的 gps 插件，可以设置水平、垂直位置精度，水平垂直速度精度

  <xacro:macro name="default_gps" params="namespace parent_link">
    <!-- Default GPS. -->
    <xacro:gps_plugin_macro
      namespace="${namespace}"
      gps_suffix=""
      parent_link="${parent_link}"
      gps_topic="gps"
      ground_speed_topic="ground_speed"
      mass_gps_sensor="0.015"
      horizontal_pos_std_dev="3.0"
      vertical_pos_std_dev="6.0"
      horizontal_vel_std_dev="0.1"
      vertical_vel_std_dev="0.1">
      <inertia ixx="0.00001" ixy="0.0" ixz="0.0" iyy="0.00001" iyz="0.0" izz="0.00001" />
      <origin xyz="0 0 0" rpy="0 0 0" />
    </xacro:gps_plugin_macro>
  </xacro:macro>

设置好后，启动gazebo

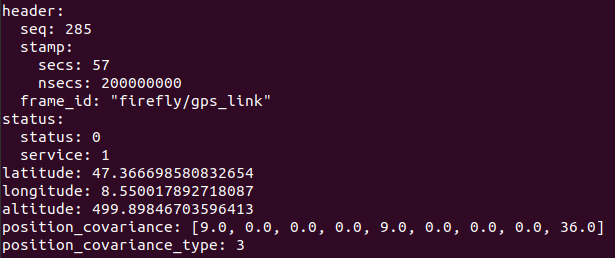
打印gps发出的数据如下

header:
seq: 285
stamp:
secs: 57
nsecs: 200000000
frame_id: “firefly/gps_link”
status:
status: 0
service: 1
latitude: 47.366698580832654
longitude: 8.550017892718087
altitude: 499.89846703596413
position_covariance: [9.0, 0.0, 0.0, 0.0, 9.0, 0.0, 0.0, 0.0, 36.0]
position_covariance_type: 3

经纬度转UTM坐标

bool LatLon2UTM(const Vec2d& latlon, UTMCoordinate& utm_coor) {
    long zone = 0;
    char char_north = 0;
    long ret = Convert_Geodetic_To_UTM(latlon[0] * math::kDEG2RAD, latlon[1] * math::kDEG2RAD, &zone, &char_north,
                                       &utm_coor.xy_[0], &utm_coor.xy_[1]);
    utm_coor.zone_ = (int)zone;
    utm_coor.north_ = char_north == 'N';

    return ret == 0;
}

输入向量 Vec2d 就是 Eigen::Vector2d 的经纬度值
输出 UTMCoordinate格式的 utm数据，UTMCoordinate格式定义如下：

/// UTM 坐标
struct UTMCoordinate {
    UTMCoordinate() = default;
    explicit UTMCoordinate(int zone, const Vec2d& xy = Vec2d::Zero(), bool north = true)
        : zone_(zone), xy_(xy), north_(north) {}

    int zone_ = 0;              // utm 区域
    Vec2d xy_ = Vec2d::Zero();  // utm xy
    double z_ = 0;              // z 高度（直接来自于gps）
    bool north_ = true;         // 是否在北半球
};

其中调用了 Convert_Geodetic_To_UTM 函数是调用的 utm_convert库中的函数
参数解释如下

     *    Latitude          : Latitude in radians                 (input)
     *    Longitude         : Longitude in radians                (input)
     *    Zone              : UTM zone                            (output)
     *    Hemisphere        : North or South hemisphere           (output)
     *    Easting           : Easting (X) in meters               (output)
     *    Northing          : Northing (Y) in meters              (output)

输出结果

        std::cout<< "utm zone:  " <<utm_coor.zone_<<std::endl;
        std::cout<< "utm x:  " <<utm_coor.xy_[0]<<std::endl;
        std::cout<< "utm y:  " <<utm_coor.xy_[1]<<std::endl;

其中的一帧转换值

utm zone: 32
utm x: 466024
utm y: 5.24601e+06

也就是说
latitude: 47.366698580832654
longitude: 8.550017892718087
转到UTM坐标系约为
zone: 32
x: 466024
y: 5.24601e+06

可以看到x 和 y的数值很大，不好进行判断，一般把获取第一帧数据位置标为零点，也就是后面的数据都减去起始位置

代码如下：

        sensor_msgs::NavSatFix Gps = *Gps_msg;
        Vec2d gps_latlon;
        UTMCoordinate utm_coor;
        static bool first_gnss_set = false;
        static Vec2d origin = Vec2d::Zero();
        
        gps_latlon[0] = Gps.latitude;
        gps_latlon[1] = Gps.longitude;
        LatLon2UTM(gps_latlon,utm_coor);

        if (!first_gnss_set) {
            origin << utm_coor.xy_[0],utm_coor.xy_[1];
            first_gnss_set = true;
        }
        utm_coor.xy_ = utm_coor.xy_ - origin;

上面是机器人上最简单的获得卫星导航位置的情况，该情况上默认导航的GPS或RTK安装在机器人的正中心位置。

下面介绍复杂一些的情况：GPS的位置与机器人中心有偏差。
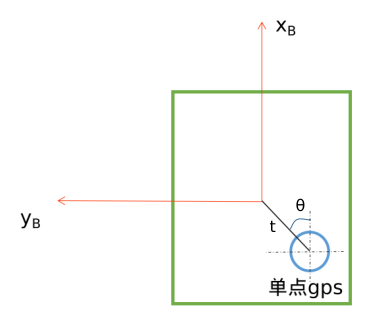
在这里插入图片描述

还有另一种情况，RTK可以输出双天线的角度，双天线也不与机器人前向一致。
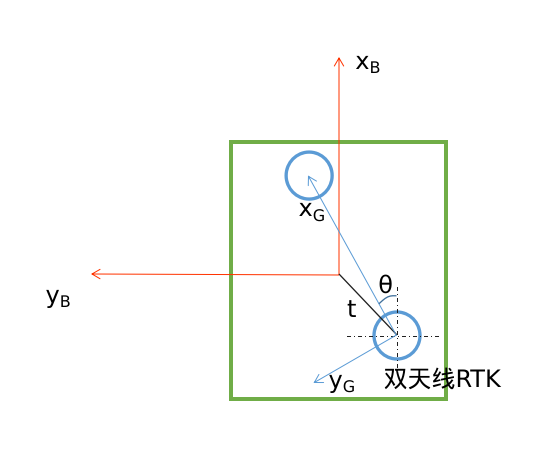
在这里插入图片描述
上面的图中，红色坐标代表机器人坐标系，蓝色代表GNSS坐标系。

双天线RTK输出的UTM坐标和方向角的读数，可视为 $T_{WG}$ ,其中W代表世界坐标系，G代表GNSS坐标系。

机器人需要的导航定位数据为 $T_{WB}$ ，其中B为机器人坐标系。

为了将RTK输出的 $T_{WG}$ 转为机器人需要的导航定位数据为 $T_{WB}$ ，则需进行GNSS接收器与机器人中心的外参，来组成 $T_{BG}$ 。

在参数标定中，可以规定如下：
指定安装偏移量 $t$ ,为 $O_{B}$ 指向 $O_{G}$ 的矢量，在B系中取坐标，这就是 $T_{BG}$ 的平移分量。
指定安装偏角 $\theta$ ，为B系的x轴转向G系x轴之间的转角，这就是 $T_{BG}$ 的旋转分量。
得到转换矩阵 $T_{BG}$ 为：
$T_{BG}=\begin{bmatrix} R_{Z}(\theta ) & t\\ 0 &1 \end{bmatrix}$

机器人坐标系到世界坐标系的变化矩阵 $T_{WB}$ ，最终由RTK的读数和标定的外参计算可得为：
$T_{WB}=T_{WG}T_{GB}$
分开写为：
$R_{WB}=R_{WG}R_{GB} , t_{WB}=R_{WG}t_{GB}+t_{WG}$

代码如下：
将方法构造成一个函数
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

bool ConvertGps2UTM(GNSS& gps_msg, const Vec2d& antenna_pos, const double& antenna_angle, const Vec3d& map_origin)

其中第一个参数 GNSS 其结构体定义如下：

/// 一个GNSS读数结构
struct GNSS {
    GNSS() = default;
    GNSS(double unix_time, int status, const Vec3d& lat_lon_alt, double heading, bool heading_valid)
        : unix_time_(unix_time), lat_lon_alt_(lat_lon_alt), heading_(heading), heading_valid_(heading_valid) {
        status_ = GpsStatusType(status);
    }

    double unix_time_ = 0;                                  // unix系统时间
    GpsStatusType status_ = GpsStatusType::GNSS_NOT_EXIST;  // GNSS 状态位
    Vec3d lat_lon_alt_ = Vec3d::Zero();                     // 经度、纬度、高度，前二者单位为度
    double heading_ = 0.0;                                  // 双天线读到的方位角，单位为度
    bool heading_valid_ = false;                            // 方位角是否有效

    UTMCoordinate utm_;       // UTM 坐标（区域之类的也在内）
    bool utm_valid_ = false;  // UTM 坐标是否已经计算（若经纬度给出错误数值，此处也为false）

    SE3 utm_pose_;  // 用于后处理的6DoF Pose
};

第二个参数是安装偏移量，第三个参数是安装偏移角度，第四个参数是地图原点。

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
经纬高转换为UTM

    UTMCoordinate utm_rtk;
    if (!LatLon2UTM(gps_msg.lat_lon_alt_.head<2>(), utm_rtk)) {
        return false;
    }
    utm_rtk.z_ = gps_msg.lat_lon_alt_[2];

用之前介绍的的LatLon2UTM函数
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
如果卫星导航方案是双天线RTK则数据中带有方位角信息，根据方位角信息是否效，来设置rtk方位角
有的rtk的方位角是北东地坐标系，如果转成东北天坐标系则需要进行一个转换
一个北东地坐标系的方位角h,转换到东北天坐标系下的角度 $h^{’}$ 的转换公式为：
$h^{’} =\pi /2-h$

    /// RTK heading 转成弧度
    double heading = 0;
    if (gps_msg.heading_valid_) {
        heading = (90 - gps_msg.heading_) * math::kDEG2RAD;  // 北东地转到东北天
    }

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
构建卫星导航坐标系到机器人坐标系的转换矩阵，根据外参的测量结果

此时存在两种情况，第一种双天线RTK，存在安装偏移量与安装偏移角度。

    SE3 TBG(SO3::rotZ(antenna_angle * math::kDEG2RAD), Vec3d(antenna_pos[0], antenna_pos[1], 0));
    SE3 TGB = TBG.inverse();

其中 antenna_angle 就是安装偏移角度，是机器人坐标系x轴转向卫星导航坐标系x轴之间的转角
antenna_pos 就是安装偏移量，是机器人坐标系原点指向卫星导航坐标系原点的矢量，在机器人坐标系中取坐标

然后就可以求得 $T_{WB}$

        // 若指明地图原点，则减去地图原点
        double x = utm_rtk.xy_[0] - map_origin[0];
        double y = utm_rtk.xy_[1] - map_origin[1];
        double z = utm_rtk.z_ - map_origin[2];
        SE3 TWG(SO3::rotZ(heading), Vec3d(x, y, z));
        TWB = TWG * TGB;

另一种情况，单点GPS，存在安装偏移量，但是单点GPS不输出方位角，没有卫星导航坐标系，仅有机器人坐标系到GPS中心的角度
需要通过状态估计算法得到的机器人姿态的方位角直接构成 $R_{WB}$ ，此时还需要设置一个 $R_{BG}$ ，因为没有偏移角度，所以说叫设置一个，比如就认为B系和G系的方向一致，那么 $R_{BG} = I$ ,然后再得到 $R_{WG}$ 。

        // 单点gps方案情况
        float uav_yaw;
        SO3 RWB = SO3::rotZ(uav_yaw * math::kDEG2RAD);
        SO3 RBG = SO3::rotZ(0 * math::kDEG2RAD);
        SO3 RWG = RWB*RBG;
        // 若指明地图原点，则减去地图原点
        double x = utm_rtk.xy_[0] - map_origin[0];
        double y = utm_rtk.xy_[1] - map_origin[1];
        double z = utm_rtk.z_ - map_origin[2];
        SE3 TWG(RWG, Vec3d(x, y, z));
        SE3 TBG(RBG,Vec3d(antenna_pos[0], antenna_pos[1], 0));
        SE3 TGB = TBG.inverse();
        TWB = TWG * TGB;

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
然后则对gps结构体中utm的坐标进行赋值即可

    gps_msg.utm_valid_ = true;
    gps_msg.utm_.xy_[0] = TWB.translation().x();
    gps_msg.utm_.xy_[1] = TWB.translation().y();
    gps_msg.utm_.z_ = TWB.translation().z();
    
    if (gps_msg.heading_valid_) {
        // 组装为带旋转的位姿
        gps_msg.utm_pose_ = TWB;
    } else {
        // 组装为仅有平移的SE3
        // 注意当安装偏移存在时，并不能实际推出车辆位姿
        gps_msg.utm_pose_ = SE3(SO3(), TWB.translation());
    }

在gazebo中，设置gps在中心位置，那么则可以设置偏移量和偏移角度为0，然后设置起点位置为原点。

添加路径显示

        geometry_msgs::PoseStamped pose_stamped;

        pose_stamped.header.stamp = ros::Time::now();
        pose_stamped.header.frame_id = "/local_frame";
        pose_stamped.pose.position.x = gps_msg.utm_.xy_[0];
        pose_stamped.pose.position.y = gps_msg.utm_.xy_[1];
        pose_stamped.pose.position.z = gps_msg.utm_.z_;

        pose_stamped.pose.orientation.x = 0;
        pose_stamped.pose.orientation.y = 0;
        pose_stamped.pose.orientation.z = 0;
        pose_stamped.pose.orientation.w = 1;

        UavGpsPath_.poses.push_back(pose_stamped);

        UavGpsPath_.header.stamp = ros::Time::now();
        UavGpsPath_.header.frame_id = "/local_frame";

        GPS_Path_pub_.publish(UavGpsPath_);

模拟场gps定位精度好，rtk的水平定位精度可以到达2cm，垂直6cm
设置gps的定位噪声如下：

      horizontal_pos_std_dev="0.02"
      vertical_pos_std_dev="0.06"

在这里插入图片描述
随便飞了一个轨迹

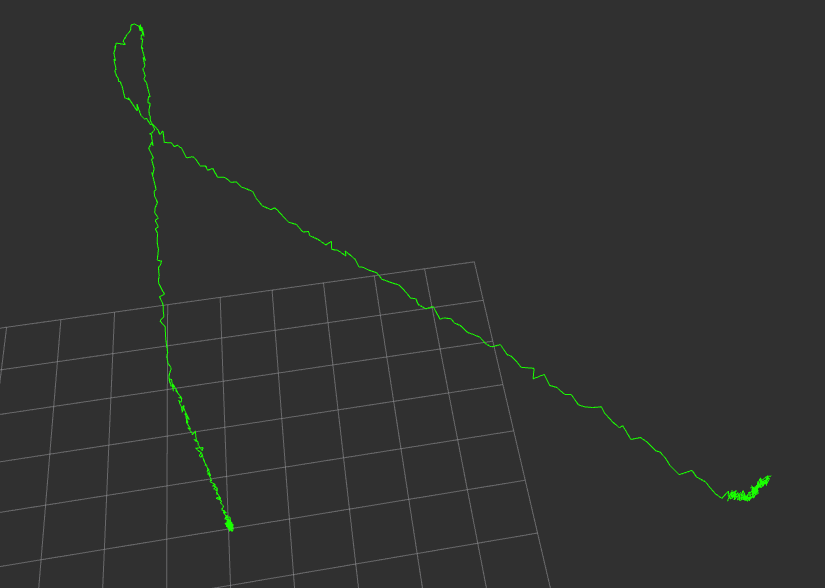
前面场景下的gps定位效果好的情况下，如果gps定位的精度不高，则会出现下面的情况

      horizontal_pos_std_dev="0.2"
      vertical_pos_std_dev="0.4"

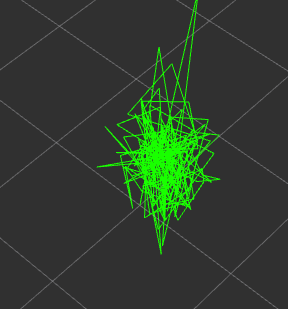
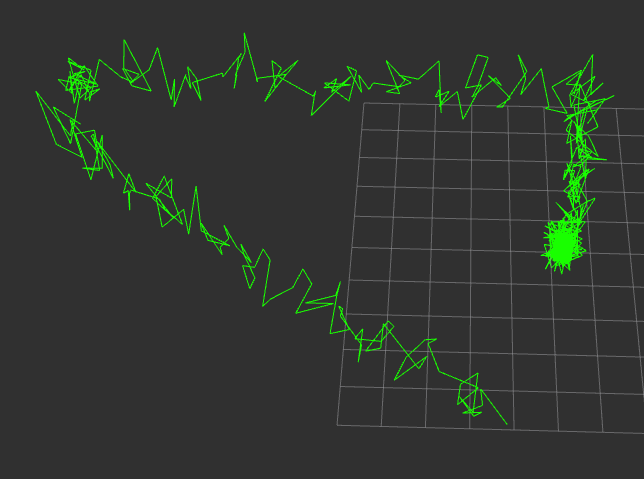
在这里插入图片描述

在这里插入图片描述
由于GPS输出的频率低，并且在信号不好的情况下，会出现较大的噪声，所以并不能直接用于机器人导航，一般会和IMU进行融合，实现组合导航。