堆（详解+例题）

news2025/11/4 20:32:09

一、定义

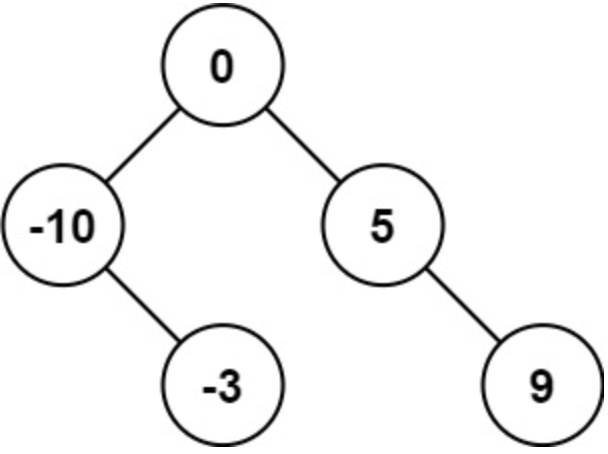
维护一个数据集合，堆是一个完全二叉树。

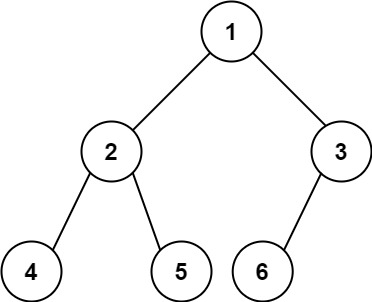
那么什么是二叉树呢？

如图：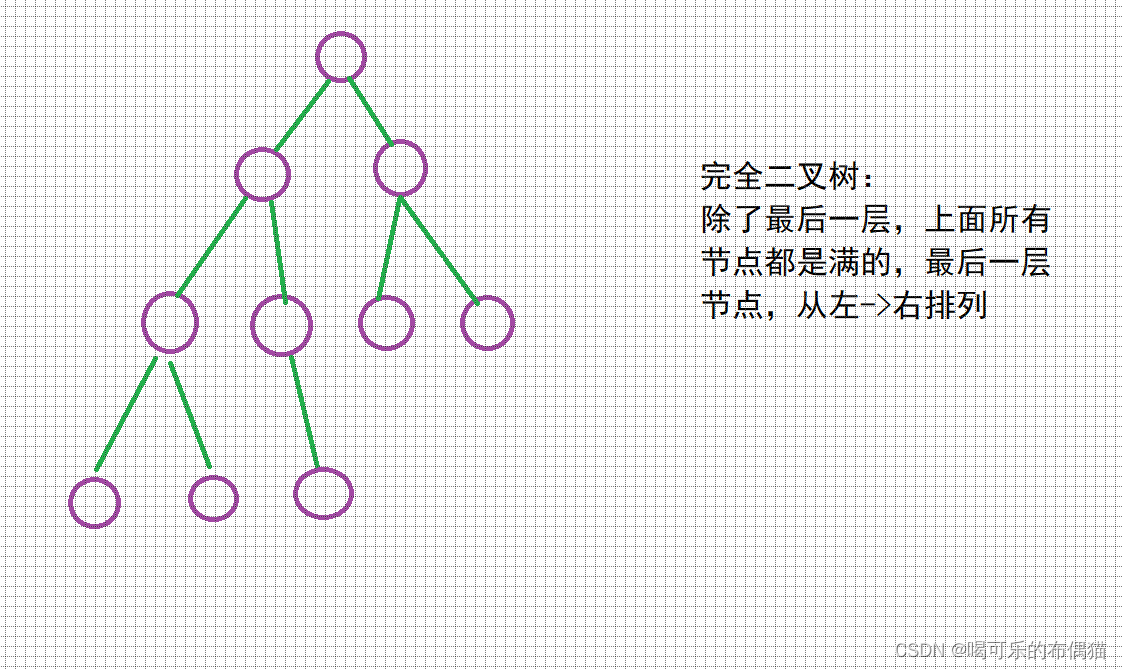

二、关于小根堆实现

性质：每个根节点都小于等于左右两边，所以树根为最小值。

2.1、堆存储（用一维数组来存）

记住规则：x(根)的左儿子 = x * 2;

x(根)的右儿子 = x * 2 + 1

样例如图：

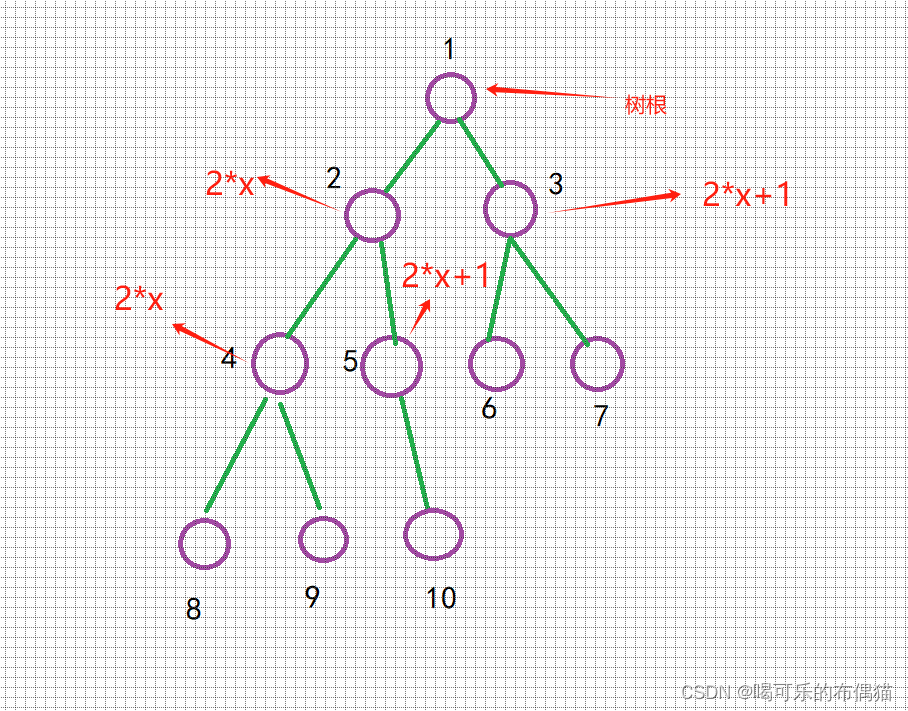
2.2、操作

2.2.1、操作1、down(x) :节点下移

如果把一个值变大了，就让他往下移动。

样例：

2.2.2、操作2、 up(x):节点向上移

如果把某一个值变小了，就让他向上移动

样例：

2.3、如何手写一个堆？

注意：下标要从1开始，heap[]堆，size:堆长度

如图：

这里后面会有对应的例题，详细解释4、5操作

三、例题：

3.1、堆排序：此题来源于acwing

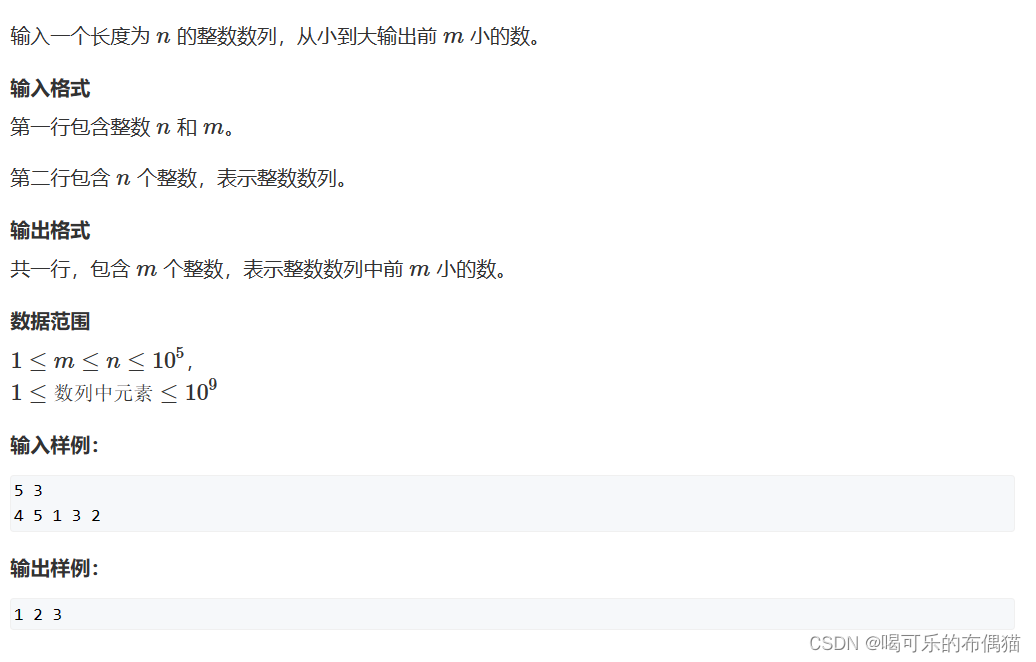
图解：

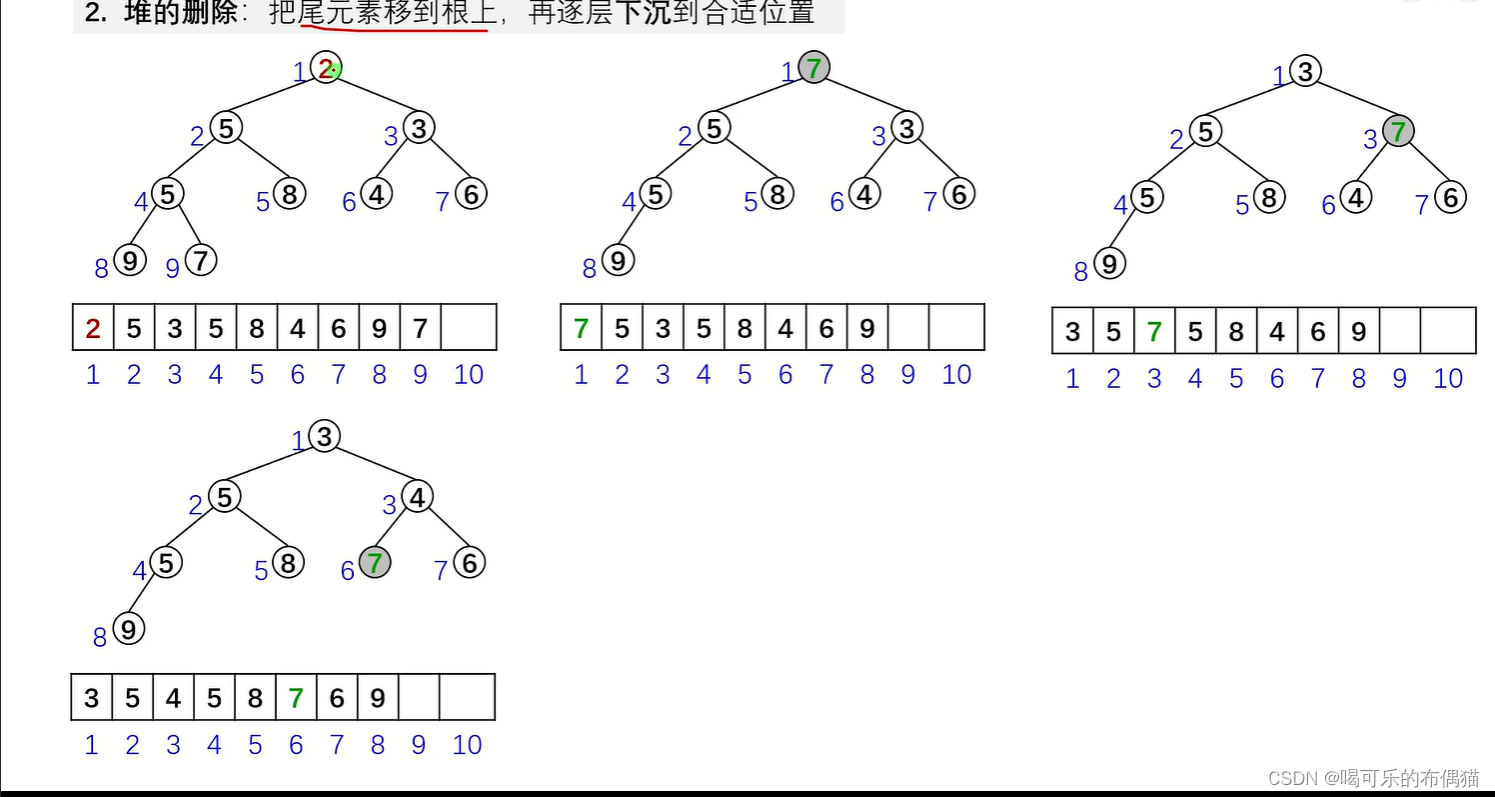上述两个图来自于B站董晓算法的视频

AC代码：

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5+10;
int h[N],sz;
int n,m;

void down(int u)
{
    int t = u;
    if(u*2 <= sz && h[u*2] < h[t]) t = u * 2;
    if(u*2+1 <= sz && h[u*2+1] < h[t]) t = u * 2 + 1;
    if(t != u)
    {
        swap(h[t],h[u]);
        down(t);
    }
}

int main()
{
    scanf("%d %d", &n, &m);
    for(int i=1;i<=n;i++) scanf("%d ",&h[i]);
    sz = n;
    //构建堆，从n/2序号开始创建，把最小值挪到树根,相当于忽略最后一层
    for(int i=n/2;i>=1;i--)
    {
        down(i);
    }
    while (m -- )
    {
        printf("%d ",h[1]);
        h[1] = h[sz];
        sz--;
        down(1);
    }
    return 0;
}

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5+10;
int h[N],sz;
int n,m;
//下沉
void down(int u)
{
    int t = u;
    //根据小根堆性质，保证父亲节点是小于左右两个儿子的
    if(u*2 <= sz && h[u*2] < h[t]) t = u * 2;
    if(u*2+1 <= sz && h[u*2+1] < h[t]) t = u * 2 + 1;
    if(t != u)
    {
        swap(h[t],h[u]);//如果不同，需要交换两个节点
        down(t);//继续下沉
    }
}

int main()
{
    scanf("%d %d", &n, &m);
    for(int i=1;i<=n;i++) scanf("%d ",&h[i]);
    sz = n;//记得传一下长度给sz。
    //构建堆，从n/2序号开始创建，把最小值挪到树根,相当于忽略最后一层
    for(int i=n/2;i>=1;i--)
    {
        //这里非常巧妙，从后面开始去下沉，等到树根的时候，会第一个开始down，
        //会排好，不用担心乱序
        down(i);
    }
    while (m -- )
    {
        printf("%d ",h[1]);//取出最小值
        h[1] = h[sz]; //根据规则操作后续步骤
        sz--;
        down(1);
    }
    return 0;
}

3.2、模拟堆：此题同样来源于acwing

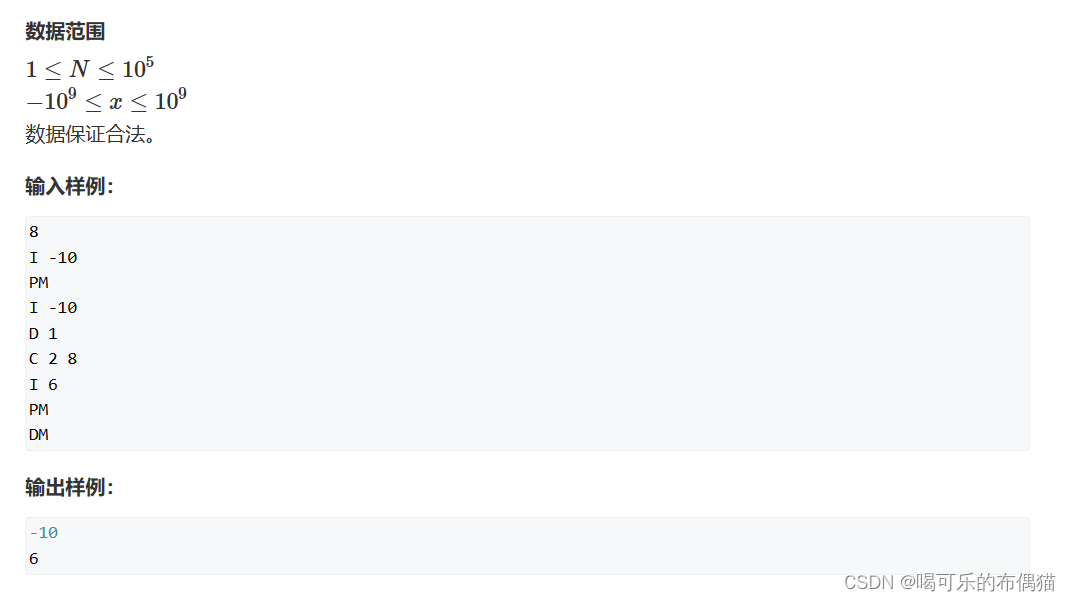
思路：

由于，此题需要记录一下第k个插入的数，所以需要用两个映射的数组去维护一下第k个插入的数，和当前堆中元素的下标，此处附上一位acwing评论区的一位大佬的讲解，我觉得讲的非常好，可以帮助此题理解两个数组的含义，建议先看代码，再看这个。代码中有详细注释，如果有错误欢迎指出~。

AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 1e5+10;
//h[]用来存堆，ph[]用来存第k个数对应的堆里的下标
//hp[]用来存堆下标下是第几个存入的数
int h[N],ph[N],hp[N],sz;
int n,m;

void heap_swap(int a,int b)
{
    swap(h[a],h[b]);//交换堆中的两个数值
    swap(hp[a],hp[b]);//在堆中对应的下标下是第几个存入的数，交换一下
    swap(ph[hp[a]],ph[hp[b]]);//交换一下堆中的下标
}
//下沉
void down(int u)
{
    int t = u;
    if(u*2 <= sz && h[u*2] < h[t]) t = u * 2;
    if(u*2+1 <= sz && h[u*2+1] < h[t]) t = u * 2 + 1;
    if(t != u)
    {
        heap_swap(t,u); //由于后面需要找到第k的数，所以不能用普通的交换，需要用我们手写的交换函数
        down(t);//下沉，直到不满足位置
    }
}
//上浮
void up(int u)
{
    //与根部比较，如果父亲大于儿子就需要上浮
    while(u/2 && h[u/2] > h[u]){
        heap_swap(u/2, u);
        u = u/2;
    }
}

int main()
{
    scanf("%d", &n);
    while (n -- )
    {
        char op[10];//根据题目要求输入字符串
        scanf("%s", op);
        if(!strcmp(op,"I"))
        {
            int x;
            scanf("%d", &x);
            m++;//第几个插入的
            sz++;//当前下标
            //ph表示第k插入的数在堆中的下标是多少
            //hp表示该数堆中下标对应第几个插入的数
            ph[m] = sz,hp[sz] = m;
            h[sz] = x;//堆中存入x
            up(sz);//上浮
        }
        else if(!strcmp(op,"PM")) //找到最小的数，就是树根
        {
            printf("%d\n",h[1]);
        }
        else if(!strcmp(op,"DM")) //注意交换后sz--;
        {
            heap_swap(1,sz);
            sz--;
            down(1);
        }
        else if(!strcmp(op,"D")) //删除第k个数
        {
            int k;
            scanf("%d", &k);
            k = ph[k]; //找到第k个数下的堆中的元素下标
            heap_swap(k,sz);
            sz--;
            down(k),up(k);//down和up只会执行一个操作，因为要么大，要么小
        }
        else
        {
            int k,x;
            scanf("%d %d", &k,&x);
            k = ph[k];
            h[k] = x;
            down(k),up(k);//同理
        }
    }
    return 0;
}