四阶Runge-Kutta方法求解高阶微分方程

news2025/11/4 4:18:00

一、经典的Runge-Kutta方法（四级四阶RK方法）

Runge-Kutta法（简写为RK方法）既可达到较高精度，又可避免高阶导数计算。

对微分方程 $\frac{du}{dt}=f(t,u)$ ,在区间 $[t_{n},t_{n+1}]=[t_{n},t_{n}+\Delta t]$ 上的四阶Runge-Kutta方法的公式如下：

$\left\{\begin{matrix} U_{n+1}=U_{n}+\frac{h}{6}(K_{1}+2K_{2}+2K_{3}+K_{4})\\ K_{1}=f(t_{n},U_{n})\\ K_{2}=f(t_{n}+\frac{1}{2}h,U_{n}+\frac{1}{2}hK_{1})\\ K_{3}=f(t_{n}+\frac{1}{2}h,U_{n}+\frac{1}{2}hK_{2})\\ K_{4}=f(t_{n}+h,U_{n}+hK_{3}) \end{matrix}\right. ,h=\Delta t$

二、利用4阶Runge-Kutta方法计算三阶微分方程的数值解

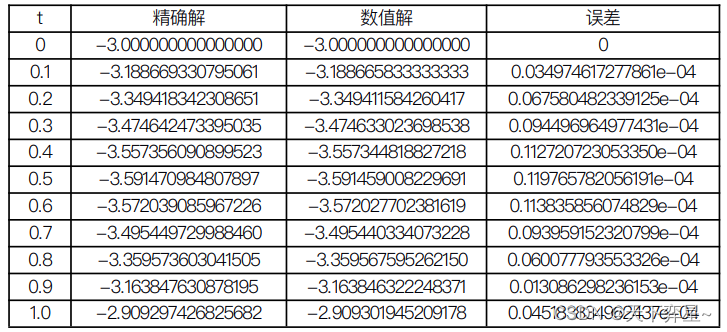
考虑三阶方程的初值问题 $\left\{\begin{matrix} v^{'''}(t)+v^{''}(t)+4v^{'}(t)+4v(t)=4t^{2}+8t-10\\ v(0)=-3,v^{'}(0)=-2,v^{''}(0)=2\\ \end{matrix}\right.$ ，其精确解为 $v(t)=-sin(2t)+t^{2}-3$ ，采用4阶Runge-Kutta法求解上述问题，时间步长取 $\Delta t=0.1$ ，给出 $0\leq t\leq 1$ 的数值解并计算它的误差。

解：

令 $T=\begin{bmatrix} V\\ V^{'}\\ V^{''} \end{bmatrix}$ ,则有

$T^{'}=\begin{bmatrix} V^{'}\\ V^{''}\\ V^{'''} \end{bmatrix}=\begin{bmatrix} 0 &1 & 0\\ 0& 0 & 1\\ -4 & -4 &-1 \end{bmatrix}\begin{bmatrix} V\\ V^{'}\\ V^{''} \end{bmatrix}+\begin{bmatrix} 0\\ 0\\ 4t^{2}+8t-10 \end{bmatrix}$ ，

即

$T^{'}=\begin{bmatrix} V^{'}\\ V^{''}\\ V^{'''} \end{bmatrix}=\begin{bmatrix} 0 &1 & 0\\ 0& 0 & 1\\ -4 & -4 &-1 \end{bmatrix}T+\begin{bmatrix} 0\\ 0\\ 4t^{2}+8t-10 \end{bmatrix}$

这里就将三阶微分方程转换为了一阶微分方程。

format long

%步长
h=0.1;

%节点
X=0:0.1:1;

%节点数
n=length(X);

%计算精确解
exact=zeros(1,n);
exact(1)=-3;
for i=2:n
    exact(i)=-sin(2*X(i))+X(i)^2-3;
end

%定义初值
T0=[-3,-2,2]';

%矩阵A
A=[0,1,0;0,0,1;-4,-4,-1];

%矩阵B
B=@(t) [0,0,4*t^2+8*t-10]';

%采用4阶Runge-Kutta法计算数值解
RK=zeros(3,n);
RK(:,1)=[-3,-2,2]';
for i=2:n
    K1=A*RK(:,i-1)+B(X(i-1));
    K2=A*(RK(:,i-1)+h*K1/2)+B(X(i-1)+h/2);
    K3=A*(RK(:,i-1)+h*K2/2)+B(X(i-1)+h/2);
    K4=A*(RK(:,i-1)+h*K3)+B(X(i-1)+h);
    RK(:,i)=RK(:,i-1)+h*(K1+2*K2+2*K3+K4)/6;
end

%计算误差
error=zeros(1,n);
for i=1:n
    error(i)=exact(i)-RK(1,i);
end

代码运行结果如下：

>> exact

exact =

  列 1 至 8

  -3.000000000000000  -3.188669330795061  -3.349418342308651  -3.474642473395035  -3.557356090899523  -3.591470984807897  -3.572039085967226  -3.495449729988460

  列 9 至 11

  -3.359573603041505  -3.163847630878195  -2.909297426825682

>> RK

RK =

  列 1 至 8

  -3.000000000000000  -3.188665833333333  -3.349411584260417  -3.474633023698538  -3.557344818827218  -3.591459008229691  -3.572027702381619  -3.495440334073228
  -2.000000000000000  -1.760134166666667  -1.442126355739583  -1.050681117543240  -0.593430638007944  -0.080630473086421   0.475249299264954   1.060021210401120
   2.000000000000000   2.794664166666667   3.557647924406250   4.258534364434485   4.869382162297890   5.365839478508025   5.728114760558181   5.941765744667896

  列 9 至 11

  -3.359567595262150  -3.163846322248371  -2.909301945209178
   1.658345996992094   2.254344113727377   2.832228784247623
   5.998275203244931   5.895390485630893   5.637213316282446

>> error

error =

   1.0e-04 *

  列 1 至 8

                   0  -0.034974617277861  -0.067580482339125  -0.094496964977431  -0.112720723053350  -0.119765782056191  -0.113835856074829  -0.093959152320799

  列 9 至 11

  -0.060077793553326  -0.013086298240594   0.045183834957996